人教版(新)九上-22.3实际问题与二次函数 第三课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-22.3实际问题与二次函数 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览








文档简介
(共33张PPT)
22.3实际问题
与二次函数
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前面我们已经学习了利用二次函数解决几何最值问题,实际问题中最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
新课精讲
探索新知
1
知识点
实际中二次函数模型的建立
我们先来学习利用二次函数.
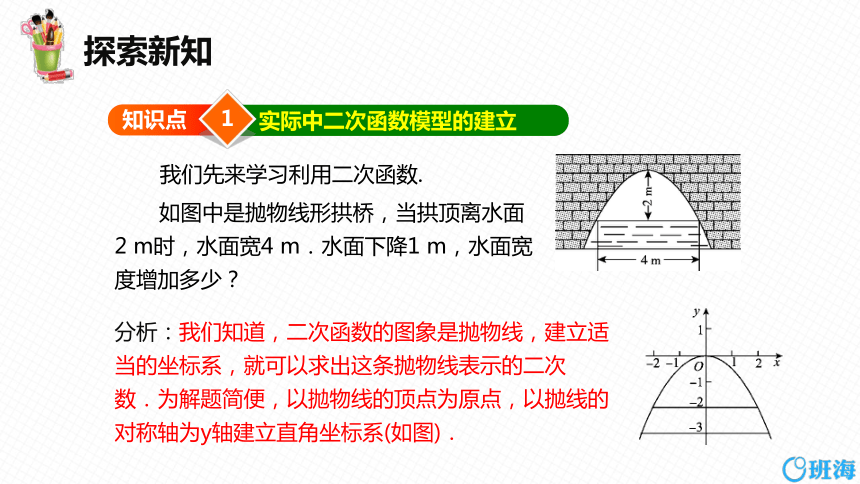
如图中是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m.水面下降1 m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次数.为解题简便,以拋物线的顶点为原点,以抛线的对称轴为y轴建立直角坐标系(如图).
探索新知
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=- x2.
当水面下降1 m时,水面的纵坐标为-3.请你根据上面的函数解析式求出这时的水面宽度.
当y=-3时,- x2=-3,解得x1= ,x2=- (舍去).
所以当水面下降1 m时,水面宽度为 m.
水面下降1 m,水面宽度增加________m.
探索新知
归 纳
解决抛物线型建筑问题“三步骤”:
1.根据题意,建立恰当的坐标系,设抛物线解析式;
2.准确转化线段的长与点的坐标之间的关系,得到抛物线上点的坐标,代入解析式,求出二次函数解析式;
3.应用所求解析式及性质解决问题.
典题精讲
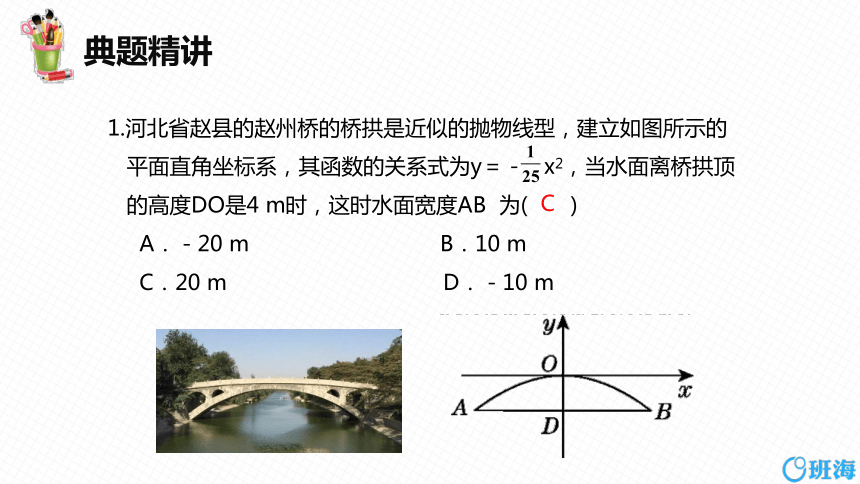
1.河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如图所示的
平面直角坐标系,其函数的关系式为y=- x2,当水面离桥拱顶
的高度DO是4 m时,这时水面宽度AB 为( )
A.-20 m B.10 m
C.20 m D.-10 m
C
典题精讲
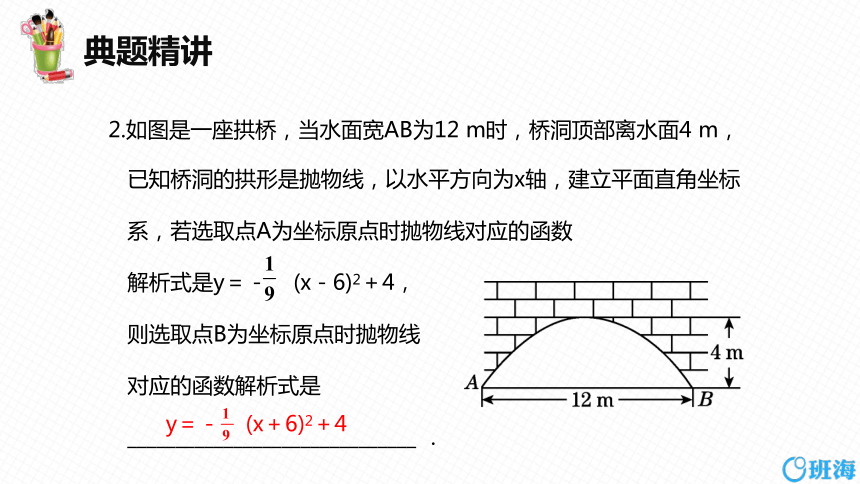
2.如图是一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,
已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标
系,若选取点A为坐标原点时抛物线对应的函数
解析式是y=- (x-6)2+4,
则选取点B为坐标原点时抛物线
对应的函数解析式是
______________________________ .
y=- (x+6)2+4
探索新知
2
知识点
求实际中“抛物线”型的最值问题
前面我们已学习了利用二次函数解决抛物线型建筑问题,下面我们学习建立坐标系解抛物线型运动问题.
探索新知
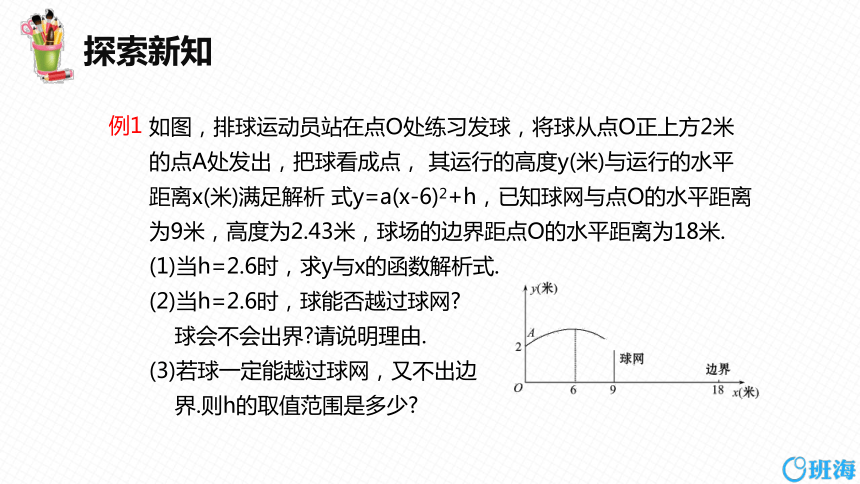
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出,把球看成点, 其运行的高度y(米)与运行的水平距离x(米)满足解析 式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数解析式.
(2)当h=2.6时,球能否越过球网
球会不会出界 请说明理由.
(3)若球一定能越过球网,又不出边
界.则h的取值范围是多少
例1
探索新知
(1)利用h=2.6,球从O点正上方2m的A处发出,将点(0, 2)代入解析
式求出即可.
(2)利用当x=9时,y=- (x-6)2+2.6=2.45,
当y=0 时,- (x-6)2+2.6=0,分别得出结果.
(3)根据当球正好过点(18,0)时,抛物线y=a(x-6)2+h还过点(0, 2),
以及当球刚能过网, 此时函数图象过(9, 2.43),抛物线
y=a(x-6)2+h 还过点(0, 2)时分别得出h的取值范围,即可得出答案.
思路点拨:
探索新知
(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x-6)2+h过点(0, 2),
∴2=a(0-6)2+2.6,解得:a= - ,
故y与x的函数解析式为 y= - (x-6)2+2.6.
(2)当x=9时, y=- (x-6)2+2.6=2.45>2.43,所以球能过球网;
当y=0时, - (x-6)2+2.6=0,
解得: x1=6+2 >18, x2=6-2 (舍去),故会出界.
解:
探索新知
(3)当球正好过点(18,0)时,抛物线y=a(x-6)2+h还过点(0,2),
代入解析式得
此时二次函数解析式为y=- (x-6)2+ ,
此时球若不出边界,则h≥ ;当球刚能过网,此时函数图象过(9,2.43),
抛物线y=a(x-6)2+h 还过点(0,2),代入解析式得
此时球要过网,则h≥ ,
故若球一定能越过球网,又不出边界,h的取值范围是:h≥ .
探索新知
归 纳
解决抛物线型运动问题时,要会根据图的特点,建立恰当的坐标系,由抛物线图象读出最大高度和最远距离(一般以水平面为x轴),然后借助抛物线上一些特殊点的坐标求出函数解析式,并解决问题.
典题精讲
1.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水
点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=
-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.5米 C.6米 D.7米
A
2.向上发射一枚炮弹,经x秒后的高度为y米,且时间与高度关系为y=
ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个
时间的高度是最高的( )
A.第9.5秒 B.第10秒
C.第10.5秒 D.第11秒
C
学以致用
小试牛刀
1.在解决形状是抛物线(抛物线形状的拱桥、物体的运动路线等)的实
际问题时,通常需要建立适当的_________________.为方便解决问
题,通常以抛物线的顶点为__________,此抛物线的对称轴为_____
建立平面直角坐标系.
平面直角坐标系
坐标原点
y轴
2.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函
数解析式是s=60t- t2,则飞机着陆后滑行的最长时间为_____.
20 s
小试牛刀
3.如图是一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度
为4 m;那么当水位下降
1 m后,水面的宽度为_____.
4.有一拱桥呈抛物线形状,这个桥洞的最大高度是16 m,跨度为40
m,现把它的示意图(如图)放在平面直角坐标系中,则抛物线对应
的函数解析式为( )
A.y= x2+ x B.y=- x2- x
C.y=- x2+ x D.y=- x2+ x+16
C
小试牛刀
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线
是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与
足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对
称轴是直线t= ;③足球被踢出9 s时落地;④足球被踢出1.5 s时,
距离地面的高度是11 m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
B
小试牛刀
6.如图,某灌溉设备的喷头B高出地面1.25 m,喷出的抛物线型水流在
与喷头底部A的水平距离为1 m处达到距离地面最大
高度2.25 m,试建立恰当的平面直角坐标系并求出
与该抛物线型水流对应的二次函数解析式.
(1)以抛物线型水流顶点为坐标原点建立平面直角坐标系的函数解析式
为____________;
y=-x2
(2)从抛物线型水流顶点向地面作垂线,得到垂足,以该垂足为坐标原
点建立平面直角坐标系的函数解析式为________________;
y=-x2+2.25
(3)以点A为坐标原点建立平面直角坐标系的函数解析式为
_____________________________________________________.
y=-(x-1)2+2.25或y=-x2+2x+1.25
小试牛刀
7.如图,隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽
是4 m.按照图中所示的直角坐标系,抛物线可以用y=- x2+bx+c
表示,且抛物线上的点C到墙面OB的水平距离为3 m,到地面OA的
距离为172 m.
(1)求该抛物线对应的函数解析
式,并计算出拱顶D到地面
OA的距离.
小试牛刀
解:(1)根据题意得B(0,4),C(3, ). 把点B(0,4),C(3, )的
坐标分别代入y=-16x2+bx+c,
所以抛物线对应的函数解析式为y=-16x2+2x+4,
即y=-16(x-6)2+10.
所以D点的坐标为(6,10).
所以拱顶D到地面OA的距离为10 m.
得
解得
小试牛刀
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧
道内设双向行车道,那么这辆货运汽车能否安全通过?
由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= >6,
所以这辆货运汽车能安全通过.
小试牛刀
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,
如果灯离地面的高度不超过8 m,那么两排灯的水平距离最小是
多少米?
令y=8,则-16(x-6)2+10=8,
解得x1=6+ ,x2=6- ,
则x1-x2= .
所以两排灯的水平距离最小是 m.
小试牛刀
8.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部
分.如图,甲在O点正上方1 m的P处发出一球,羽毛球飞行的高
度y(m)与水平距离x(m)之间满足函数解析式y=a(x-4)2+h,已
知点O与球网的水平距离为5 m,球网的高度为1.55 m.
(1)当a=- 时,①求h的值;
②通过计算判断此球能否过网.
小试牛刀
解:①当a=- 时,
函数解析式为y=- (x-4)2+h.
∵P(0,1),∴1=- ×(0-4)2+h,解得h= .
②当x=5时,y=- ×(5-4)2+ = =1.625>1.55,
∴此球能过网.
小试牛刀
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7 m,离地面的
高度为125 m的Q处时,乙扣球成功,求a的值.
∵P(0,1),Q(7, ),
∴
解得
∴a的值为-15.
课堂小结
课堂小结
1.抛物线型建筑物问题:
几种常见的抛物线型建筑 物有拱形桥洞、隧道洞口、拱形门等.解决这类 问题的关键是根据已知条件选择合理的位置建立 直角坐标系,结合问题中的数据求出函数解析式, 然后利用函数解析式解决问题.
2.运动问题:
(1)运动中的距离、时间、速度问题;这类问题多根据运动规律中的公式求解.
(2)物体的运动路线(轨迹)问题;解决这类问题的思想方法是利用数形结合思想和函数思想,合理建立直角坐标系,根据已知数据,运用待定系数法求出运动轨迹(抛物线)的解析式,再利用二次函数的性质去分析、解决问题.
课堂小结
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.3实际问题
与二次函数
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前面我们已经学习了利用二次函数解决几何最值问题,实际问题中最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
新课精讲
探索新知
1
知识点
实际中二次函数模型的建立
我们先来学习利用二次函数.
如图中是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m.水面下降1 m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次数.为解题简便,以拋物线的顶点为原点,以抛线的对称轴为y轴建立直角坐标系(如图).
探索新知
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=- x2.
当水面下降1 m时,水面的纵坐标为-3.请你根据上面的函数解析式求出这时的水面宽度.
当y=-3时,- x2=-3,解得x1= ,x2=- (舍去).
所以当水面下降1 m时,水面宽度为 m.
水面下降1 m,水面宽度增加________m.
探索新知
归 纳
解决抛物线型建筑问题“三步骤”:
1.根据题意,建立恰当的坐标系,设抛物线解析式;
2.准确转化线段的长与点的坐标之间的关系,得到抛物线上点的坐标,代入解析式,求出二次函数解析式;
3.应用所求解析式及性质解决问题.
典题精讲
1.河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如图所示的
平面直角坐标系,其函数的关系式为y=- x2,当水面离桥拱顶
的高度DO是4 m时,这时水面宽度AB 为( )
A.-20 m B.10 m
C.20 m D.-10 m
C
典题精讲
2.如图是一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,
已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标
系,若选取点A为坐标原点时抛物线对应的函数
解析式是y=- (x-6)2+4,
则选取点B为坐标原点时抛物线
对应的函数解析式是
______________________________ .
y=- (x+6)2+4
探索新知
2
知识点
求实际中“抛物线”型的最值问题
前面我们已学习了利用二次函数解决抛物线型建筑问题,下面我们学习建立坐标系解抛物线型运动问题.
探索新知
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出,把球看成点, 其运行的高度y(米)与运行的水平距离x(米)满足解析 式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数解析式.
(2)当h=2.6时,球能否越过球网
球会不会出界 请说明理由.
(3)若球一定能越过球网,又不出边
界.则h的取值范围是多少
例1
探索新知
(1)利用h=2.6,球从O点正上方2m的A处发出,将点(0, 2)代入解析
式求出即可.
(2)利用当x=9时,y=- (x-6)2+2.6=2.45,
当y=0 时,- (x-6)2+2.6=0,分别得出结果.
(3)根据当球正好过点(18,0)时,抛物线y=a(x-6)2+h还过点(0, 2),
以及当球刚能过网, 此时函数图象过(9, 2.43),抛物线
y=a(x-6)2+h 还过点(0, 2)时分别得出h的取值范围,即可得出答案.
思路点拨:
探索新知
(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x-6)2+h过点(0, 2),
∴2=a(0-6)2+2.6,解得:a= - ,
故y与x的函数解析式为 y= - (x-6)2+2.6.
(2)当x=9时, y=- (x-6)2+2.6=2.45>2.43,所以球能过球网;
当y=0时, - (x-6)2+2.6=0,
解得: x1=6+2 >18, x2=6-2 (舍去),故会出界.
解:
探索新知
(3)当球正好过点(18,0)时,抛物线y=a(x-6)2+h还过点(0,2),
代入解析式得
此时二次函数解析式为y=- (x-6)2+ ,
此时球若不出边界,则h≥ ;当球刚能过网,此时函数图象过(9,2.43),
抛物线y=a(x-6)2+h 还过点(0,2),代入解析式得
此时球要过网,则h≥ ,
故若球一定能越过球网,又不出边界,h的取值范围是:h≥ .
探索新知
归 纳
解决抛物线型运动问题时,要会根据图的特点,建立恰当的坐标系,由抛物线图象读出最大高度和最远距离(一般以水平面为x轴),然后借助抛物线上一些特殊点的坐标求出函数解析式,并解决问题.
典题精讲
1.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水
点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=
-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.5米 C.6米 D.7米
A
2.向上发射一枚炮弹,经x秒后的高度为y米,且时间与高度关系为y=
ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个
时间的高度是最高的( )
A.第9.5秒 B.第10秒
C.第10.5秒 D.第11秒
C
学以致用
小试牛刀
1.在解决形状是抛物线(抛物线形状的拱桥、物体的运动路线等)的实
际问题时,通常需要建立适当的_________________.为方便解决问
题,通常以抛物线的顶点为__________,此抛物线的对称轴为_____
建立平面直角坐标系.
平面直角坐标系
坐标原点
y轴
2.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函
数解析式是s=60t- t2,则飞机着陆后滑行的最长时间为_____.
20 s
小试牛刀
3.如图是一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度
为4 m;那么当水位下降
1 m后,水面的宽度为_____.
4.有一拱桥呈抛物线形状,这个桥洞的最大高度是16 m,跨度为40
m,现把它的示意图(如图)放在平面直角坐标系中,则抛物线对应
的函数解析式为( )
A.y= x2+ x B.y=- x2- x
C.y=- x2+ x D.y=- x2+ x+16
C
小试牛刀
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线
是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与
足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对
称轴是直线t= ;③足球被踢出9 s时落地;④足球被踢出1.5 s时,
距离地面的高度是11 m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
B
小试牛刀
6.如图,某灌溉设备的喷头B高出地面1.25 m,喷出的抛物线型水流在
与喷头底部A的水平距离为1 m处达到距离地面最大
高度2.25 m,试建立恰当的平面直角坐标系并求出
与该抛物线型水流对应的二次函数解析式.
(1)以抛物线型水流顶点为坐标原点建立平面直角坐标系的函数解析式
为____________;
y=-x2
(2)从抛物线型水流顶点向地面作垂线,得到垂足,以该垂足为坐标原
点建立平面直角坐标系的函数解析式为________________;
y=-x2+2.25
(3)以点A为坐标原点建立平面直角坐标系的函数解析式为
_____________________________________________________.
y=-(x-1)2+2.25或y=-x2+2x+1.25
小试牛刀
7.如图,隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽
是4 m.按照图中所示的直角坐标系,抛物线可以用y=- x2+bx+c
表示,且抛物线上的点C到墙面OB的水平距离为3 m,到地面OA的
距离为172 m.
(1)求该抛物线对应的函数解析
式,并计算出拱顶D到地面
OA的距离.
小试牛刀
解:(1)根据题意得B(0,4),C(3, ). 把点B(0,4),C(3, )的
坐标分别代入y=-16x2+bx+c,
所以抛物线对应的函数解析式为y=-16x2+2x+4,
即y=-16(x-6)2+10.
所以D点的坐标为(6,10).
所以拱顶D到地面OA的距离为10 m.
得
解得
小试牛刀
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧
道内设双向行车道,那么这辆货运汽车能否安全通过?
由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= >6,
所以这辆货运汽车能安全通过.
小试牛刀
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,
如果灯离地面的高度不超过8 m,那么两排灯的水平距离最小是
多少米?
令y=8,则-16(x-6)2+10=8,
解得x1=6+ ,x2=6- ,
则x1-x2= .
所以两排灯的水平距离最小是 m.
小试牛刀
8.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部
分.如图,甲在O点正上方1 m的P处发出一球,羽毛球飞行的高
度y(m)与水平距离x(m)之间满足函数解析式y=a(x-4)2+h,已
知点O与球网的水平距离为5 m,球网的高度为1.55 m.
(1)当a=- 时,①求h的值;
②通过计算判断此球能否过网.
小试牛刀
解:①当a=- 时,
函数解析式为y=- (x-4)2+h.
∵P(0,1),∴1=- ×(0-4)2+h,解得h= .
②当x=5时,y=- ×(5-4)2+ = =1.625>1.55,
∴此球能过网.
小试牛刀
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7 m,离地面的
高度为125 m的Q处时,乙扣球成功,求a的值.
∵P(0,1),Q(7, ),
∴
解得
∴a的值为-15.
课堂小结
课堂小结
1.抛物线型建筑物问题:
几种常见的抛物线型建筑 物有拱形桥洞、隧道洞口、拱形门等.解决这类 问题的关键是根据已知条件选择合理的位置建立 直角坐标系,结合问题中的数据求出函数解析式, 然后利用函数解析式解决问题.
2.运动问题:
(1)运动中的距离、时间、速度问题;这类问题多根据运动规律中的公式求解.
(2)物体的运动路线(轨迹)问题;解决这类问题的思想方法是利用数形结合思想和函数思想,合理建立直角坐标系,根据已知数据,运用待定系数法求出运动轨迹(抛物线)的解析式,再利用二次函数的性质去分析、解决问题.
课堂小结
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
