人教版(新)九上-22.3实际问题与二次函数 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-22.3实际问题与二次函数 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
22.3实际问题
与二次函数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
对于某些实际问题,如果其中变量之间的关系可以用二次函数模型来刻画,那么我们就可以利用二次函数的图象和性质来研究.
新课精讲
探索新知
1
知识点
二次函数的最值
问 题
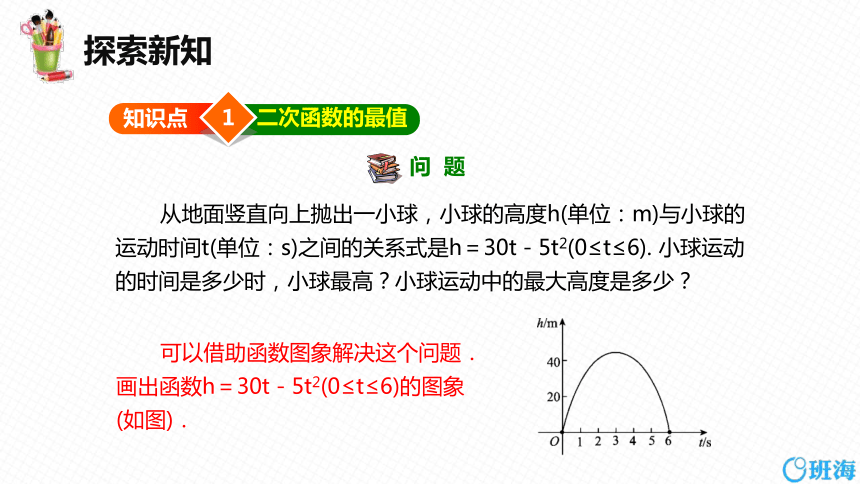
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6). 小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
可以借助函数图象解决这个问题.
画出函数h=30t-5t2(0≤t≤6)的图象
(如图).
探索新知
可以看出,这个函数的图象是一条抛物线的一部分.这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值.因此,当t= 时,h有最大值 也就是说,小球运动的时间是3 s时,小球最高.小球运动中的最大高度是45 m.
探索新知
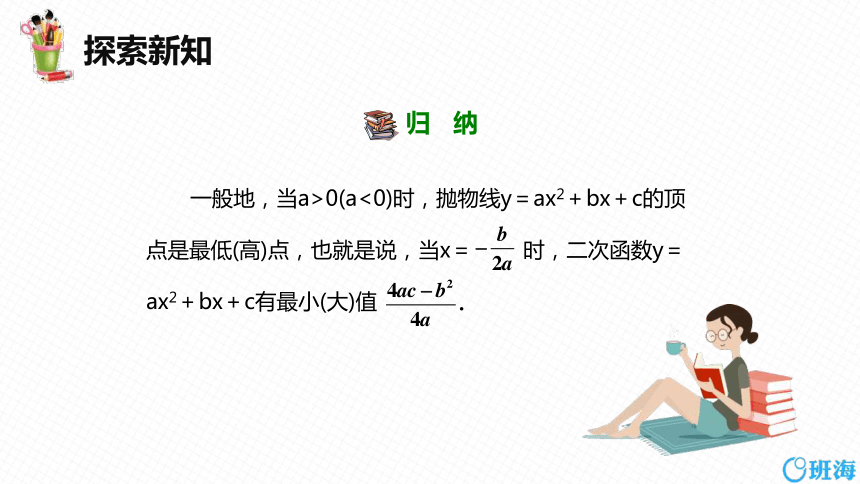
归 纳
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值
典题精讲
二次函数y=x2-4x+c的最小值为0,则c的值为( )
A.2
B.4
C.-4
D.16
C
探索新知
2
知识点
图形的最值
例1 总长为60 m的篱笆围成矩形场地,矩形面积S随矩形一边长l
的变化而变化,当l是多少米时,场地的面积S最大?
分析:先写出S关于l的函数解析式,再求出使S最大的l值.
探索新知
矩形场地的周长是60 m,一边长为l m,
所以另一边长为 m.
场地的面积S=l(30-l),
即S=-l2+30l(0因此,当l= 时,
S有最大值
也就是说,当l是15 m时,场地的面积S最大.
解:
探索新知
总 结
在周长一定的情况下,所围成的几何图形的形状不同, 所得到的几
何图形的面积也不同.利用二次函数求几何图形的最大(小)面积的一般
步骤:
(1)引入自变量,用含自变量的代数式分别表示与所求问题相关的量.
(2)分析题目中的数量关系,根据题意列出函数解析式.
(3)根据函数解析式求出最值及取得最值时自变量的值,注意自变量的
取值范围.
典题精讲
2.用一条长为40 cm的绳子围成一个面积为a cm2的长方形,a的值不
可能为( )
A.20 B.40 C.100 D.120
1.已知一个直角三角形两直角边长之和为20 cm则这个直角三角形的
最大面积为( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
B
D
学以致用
小试牛刀
1.一般地,当a>0(或a<0)时,抛物线y=ax2+bx+c的顶点是________
(或最高)点,即当x=________时,二次函数y=ax2+bx+c有_______
(或最大)值____________.
最低
最小
2.利用二次函数求图形面积的最值时,先构建二次函数模型,利用图
形的相关性质及相等关系求出_________的解析式,并写出________
的取值范围,再利用二次函数的性质求出图形面积的最值.
二次函数
自变量
小试牛刀
3.实际问题中求最值的一般步骤:
(1)分析问题中的____________;
(2)列出______________;
(3)根据函数解析式的最值情况,结合实际,解决问题.
数量关系
函数解析式
4.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,为了使
一天出售该种手工艺品的总利润y(元)最大,则x的值为( )
A.4 B.5
C.6 D.8
A
小试牛刀
5.某商店销售皮鞋,已知所获利润y(元)与销售单价x(元)之间的关系式
为y=-x2+24x+2 956,则获利最多为( )
A.3 144元 B.3 100元
C.144元 D.2 956元
B
6.二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,
最大值为2n,则m+n的值为( )
A. B.2
C. D.
D
小试牛刀
7.已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,
下列说法正确的是( )
A.有最小值-5,最大值0
B.有最小值-3,最大值6
C.有最小值0,最大值6
D.有最小值2,最大值6
B
小试牛刀
8.在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10 m,
拴住小狗的10 m长的绳子一端固定在B点处,小狗在不能进入小屋
内的条件下活动,其可以活动的区
域面积为S(m2).
(1)如图①,若BC=4 m,
则S=________;
88π m2
小试牛刀
(2)如图②,现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一等
边三角形CDE区域,使之变成落地为五边形ABCED的小屋,其他
条件不变,则在BC的变化过程中,
当S取得最小值时,边BC的长
为______.
小试牛刀
9.工人师傅用一块长为10 dm,宽为6 dm的矩形铁皮制作一个无盖的
长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)在图中画出裁剪示意图,用实线表示裁剪线,
虚线表示折痕;并求长方体底面面积为12 dm2
时,裁掉的正方形边长多大?
如图:设裁掉的正方形的边长为x dm,
由题意可得(10-2x)(6-2x)=12,
即x2-8x+12=0,
解得x=2或x=6(不合题意,舍去).答:裁掉的正方形的边长为2 dm.
小试牛刀
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈
处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,
裁掉的正方形边长多大时,总费用最低,最低为多少?
根据题意,得10-2x≤5(6-2x),解得x≤2.5,∵x>0,∴0<x≤2.5.
设总费用为w元,由题意可知
w=0.5×2x(16-4x)+2(10-2x)(6-2x)=4x2-48x+120=4(x-6)2-24,
∴当0<x≤2.5时,w随x的增大而减小,
∴当x=2.5时,w有最小值,最小值为25.
答:当裁掉边长为2.5 dm的正方形时,总费用最低,最低费用为25元.
课堂小结
课堂小结
1.怎样求二次函数的最大(小)值?
2.求几何图形面积的最值时都有哪些步骤?
(1)引入自变量,用含自变量的代数式分别表示与所求题相关的量.
(2)分析题目中的数量关系,根据题意列出函数解析式.
(3)根据函数解析式求出最值及取得最值时自变量的值,注意自变量的
取值范围.
当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.3实际问题
与二次函数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
对于某些实际问题,如果其中变量之间的关系可以用二次函数模型来刻画,那么我们就可以利用二次函数的图象和性质来研究.
新课精讲
探索新知
1
知识点
二次函数的最值
问 题
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6). 小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
可以借助函数图象解决这个问题.
画出函数h=30t-5t2(0≤t≤6)的图象
(如图).
探索新知
可以看出,这个函数的图象是一条抛物线的一部分.这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值.因此,当t= 时,h有最大值 也就是说,小球运动的时间是3 s时,小球最高.小球运动中的最大高度是45 m.
探索新知
归 纳
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值
典题精讲
二次函数y=x2-4x+c的最小值为0,则c的值为( )
A.2
B.4
C.-4
D.16
C
探索新知
2
知识点
图形的最值
例1 总长为60 m的篱笆围成矩形场地,矩形面积S随矩形一边长l
的变化而变化,当l是多少米时,场地的面积S最大?
分析:先写出S关于l的函数解析式,再求出使S最大的l值.
探索新知
矩形场地的周长是60 m,一边长为l m,
所以另一边长为 m.
场地的面积S=l(30-l),
即S=-l2+30l(0
S有最大值
也就是说,当l是15 m时,场地的面积S最大.
解:
探索新知
总 结
在周长一定的情况下,所围成的几何图形的形状不同, 所得到的几
何图形的面积也不同.利用二次函数求几何图形的最大(小)面积的一般
步骤:
(1)引入自变量,用含自变量的代数式分别表示与所求问题相关的量.
(2)分析题目中的数量关系,根据题意列出函数解析式.
(3)根据函数解析式求出最值及取得最值时自变量的值,注意自变量的
取值范围.
典题精讲
2.用一条长为40 cm的绳子围成一个面积为a cm2的长方形,a的值不
可能为( )
A.20 B.40 C.100 D.120
1.已知一个直角三角形两直角边长之和为20 cm则这个直角三角形的
最大面积为( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
B
D
学以致用
小试牛刀
1.一般地,当a>0(或a<0)时,抛物线y=ax2+bx+c的顶点是________
(或最高)点,即当x=________时,二次函数y=ax2+bx+c有_______
(或最大)值____________.
最低
最小
2.利用二次函数求图形面积的最值时,先构建二次函数模型,利用图
形的相关性质及相等关系求出_________的解析式,并写出________
的取值范围,再利用二次函数的性质求出图形面积的最值.
二次函数
自变量
小试牛刀
3.实际问题中求最值的一般步骤:
(1)分析问题中的____________;
(2)列出______________;
(3)根据函数解析式的最值情况,结合实际,解决问题.
数量关系
函数解析式
4.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,为了使
一天出售该种手工艺品的总利润y(元)最大,则x的值为( )
A.4 B.5
C.6 D.8
A
小试牛刀
5.某商店销售皮鞋,已知所获利润y(元)与销售单价x(元)之间的关系式
为y=-x2+24x+2 956,则获利最多为( )
A.3 144元 B.3 100元
C.144元 D.2 956元
B
6.二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,
最大值为2n,则m+n的值为( )
A. B.2
C. D.
D
小试牛刀
7.已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,
下列说法正确的是( )
A.有最小值-5,最大值0
B.有最小值-3,最大值6
C.有最小值0,最大值6
D.有最小值2,最大值6
B
小试牛刀
8.在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10 m,
拴住小狗的10 m长的绳子一端固定在B点处,小狗在不能进入小屋
内的条件下活动,其可以活动的区
域面积为S(m2).
(1)如图①,若BC=4 m,
则S=________;
88π m2
小试牛刀
(2)如图②,现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一等
边三角形CDE区域,使之变成落地为五边形ABCED的小屋,其他
条件不变,则在BC的变化过程中,
当S取得最小值时,边BC的长
为______.
小试牛刀
9.工人师傅用一块长为10 dm,宽为6 dm的矩形铁皮制作一个无盖的
长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)在图中画出裁剪示意图,用实线表示裁剪线,
虚线表示折痕;并求长方体底面面积为12 dm2
时,裁掉的正方形边长多大?
如图:设裁掉的正方形的边长为x dm,
由题意可得(10-2x)(6-2x)=12,
即x2-8x+12=0,
解得x=2或x=6(不合题意,舍去).答:裁掉的正方形的边长为2 dm.
小试牛刀
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈
处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,
裁掉的正方形边长多大时,总费用最低,最低为多少?
根据题意,得10-2x≤5(6-2x),解得x≤2.5,∵x>0,∴0<x≤2.5.
设总费用为w元,由题意可知
w=0.5×2x(16-4x)+2(10-2x)(6-2x)=4x2-48x+120=4(x-6)2-24,
∴当0<x≤2.5时,w随x的增大而减小,
∴当x=2.5时,w有最小值,最小值为25.
答:当裁掉边长为2.5 dm的正方形时,总费用最低,最低费用为25元.
课堂小结
课堂小结
1.怎样求二次函数的最大(小)值?
2.求几何图形面积的最值时都有哪些步骤?
(1)引入自变量,用含自变量的代数式分别表示与所求题相关的量.
(2)分析题目中的数量关系,根据题意列出函数解析式.
(3)根据函数解析式求出最值及取得最值时自变量的值,注意自变量的
取值范围.
当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
