人教版(新)九上-23.1 图形的旋转 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-23.1 图形的旋转 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览









文档简介
(共31张PPT)
23.1 图形的旋转
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同学们都见过风车吧,它能在风的吹动下不停地转动.在我们周围,还能看到许多转动着的物体,如车轮、水车、风力发电机、飞机的螺旋桨、时钟的指针、游乐园的大转盘……我们就生活在一个处处能见到旋转现象的世界中.
在数学中,旋转是图形变化的方法之一,应该怎样描述它呢?它又有什么性质呢?本章将解答这些问题.
让我们一起来探索旋转的奥秘吧!
新课精讲
探索新知
1
知识点
旋转及相关概念
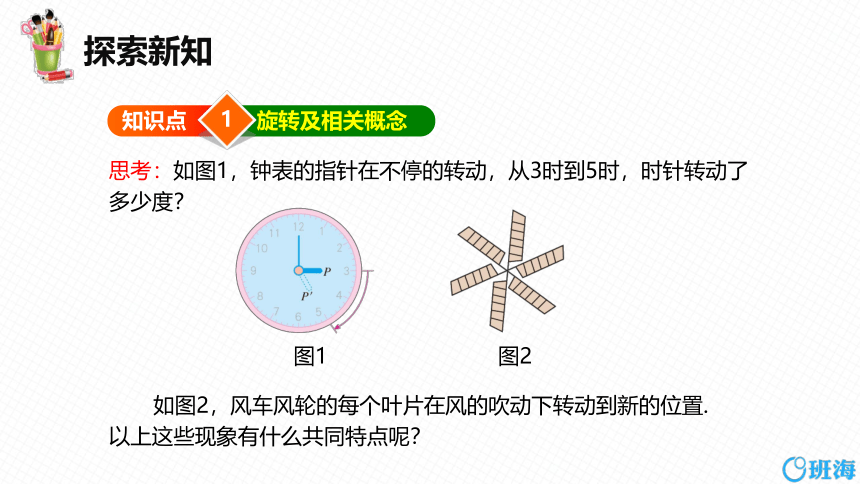
思考:如图1,钟表的指针在不停的转动,从3时到5时,时针转动了多少度?
如图2,风车风轮的每个叶片在风的吹动下转动到新的位置.
以上这些现象有什么共同特点呢?
图1
图2
探索新知
探索新知
(1)旋转中心在旋转的过程中是静止不动的,旋转中心可以在图形的外部,也可以在图形的内部,还可以在图形上.
(2)将一个图形绕一个定点沿某个方向转动一个角度,意味着图形上每一个点同时按相同方向旋转相同的角度.
(3)旋转的三要素:旋转中心,旋转角,旋转方向.
探索新知
例1 下列运动属于旋转的是( )
A.篮球的滚动
B.钟摆的摆动
C.气球升空的运动
D.一个图形沿某条直线对折的过程
导引:按旋转的定义判断.
B
探索新知
总 结
判断一种运动是否是旋转的前提条件是图形在同一平面内的运动,其次要紧扣旋转的“三要素”,看是否同时具有:旋转中心,旋转角度,旋转方向.
探索新知
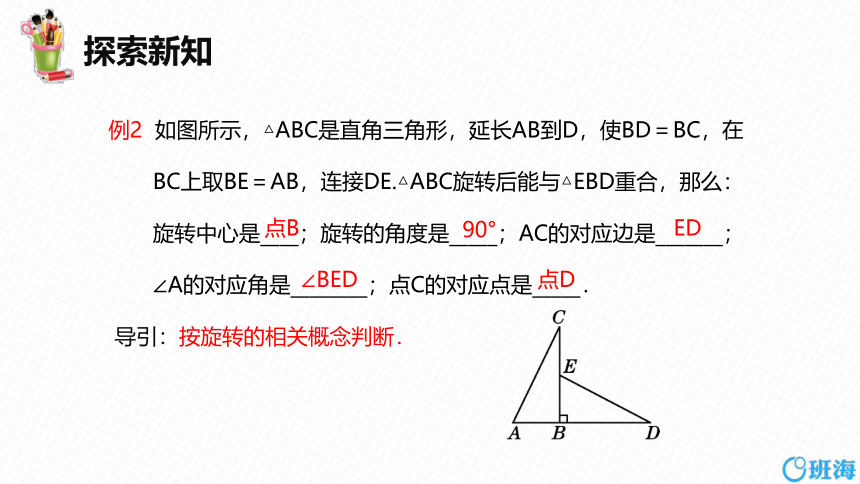
例2 如图所示,△ABC是直角三角形,延长AB到D,使BD=BC,在
BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:
旋转中心是____;旋转的角度是_____;AC的对应边是_______;
∠A的对应角是________;点C的对应点是_____.
导引:按旋转的相关概念判断.
90°
点B
ED
∠BED
点D
探索新知
总 结
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
典题精讲
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
D
探索新知
2
知识点
旋转的性质
探究:如图,在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸
板,再描出这个挖掉的三角形(△ A′B′C′),
移开硬纸板.△A′B′C′是由△ABC绕点O旋转得到的.
线段OA与OA′有什么关系?∠AOA′与∠BOB′有
什么关系?△ABC与△ A′B′C′ 的形状和大小有
什么关系?
探索新知
探索新知
A
B
C
B′
C′
0
A
B
C
·
A′
B′
C′
旋转前、后的图形全等
即对应角相等,对应边相等.
对应点到旋转中心的距离相等。
探索新知
例3 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由
△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′
与点C是对应点),连接CC′,则∠ CC′ B′ 的度数是( )
A.45° B.30° C.25° D.15°
D
由旋转中心为点A,点C与点C′为对应点可知AC=AC′,又由∠CAC′=90°可知△CAC′为等腰直角三角形,所以∠ CC′ A= 45°.又由∠ AC′ B′ =∠ACB=90°-60°=30°,可得∠ CC′ B′ =15°.
解析 :
探索新知
总 结
(1)图形旋转时,图形中的每一个点都绕着旋转中心旋转
了同样大小的角度;
(2)旋转前后的图形的大小、形状都没有发生变化,只改
变了位置;
(3)旋转前后的对应线段相等、对应角相等.
典题精讲
1.如图,将等边三角形ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是( )
A.0
B.1
C.2
D.3
D
典题精讲
2.如图,在 ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于
∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,
∠ADA′=50°,则∠DA′E′的大小为( )
A.130°
B.150°
C.160°
D.170°
C
学以致用
小试牛刀
1.在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样
的图形运动叫做________,这个定点叫做____________,转动的角叫
做________角.
旋转
旋转中心
旋转
2.如图,△AOB绕着点O旋转至△A′OB′的位置,此时:
(1)点B的对应点是________;
(2)旋转中心是______,旋转角为
______________________;
(3)∠A的对应角是________,线段OB的对应线段是线段________.
点B′
点O
∠AOA′或∠BOB′
∠A′
OB′
小试牛刀
3.旋转的性质:(1)对应点到旋转中心的距离________;(2)任意一组对应
点与旋转中心的连线所成的角都等于____________; (3)旋转前、后的
图形________.
相等
旋转角
全等
4.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落
在AB的延长线上,连接AD.下列结论一定正确的是( )
A.∠ABD=∠E
B.∠CBE=∠C
C.AD∥BC
D.AD=BC
C
小试牛刀
5.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时
针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两
点间的距离为( )
A. B.2 C.3 D.2
A
6.将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,
得到数字“6”,现将数字“69”旋转180°,
得到的数字是( )
A.96 B.69 C.66 D.99
B
小试牛刀
7.如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变
换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以
是( )
A.△ABC绕点C顺时针旋转90°,
再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,
再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度
A
小试牛刀
8.如图,将△ABC绕点C顺时针方向旋转40°得到△A′B′C,若AC⊥A′B′,
则∠A等于( )
A.50°
B.60°
C.70°
D.80°
A
小试牛刀
9.如图,在Rt△ABC中,∠ACB=90°,点D,E
分别在AB,AC上,CE=BC,连接CD,将
线段CD绕点C按顺时针方向旋转90°后得CF,
连接EF.
(1)补充完成图形;
小试牛刀
(2)若EF∥CD,求证:∠BDC=90°.
证明:由旋转的性质得:∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°.
∵∠ACB=90°, ∴∠DCE+∠BCD=90°. ∴∠ECF=∠BCD.
∵EF∥DC, ∴∠EFC+∠DCF=180°. ∴∠EFC=90°,
在△BDC和△EFC中,
∴△BDC≌△EFC(SAS). ∴∠BDC=∠EFC=90°.
课堂小结
课堂小结
旋转
旋转三要素
旋转的定义
旋转的性质
旋转的相关概念
旋转中心、旋转方向、旋转角
旋转中心
旋转角
对应点
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
23.1 图形的旋转
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同学们都见过风车吧,它能在风的吹动下不停地转动.在我们周围,还能看到许多转动着的物体,如车轮、水车、风力发电机、飞机的螺旋桨、时钟的指针、游乐园的大转盘……我们就生活在一个处处能见到旋转现象的世界中.
在数学中,旋转是图形变化的方法之一,应该怎样描述它呢?它又有什么性质呢?本章将解答这些问题.
让我们一起来探索旋转的奥秘吧!
新课精讲
探索新知
1
知识点
旋转及相关概念
思考:如图1,钟表的指针在不停的转动,从3时到5时,时针转动了多少度?
如图2,风车风轮的每个叶片在风的吹动下转动到新的位置.
以上这些现象有什么共同特点呢?
图1
图2
探索新知
探索新知
(1)旋转中心在旋转的过程中是静止不动的,旋转中心可以在图形的外部,也可以在图形的内部,还可以在图形上.
(2)将一个图形绕一个定点沿某个方向转动一个角度,意味着图形上每一个点同时按相同方向旋转相同的角度.
(3)旋转的三要素:旋转中心,旋转角,旋转方向.
探索新知
例1 下列运动属于旋转的是( )
A.篮球的滚动
B.钟摆的摆动
C.气球升空的运动
D.一个图形沿某条直线对折的过程
导引:按旋转的定义判断.
B
探索新知
总 结
判断一种运动是否是旋转的前提条件是图形在同一平面内的运动,其次要紧扣旋转的“三要素”,看是否同时具有:旋转中心,旋转角度,旋转方向.
探索新知
例2 如图所示,△ABC是直角三角形,延长AB到D,使BD=BC,在
BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:
旋转中心是____;旋转的角度是_____;AC的对应边是_______;
∠A的对应角是________;点C的对应点是_____.
导引:按旋转的相关概念判断.
90°
点B
ED
∠BED
点D
探索新知
总 结
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
典题精讲
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
D
探索新知
2
知识点
旋转的性质
探究:如图,在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸
板,再描出这个挖掉的三角形(△ A′B′C′),
移开硬纸板.△A′B′C′是由△ABC绕点O旋转得到的.
线段OA与OA′有什么关系?∠AOA′与∠BOB′有
什么关系?△ABC与△ A′B′C′ 的形状和大小有
什么关系?
探索新知
探索新知
A
B
C
B′
C′
0
A
B
C
·
A′
B′
C′
旋转前、后的图形全等
即对应角相等,对应边相等.
对应点到旋转中心的距离相等。
探索新知
例3 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由
△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′
与点C是对应点),连接CC′,则∠ CC′ B′ 的度数是( )
A.45° B.30° C.25° D.15°
D
由旋转中心为点A,点C与点C′为对应点可知AC=AC′,又由∠CAC′=90°可知△CAC′为等腰直角三角形,所以∠ CC′ A= 45°.又由∠ AC′ B′ =∠ACB=90°-60°=30°,可得∠ CC′ B′ =15°.
解析 :
探索新知
总 结
(1)图形旋转时,图形中的每一个点都绕着旋转中心旋转
了同样大小的角度;
(2)旋转前后的图形的大小、形状都没有发生变化,只改
变了位置;
(3)旋转前后的对应线段相等、对应角相等.
典题精讲
1.如图,将等边三角形ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是( )
A.0
B.1
C.2
D.3
D
典题精讲
2.如图,在 ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于
∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,
∠ADA′=50°,则∠DA′E′的大小为( )
A.130°
B.150°
C.160°
D.170°
C
学以致用
小试牛刀
1.在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样
的图形运动叫做________,这个定点叫做____________,转动的角叫
做________角.
旋转
旋转中心
旋转
2.如图,△AOB绕着点O旋转至△A′OB′的位置,此时:
(1)点B的对应点是________;
(2)旋转中心是______,旋转角为
______________________;
(3)∠A的对应角是________,线段OB的对应线段是线段________.
点B′
点O
∠AOA′或∠BOB′
∠A′
OB′
小试牛刀
3.旋转的性质:(1)对应点到旋转中心的距离________;(2)任意一组对应
点与旋转中心的连线所成的角都等于____________; (3)旋转前、后的
图形________.
相等
旋转角
全等
4.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落
在AB的延长线上,连接AD.下列结论一定正确的是( )
A.∠ABD=∠E
B.∠CBE=∠C
C.AD∥BC
D.AD=BC
C
小试牛刀
5.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时
针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两
点间的距离为( )
A. B.2 C.3 D.2
A
6.将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,
得到数字“6”,现将数字“69”旋转180°,
得到的数字是( )
A.96 B.69 C.66 D.99
B
小试牛刀
7.如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变
换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以
是( )
A.△ABC绕点C顺时针旋转90°,
再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,
再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度
A
小试牛刀
8.如图,将△ABC绕点C顺时针方向旋转40°得到△A′B′C,若AC⊥A′B′,
则∠A等于( )
A.50°
B.60°
C.70°
D.80°
A
小试牛刀
9.如图,在Rt△ABC中,∠ACB=90°,点D,E
分别在AB,AC上,CE=BC,连接CD,将
线段CD绕点C按顺时针方向旋转90°后得CF,
连接EF.
(1)补充完成图形;
小试牛刀
(2)若EF∥CD,求证:∠BDC=90°.
证明:由旋转的性质得:∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°.
∵∠ACB=90°, ∴∠DCE+∠BCD=90°. ∴∠ECF=∠BCD.
∵EF∥DC, ∴∠EFC+∠DCF=180°. ∴∠EFC=90°,
在△BDC和△EFC中,
∴△BDC≌△EFC(SAS). ∴∠BDC=∠EFC=90°.
课堂小结
课堂小结
旋转
旋转三要素
旋转的定义
旋转的性质
旋转的相关概念
旋转中心、旋转方向、旋转角
旋转中心
旋转角
对应点
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
