人教版(新)九上-23.2.1 中心对称【优质课件】
文档属性
| 名称 | 人教版(新)九上-23.2.1 中心对称【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览









文档简介
(共39张PPT)
23.2.1 中心对称
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前面我们研究了旋转及其性质,现在研究一类特殊的旋转——中心对称及其性质.
新课精讲
探索新知
1
知识点
中心对称的定义
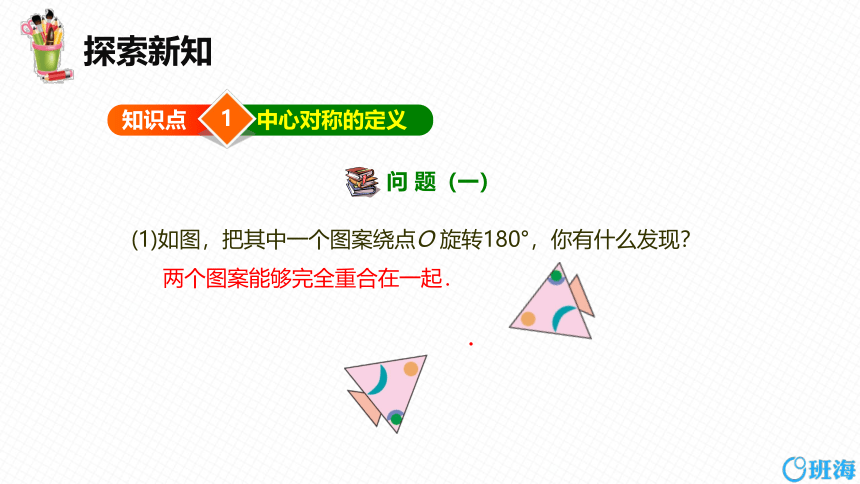
(1)如图,把其中一个图案绕点O 旋转180°,你有什么发现?
两个图案能够完全重合在一起.
问 题(一)
探索新知
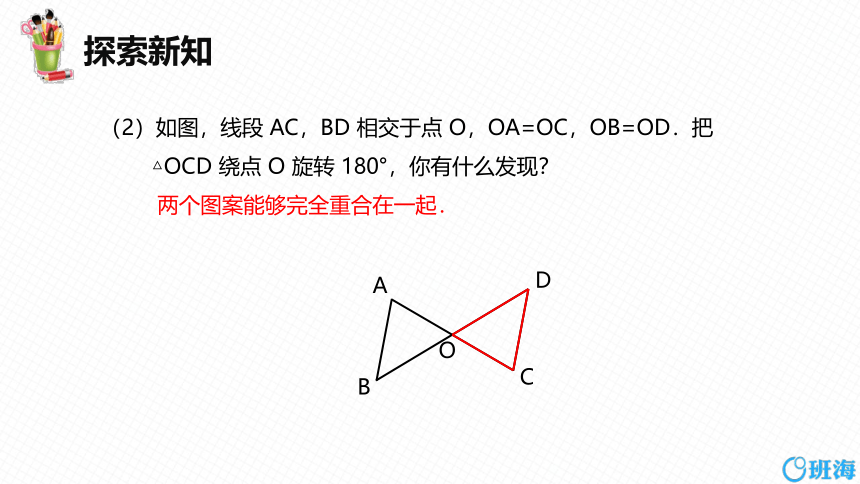
(2)如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把
△OCD 绕点 O 旋转 180°,你有什么发现?
两个图案能够完全重合在一起.
A
B
D
C
O
探索新知
你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
问 题(二)
点 O
180°
重合
探索新知
探索新知
例1 如图所示的图形中成中心对称的有________组.
导引:利用中心对称的定义解答.
3
探索新知
总 结
根据中心对称的定义,看左边的图形能否绕一点旋转180°后与右边的图形重合,能就成中心对称,否则就不成,本例中第四组不成.
典题精讲
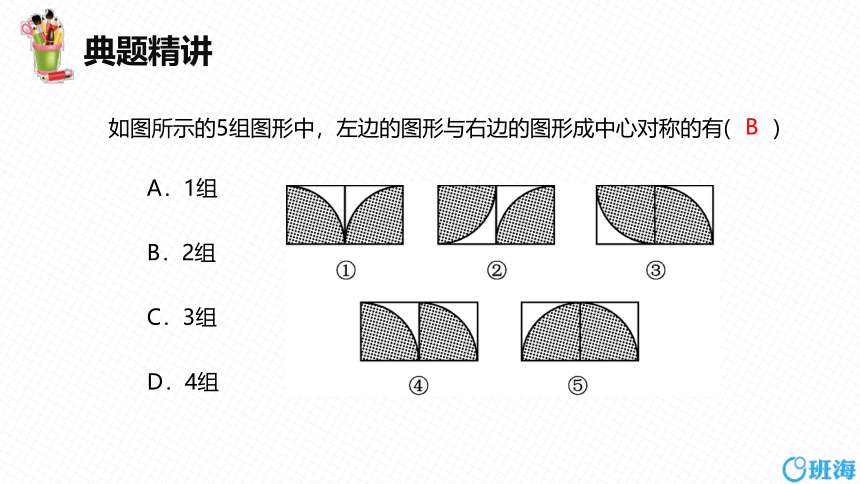
如图所示的5组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组
B.2组
C.3组
D.4组
B
探索新知
2
知识点
中心对称的性质
探 究
如图,旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A′B′C′;
第三步,移开三角板.
这样画出的△ABC 与△A′B′C′关于点O对称,分别连接对称点AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
C
A
B
C
A
B
A′
B′
O
C′
探索新知
我们可以发现:
(1)点O是线段AA′的中点.
(2)△ABC≌ △A′B′C′.
C
A
B
C′
A′
B′
O
探索新知
你能说明△ABC≌ △A′B′C′吗?
点A′是点A绕点O旋转180°得到的,
所以点O在线段AA′上,且OA=OA′,
同样地,点O也是线段BB′和CC′的中点.
在△AOB与△A′OB′中, OA=OA′,OB=OB′,AOB=∠A′OB′,
∴△AOB ≌ △ A′OB′. ∴AB=A′B′.
同理 BC=B′C′,AC=A′C′. ∴ △ABC ≌ △ A′B′C′.
C
A
B
C′
A′
B′
O
探索新知
探索新知
例2 如图,△A′B′C′与△ABC关于点O成中心对称,
你能从图中找出哪些相等的线段、相等的角、
全等的三角形以及有特殊位置关系的线段?
导引:根据中心对称的性质可知:如果两个图形关于某点成中心对
称,那么对称点所连线段都经过对称中心而且被对称中心平
分,而且这两个图形是全等图形,对应边平行(或共线)且相等.
解:可以找到:OA=OA′,OB=OB′,OC=OC′,△ABC≌ △A′B′C′,
AB A′B′,AC A′C′,BC B′C′,∠BAC=∠B′A′C′,
∠ABC=∠A′B′C′,∠ACB= ∠A′C′B′等.
探索新知
总 结
看准△ABC与△A′B′C′关于点O成中心对称的有关对称点,根据对称点来找对应线段、对应角,再由对称中心的性质得到对应线段的关系和对应角相等.
典题精讲
如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′. ED是△ABC
的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2
B.3
C.4
D.1.5
A
探索新知
3
知识点
中心对称的作图
我们已经掌握了中心对称定义和中心对称的性质. 下面我们要用所学的知识进行中心对称的作图.
探索新知
根据中心对称的性质作已知图形关于某点中心对称的图形的关键是作出某些特殊点的对称点.
作图步骤:
(1)连接原图形上的特殊点和对称中心;
(2)再将以上各线段延长找对称点,使得特殊点与对 称中心的距离和其对称点与对称中心的距离相等;
(3)将对称点按原图形的形状连接起来,即可得出原图形关于某点中心对称的图形.
探索新知
例3 (1)如图(1),选择点O为对称中心,画出点A关于点O的对
称点A′;
(2)如图(2),选择点O为对称中心,画出与△ABC关于点O
对称的△A′B′C′.
图(1)
图(2)
探索新知
(1)如图(3),连接AO,在AO的延长线上截取OA′=OA,即
可以求得点A关于点O的对称点A′.
(2)如图(4),作出A,B,C三点关于点O的对称点A′,B′,
C′,依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于点
O对称的△A′B′C′.
图(3)
图(4)
解:
探索新知
总 结
作中心对称的图形的一般步骤是:①确定代表性的点(线段的端点);②作出每个代表性的点的对称点;③按照原图形的形状顺次连接各对称点.
学以致用
小试牛刀
1.把一个图形绕着某一点旋转________,如果它能够与另一个图形重
合,那么就说这两个图形关于这个点对称或_________,这个点叫
做它们的__________.这两个图形在旋转后能重合的对应点叫做关
于对称中心的________.
180°
中心对称
对称中心
对称点
2.成中心对称的两个图形中,对应点所连线段经过__________,且被
对称中心________,且这两个图形是全等的.
对称中心
平分
小试牛刀
3.作点A关于点O的对称点时,连接AO并延长________,即可得到点A
的对称点;作某个图形关于点O的对称图形时,先作出图形的
____________关于点O的对称点,然后顺次连接各对称点即可.
一倍
每个关键点
4.如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A
的对称点是点A′,AB⊥a于点B,A′D⊥b于点D,若OB=3,OD=
2,则阴影部分的面积之和为________.
6
小试牛刀
5.如图,△ABC与△A1B1C1关于点O成中心对称,下列结论:①∠BAC
=∠B1A1C1;②AC=A1C1;③OA=OA1;④△ABC与△A1B1C1的面
积相等.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
小试牛刀
6.把一张正方形纸片如图①、图②对折两次后,再按图③挖去一个三
角形小孔,则展开后的图形是( )
C
7.下列各组图形中,△A′B′C′与△ABC成中心对称的是( )
A
小试牛刀
8.下列说法正确的是( )
A.全等的两个图形成中心对称
B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等
D.旋转后能够重合的两个图形成中心对称
C
小试牛刀
9.如图,已知点M是△ABC的边BC的中点,点O是△ABC外一点.
(1)画△A′B′C′,使△A′B′C′与△ABC
关于点M成中心对称;
解:如图.①连接AM并延长至A′,使MA′=AM;
②点B关于点M的对称点B′即为点C,点C关于
点M的对称点C′即为点B;
③连接A′B′,A′C′,则△A′B′C′即为所求.
小试牛刀
9.如图,已知点M是△ABC的边BC的中点,点O是△ABC外一点.
(2)画△A″B″C″,使△A″B″C″与
△ABC关于点O成中心对称.
解:①连接AO,BO,CO,并分别延长至A″,B″,C″,
使OA″=AO,OB″=BO,OC″=CO;
②连接A″B″,A″C″,B″C″,则△A″B″C″即为所求.
小试牛刀
10.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成
中心对称的三角形;
解:如图,延长AD至E,使DE=AD,
连接CE,则△ECD即为所求.
小试牛刀
(2)若AB=10,AC=12,求AD长的取值范围.
解:由(1)可知AD=DE,
EC=AB=10.
在△ACE中,由AC-EC12-10即2∴2<2AD<22.∴1小试牛刀
11.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知
A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
解:根据中心对称的性质,可得对称中心的
坐标是D1D的中点,
∵点D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
小试牛刀
12.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,
D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(2)写出点B,C,B1,C1的坐标.
解:∵点A,D的坐标分别是(0,4),(0,2),∴正方形ABCD与正方形
A1B1C1D1的边长都是4-2=2.
∴点B,C的坐标分别是(-2,4),(-2,2).
∵A1D1=2,点D1的坐标是(0,3),
∴点A1的坐标是(0,1).∴点B1,C1的坐标分别是(2,1),(2,3).
课堂小结
课堂小结
中心对称
中心对称的作图
中心对称及其相关概念
中心对称性质
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
23.2.1 中心对称
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前面我们研究了旋转及其性质,现在研究一类特殊的旋转——中心对称及其性质.
新课精讲
探索新知
1
知识点
中心对称的定义
(1)如图,把其中一个图案绕点O 旋转180°,你有什么发现?
两个图案能够完全重合在一起.
问 题(一)
探索新知
(2)如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把
△OCD 绕点 O 旋转 180°,你有什么发现?
两个图案能够完全重合在一起.
A
B
D
C
O
探索新知
你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
问 题(二)
点 O
180°
重合
探索新知
探索新知
例1 如图所示的图形中成中心对称的有________组.
导引:利用中心对称的定义解答.
3
探索新知
总 结
根据中心对称的定义,看左边的图形能否绕一点旋转180°后与右边的图形重合,能就成中心对称,否则就不成,本例中第四组不成.
典题精讲
如图所示的5组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组
B.2组
C.3组
D.4组
B
探索新知
2
知识点
中心对称的性质
探 究
如图,旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A′B′C′;
第三步,移开三角板.
这样画出的△ABC 与△A′B′C′关于点O对称,分别连接对称点AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
C
A
B
C
A
B
A′
B′
O
C′
探索新知
我们可以发现:
(1)点O是线段AA′的中点.
(2)△ABC≌ △A′B′C′.
C
A
B
C′
A′
B′
O
探索新知
你能说明△ABC≌ △A′B′C′吗?
点A′是点A绕点O旋转180°得到的,
所以点O在线段AA′上,且OA=OA′,
同样地,点O也是线段BB′和CC′的中点.
在△AOB与△A′OB′中, OA=OA′,OB=OB′,AOB=∠A′OB′,
∴△AOB ≌ △ A′OB′. ∴AB=A′B′.
同理 BC=B′C′,AC=A′C′. ∴ △ABC ≌ △ A′B′C′.
C
A
B
C′
A′
B′
O
探索新知
探索新知
例2 如图,△A′B′C′与△ABC关于点O成中心对称,
你能从图中找出哪些相等的线段、相等的角、
全等的三角形以及有特殊位置关系的线段?
导引:根据中心对称的性质可知:如果两个图形关于某点成中心对
称,那么对称点所连线段都经过对称中心而且被对称中心平
分,而且这两个图形是全等图形,对应边平行(或共线)且相等.
解:可以找到:OA=OA′,OB=OB′,OC=OC′,△ABC≌ △A′B′C′,
AB A′B′,AC A′C′,BC B′C′,∠BAC=∠B′A′C′,
∠ABC=∠A′B′C′,∠ACB= ∠A′C′B′等.
探索新知
总 结
看准△ABC与△A′B′C′关于点O成中心对称的有关对称点,根据对称点来找对应线段、对应角,再由对称中心的性质得到对应线段的关系和对应角相等.
典题精讲
如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′. ED是△ABC
的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2
B.3
C.4
D.1.5
A
探索新知
3
知识点
中心对称的作图
我们已经掌握了中心对称定义和中心对称的性质. 下面我们要用所学的知识进行中心对称的作图.
探索新知
根据中心对称的性质作已知图形关于某点中心对称的图形的关键是作出某些特殊点的对称点.
作图步骤:
(1)连接原图形上的特殊点和对称中心;
(2)再将以上各线段延长找对称点,使得特殊点与对 称中心的距离和其对称点与对称中心的距离相等;
(3)将对称点按原图形的形状连接起来,即可得出原图形关于某点中心对称的图形.
探索新知
例3 (1)如图(1),选择点O为对称中心,画出点A关于点O的对
称点A′;
(2)如图(2),选择点O为对称中心,画出与△ABC关于点O
对称的△A′B′C′.
图(1)
图(2)
探索新知
(1)如图(3),连接AO,在AO的延长线上截取OA′=OA,即
可以求得点A关于点O的对称点A′.
(2)如图(4),作出A,B,C三点关于点O的对称点A′,B′,
C′,依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于点
O对称的△A′B′C′.
图(3)
图(4)
解:
探索新知
总 结
作中心对称的图形的一般步骤是:①确定代表性的点(线段的端点);②作出每个代表性的点的对称点;③按照原图形的形状顺次连接各对称点.
学以致用
小试牛刀
1.把一个图形绕着某一点旋转________,如果它能够与另一个图形重
合,那么就说这两个图形关于这个点对称或_________,这个点叫
做它们的__________.这两个图形在旋转后能重合的对应点叫做关
于对称中心的________.
180°
中心对称
对称中心
对称点
2.成中心对称的两个图形中,对应点所连线段经过__________,且被
对称中心________,且这两个图形是全等的.
对称中心
平分
小试牛刀
3.作点A关于点O的对称点时,连接AO并延长________,即可得到点A
的对称点;作某个图形关于点O的对称图形时,先作出图形的
____________关于点O的对称点,然后顺次连接各对称点即可.
一倍
每个关键点
4.如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A
的对称点是点A′,AB⊥a于点B,A′D⊥b于点D,若OB=3,OD=
2,则阴影部分的面积之和为________.
6
小试牛刀
5.如图,△ABC与△A1B1C1关于点O成中心对称,下列结论:①∠BAC
=∠B1A1C1;②AC=A1C1;③OA=OA1;④△ABC与△A1B1C1的面
积相等.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
小试牛刀
6.把一张正方形纸片如图①、图②对折两次后,再按图③挖去一个三
角形小孔,则展开后的图形是( )
C
7.下列各组图形中,△A′B′C′与△ABC成中心对称的是( )
A
小试牛刀
8.下列说法正确的是( )
A.全等的两个图形成中心对称
B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等
D.旋转后能够重合的两个图形成中心对称
C
小试牛刀
9.如图,已知点M是△ABC的边BC的中点,点O是△ABC外一点.
(1)画△A′B′C′,使△A′B′C′与△ABC
关于点M成中心对称;
解:如图.①连接AM并延长至A′,使MA′=AM;
②点B关于点M的对称点B′即为点C,点C关于
点M的对称点C′即为点B;
③连接A′B′,A′C′,则△A′B′C′即为所求.
小试牛刀
9.如图,已知点M是△ABC的边BC的中点,点O是△ABC外一点.
(2)画△A″B″C″,使△A″B″C″与
△ABC关于点O成中心对称.
解:①连接AO,BO,CO,并分别延长至A″,B″,C″,
使OA″=AO,OB″=BO,OC″=CO;
②连接A″B″,A″C″,B″C″,则△A″B″C″即为所求.
小试牛刀
10.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成
中心对称的三角形;
解:如图,延长AD至E,使DE=AD,
连接CE,则△ECD即为所求.
小试牛刀
(2)若AB=10,AC=12,求AD长的取值范围.
解:由(1)可知AD=DE,
EC=AB=10.
在△ACE中,由AC-EC
11.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知
A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
解:根据中心对称的性质,可得对称中心的
坐标是D1D的中点,
∵点D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
小试牛刀
12.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,
D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(2)写出点B,C,B1,C1的坐标.
解:∵点A,D的坐标分别是(0,4),(0,2),∴正方形ABCD与正方形
A1B1C1D1的边长都是4-2=2.
∴点B,C的坐标分别是(-2,4),(-2,2).
∵A1D1=2,点D1的坐标是(0,3),
∴点A1的坐标是(0,1).∴点B1,C1的坐标分别是(2,1),(2,3).
课堂小结
课堂小结
中心对称
中心对称的作图
中心对称及其相关概念
中心对称性质
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
