人教版(新)九上-24.1.1 圆【优质课件】
文档属性
| 名称 | 人教版(新)九上-24.1.1 圆【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共37张PPT)
24.1.1 圆
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆的定义
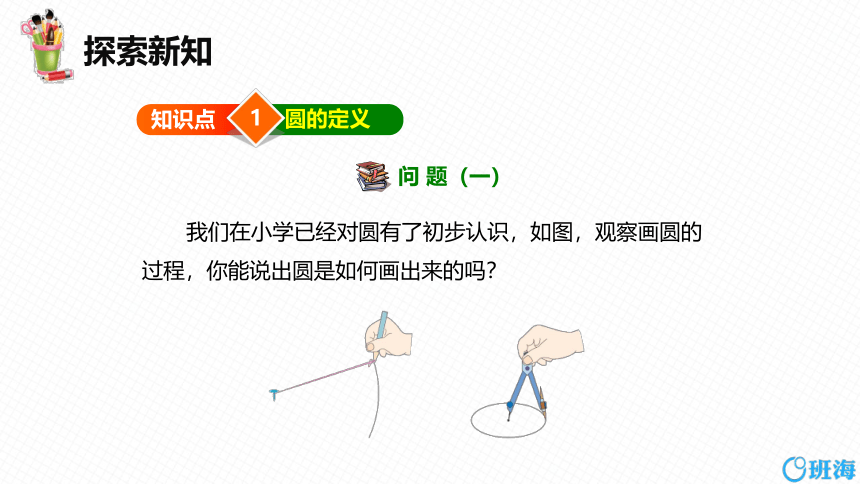
问 题(一)
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
探索新知
归 纳
在一个平面内,线段 OA 绕它固定的一个端点O 旋转一周,另一个端点 A 所形成的图形叫做圆.其固定的端点 O 叫做圆心线段 OA 叫做半径. 以点 O为圆心的圆,记作⊙O,读作“圆O”.
探索新知
问 题(二)
思考:从画圆的过程可以看出什么呢?
解答:(1)圆上各点到定点(圆心O)的距离都等于定长(半 径r);
(2)到定点的距离等于定长的点都在同一个圆上.
动态:在一个平面内,线段OA绕它固定的一个端点O旋转一周, 另一
个端 点A所形成的图形叫做圆.
静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长
r 的点组成的图形.
探索新知
归 纳
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点的集合.
确定一个圆的两个要素:圆心、半径. 圆心确定圆的位置,半径确定圆的大小.
探索新知
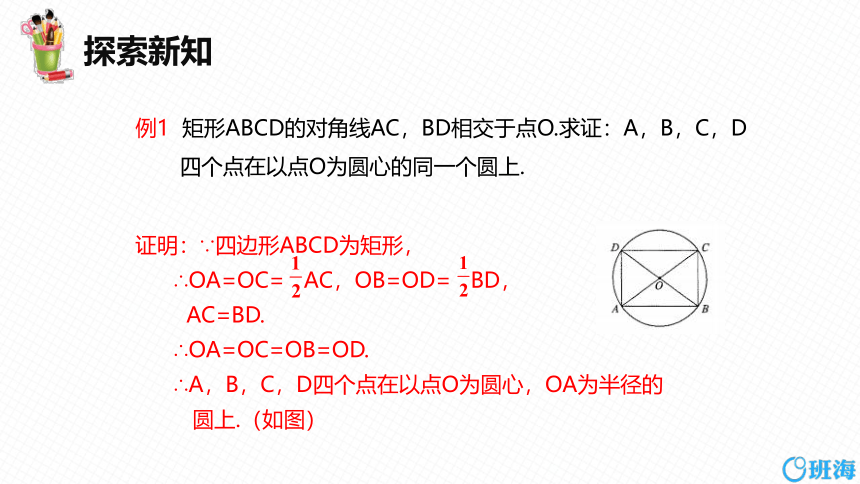
例1 矩形ABCD的对角线AC,BD相交于点O.求证:A,B,C,D
四个点在以点O为圆心的同一个圆上.
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,
AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的
圆上.(如图)
探索新知
总 结
本例运用数形结合思想,根据“数量”关系得到“位置”关系;解此例的关键是运用圆的特性,将求证几个点在同一个圆上转化为证明这几个点到某点(圆心)的距离相等.“到定点的距离相等的点在同一圆上”是今后证明多点共圆问题的一种常用方法.
典题精讲
1.如何在操场上画一个半径是5 m的圆?说出你的由.
2.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
答案不唯一
D
探索新知
2
知识点
与圆有关的概念
弦: 连接圆上任意两点的线段(如图中的AC)叫做弦经过圆心的弦(如图中的AB)叫做直径.
注意:
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是
圆中最长的弦,但弦不一定是直径.
C
A
·
O
B
探索新知
弧:圆上任意两点间的部分叫做圆弧,简称弧.如图,以A、B
为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧
都叫做半圆.
⌒
·
C
O
A
B
探索新知
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
探索新知
等圆与等弧:
能够重合的两个圆叫做等圆.容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等. 在同圆或等圆中,能够互相重合的弧叫做等弧.
探索新知
以下命题:
(1)半圆是弧,但弧不一定是半圆;
(2)过圆上任意一点只能作一条弦,且这条弦是直径;
(3)弦是直径; (4)直径是圆中最长的弦;
(5)直径不是弦; (6)优弧大于劣弧;
(7)以O为圆心可以画无数个圆.
正确的个数为( )
A.1 B.2 C.3 D.4
C
例2
探索新知
解析:(1)半圆是弧的一种,弧可以分为劣弧、半圆、弧三种,故正确;(2)过圆上任意一点可以作无数条弦,故错误;(3)直径是过圆心的特殊弦,但弦不一定是直径,故错误;(4)圆有无数条弦,过圆心的弦最长,即直径是圆中最长的弦,故正确; (5)直径是圆中最长的弦,故错误;(6)在同圆或圆中,优弧大于劣弧,故错误;(7)以一个点为圆心,若不指明半径,可画出无数个大小不等的同心圆,故正确.
探索新知
直径是过圆心的弦,因此直径是弦,但弦不一定是直径;在提到“弦”时,如果没有特别说明,不要忘记直径这种特殊的弦.
弦是圆上两点间的线段,有无数条;弧是 圆上两点间的部分,弧是曲线,弧也有无数条.
每条弧对一条弦;而每条弦所对的弧有两条:优弧、劣弧或两个半圆.
弦与直径间的关系:
弦与弧之间的关系:
典题精讲
1.下列说法中,正确的是( )
①弦是直径; ②半圆是弧; ③过圆心的线段是直径;
④半圆是最长的弧; ⑤直径是圆中最长的弦.
A.②③ B.③⑤
C.④⑤ D.②⑤
D
典题精讲
2.如图,点A,B,C在⊙O上,点O在线段AC上,点D在线段AB上,
下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
探索新知
3
知识点
同圆的半径相等
圆的性质:
同圆的半径相等.从等圆的定义容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等.
探索新知
例3 如图,在⊙O中,OA,OB是半径,C,D为OA,OB上的两
点,且AC=BD,求证:AD=BC.
导引:要证AD=BC,需证其所在的三角形全等,即需证△ADO≌△BCO.
探索新知
证明:∵OA,OB是半径,∴OA=OB.
又∵AC=BD,∴OC=OD.
在△ADO和△BCO中,
∴△ADO≌△BCO.
∴AD=BC.
探索新知
总 结
(1)本例中的OA=OB,即“圆的半径相等”,在以后的证
明中,可直接应用.
(2)“同圆的半径相等”在证明圆中线段相等时有着广泛应
用,应熟练掌握.
典题精讲
1.如图,点A,D,G,M在半圆O上,四边形ABOC,四边形OFDE,
四边形HMNO都是矩形,设BC=a,EF=b, NH=c,则下列各
式正确的是( )
A.a>b>c
B.a=b=c
C.c>a>b
D.b>c>a
B
典题精讲
2.如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径
作圆,交x轴的正半轴于点C,则∠BAC等于________度.
60°
学以致用
小试牛刀
1.圆的形成定义:在一个平面内,线段绕它固定的一个端点旋转
________,另一个端点所形成的图形叫做圆.
2.圆的集合定义:圆心为O、半径为r的圆可以看成是所有到定点O
的距离等于________的点的集合.
3.如图24—1—3所示,在⊙O中,_____是直径,___________是弦,
劣弧有____________,优弧有_________________.
一周
定长r
AD
AD,AC
AC,CD
ADC,CAD
小试牛刀
5.如图,在⊙O中,点A,O,D以及点B,O,C分别在一条直线
上,图中弦的条数是( )
A.2
B.3
C.5
D.6
B
4.若圆的半径为3,则弦AB的长度的取值范围是______________.
0<AB≤6
小试牛刀
6.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;
②圆的任意一条弦把圆分成优弧和劣弧两部分;
③长度相等的弧是等弧;
④半径相等的圆是等圆;
⑤直径是圆中最长的弦.
A.2个 B.3个 C.4个 D.5个
A
小试牛刀
7.如图所示,以坐标原点O为圆心的圆与y轴交于点A,B,且OA=1,
则点B的坐标是( )
A.(0,1) B. (0,-1)
C.(1,0) D. (-1,0)
A
8.如图,AB是⊙O的直径,点D,C在⊙O上,AD//OC,∠DAB=60°,
连接AC,则∠DAC等于( )
A.15° B. 30°
C. 45° D. 60°
B
小试牛刀
9.如图24—1—11所示,AB是⊙O的弦,半径OC,
OD分别交AB于点E,F,且AE=BF,请你指出
线段OE与OF的数量关系,并给予证明.
解:OE=OF.
证明:连接OA,OB.
∵OA=OB, ∴∠A=∠B.
又∵AE=BF, ∴△OAE≌△OBF, ∴OE=OF.
小试牛刀
10.已知:如图24—1—2,OA,OB为⊙O的半径,C,D分别为OA,
OB的中点.求证:AD=BC.
证明:∵OA,OB为⊙O的半径,
∴OA=OB.
∵C,D分别为OA,OB的中点, ∴OC=OD.
在△AOD和△BOC中,∵OA=OB,∠O=∠O,OD=OC,
∴△AOD≌△BOC(SAS),∴AD=BC.
课堂小结
课堂小结
半径
弦和弧
圆心
圆的定义
圆的相关概念
构建
理解圆的定义要注意两层含义:
(1)圆上各点到圆心的距离都相等.在圆所在的平面内,到圆心距离等于半径的点必定在圆上;
(2)当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的运动轨迹就是一个圆.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
24.1.1 圆
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆的定义
问 题(一)
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
探索新知
归 纳
在一个平面内,线段 OA 绕它固定的一个端点O 旋转一周,另一个端点 A 所形成的图形叫做圆.其固定的端点 O 叫做圆心线段 OA 叫做半径. 以点 O为圆心的圆,记作⊙O,读作“圆O”.
探索新知
问 题(二)
思考:从画圆的过程可以看出什么呢?
解答:(1)圆上各点到定点(圆心O)的距离都等于定长(半 径r);
(2)到定点的距离等于定长的点都在同一个圆上.
动态:在一个平面内,线段OA绕它固定的一个端点O旋转一周, 另一
个端 点A所形成的图形叫做圆.
静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长
r 的点组成的图形.
探索新知
归 纳
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点的集合.
确定一个圆的两个要素:圆心、半径. 圆心确定圆的位置,半径确定圆的大小.
探索新知
例1 矩形ABCD的对角线AC,BD相交于点O.求证:A,B,C,D
四个点在以点O为圆心的同一个圆上.
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,
AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的
圆上.(如图)
探索新知
总 结
本例运用数形结合思想,根据“数量”关系得到“位置”关系;解此例的关键是运用圆的特性,将求证几个点在同一个圆上转化为证明这几个点到某点(圆心)的距离相等.“到定点的距离相等的点在同一圆上”是今后证明多点共圆问题的一种常用方法.
典题精讲
1.如何在操场上画一个半径是5 m的圆?说出你的由.
2.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
答案不唯一
D
探索新知
2
知识点
与圆有关的概念
弦: 连接圆上任意两点的线段(如图中的AC)叫做弦经过圆心的弦(如图中的AB)叫做直径.
注意:
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是
圆中最长的弦,但弦不一定是直径.
C
A
·
O
B
探索新知
弧:圆上任意两点间的部分叫做圆弧,简称弧.如图,以A、B
为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧
都叫做半圆.
⌒
·
C
O
A
B
探索新知
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
探索新知
等圆与等弧:
能够重合的两个圆叫做等圆.容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等. 在同圆或等圆中,能够互相重合的弧叫做等弧.
探索新知
以下命题:
(1)半圆是弧,但弧不一定是半圆;
(2)过圆上任意一点只能作一条弦,且这条弦是直径;
(3)弦是直径; (4)直径是圆中最长的弦;
(5)直径不是弦; (6)优弧大于劣弧;
(7)以O为圆心可以画无数个圆.
正确的个数为( )
A.1 B.2 C.3 D.4
C
例2
探索新知
解析:(1)半圆是弧的一种,弧可以分为劣弧、半圆、弧三种,故正确;(2)过圆上任意一点可以作无数条弦,故错误;(3)直径是过圆心的特殊弦,但弦不一定是直径,故错误;(4)圆有无数条弦,过圆心的弦最长,即直径是圆中最长的弦,故正确; (5)直径是圆中最长的弦,故错误;(6)在同圆或圆中,优弧大于劣弧,故错误;(7)以一个点为圆心,若不指明半径,可画出无数个大小不等的同心圆,故正确.
探索新知
直径是过圆心的弦,因此直径是弦,但弦不一定是直径;在提到“弦”时,如果没有特别说明,不要忘记直径这种特殊的弦.
弦是圆上两点间的线段,有无数条;弧是 圆上两点间的部分,弧是曲线,弧也有无数条.
每条弧对一条弦;而每条弦所对的弧有两条:优弧、劣弧或两个半圆.
弦与直径间的关系:
弦与弧之间的关系:
典题精讲
1.下列说法中,正确的是( )
①弦是直径; ②半圆是弧; ③过圆心的线段是直径;
④半圆是最长的弧; ⑤直径是圆中最长的弦.
A.②③ B.③⑤
C.④⑤ D.②⑤
D
典题精讲
2.如图,点A,B,C在⊙O上,点O在线段AC上,点D在线段AB上,
下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
探索新知
3
知识点
同圆的半径相等
圆的性质:
同圆的半径相等.从等圆的定义容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等.
探索新知
例3 如图,在⊙O中,OA,OB是半径,C,D为OA,OB上的两
点,且AC=BD,求证:AD=BC.
导引:要证AD=BC,需证其所在的三角形全等,即需证△ADO≌△BCO.
探索新知
证明:∵OA,OB是半径,∴OA=OB.
又∵AC=BD,∴OC=OD.
在△ADO和△BCO中,
∴△ADO≌△BCO.
∴AD=BC.
探索新知
总 结
(1)本例中的OA=OB,即“圆的半径相等”,在以后的证
明中,可直接应用.
(2)“同圆的半径相等”在证明圆中线段相等时有着广泛应
用,应熟练掌握.
典题精讲
1.如图,点A,D,G,M在半圆O上,四边形ABOC,四边形OFDE,
四边形HMNO都是矩形,设BC=a,EF=b, NH=c,则下列各
式正确的是( )
A.a>b>c
B.a=b=c
C.c>a>b
D.b>c>a
B
典题精讲
2.如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径
作圆,交x轴的正半轴于点C,则∠BAC等于________度.
60°
学以致用
小试牛刀
1.圆的形成定义:在一个平面内,线段绕它固定的一个端点旋转
________,另一个端点所形成的图形叫做圆.
2.圆的集合定义:圆心为O、半径为r的圆可以看成是所有到定点O
的距离等于________的点的集合.
3.如图24—1—3所示,在⊙O中,_____是直径,___________是弦,
劣弧有____________,优弧有_________________.
一周
定长r
AD
AD,AC
AC,CD
ADC,CAD
小试牛刀
5.如图,在⊙O中,点A,O,D以及点B,O,C分别在一条直线
上,图中弦的条数是( )
A.2
B.3
C.5
D.6
B
4.若圆的半径为3,则弦AB的长度的取值范围是______________.
0<AB≤6
小试牛刀
6.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;
②圆的任意一条弦把圆分成优弧和劣弧两部分;
③长度相等的弧是等弧;
④半径相等的圆是等圆;
⑤直径是圆中最长的弦.
A.2个 B.3个 C.4个 D.5个
A
小试牛刀
7.如图所示,以坐标原点O为圆心的圆与y轴交于点A,B,且OA=1,
则点B的坐标是( )
A.(0,1) B. (0,-1)
C.(1,0) D. (-1,0)
A
8.如图,AB是⊙O的直径,点D,C在⊙O上,AD//OC,∠DAB=60°,
连接AC,则∠DAC等于( )
A.15° B. 30°
C. 45° D. 60°
B
小试牛刀
9.如图24—1—11所示,AB是⊙O的弦,半径OC,
OD分别交AB于点E,F,且AE=BF,请你指出
线段OE与OF的数量关系,并给予证明.
解:OE=OF.
证明:连接OA,OB.
∵OA=OB, ∴∠A=∠B.
又∵AE=BF, ∴△OAE≌△OBF, ∴OE=OF.
小试牛刀
10.已知:如图24—1—2,OA,OB为⊙O的半径,C,D分别为OA,
OB的中点.求证:AD=BC.
证明:∵OA,OB为⊙O的半径,
∴OA=OB.
∵C,D分别为OA,OB的中点, ∴OC=OD.
在△AOD和△BOC中,∵OA=OB,∠O=∠O,OD=OC,
∴△AOD≌△BOC(SAS),∴AD=BC.
课堂小结
课堂小结
半径
弦和弧
圆心
圆的定义
圆的相关概念
构建
理解圆的定义要注意两层含义:
(1)圆上各点到圆心的距离都相等.在圆所在的平面内,到圆心距离等于半径的点必定在圆上;
(2)当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的运动轨迹就是一个圆.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
