人教版(新)九上-24.1.2 垂直于弦的直径【优质课件】
文档属性
| 名称 | 人教版(新)九上-24.1.2 垂直于弦的直径【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览










文档简介
(共32张PPT)
24.1.2
垂直于弦的直径
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
导入新知
如图,1 400 多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(精确到 0.1 m).
新课精讲
探索新知
1
知识点
圆的对称性
问 题(一)
剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了什么?
探索新知
问 题(二)
不借助任何工具,你能找到圆形纸片的圆心吗?由此你得到了什么结论?你能证明你的结论吗?
探索新知
归 纳
通过探究可以发现,圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
探索新知
例1 求证:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
导引:要证明圆是轴对称图形,只需证明圆上任意一点 关于直径所在直线(对称轴)的对称点也在圆上.
证明:如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.过点A作AA′⊥CD,交⊙O于点A′,垂足为M,连接OA,OA′.
在△OAA′中,∵OA=OA′,
∴△OAA′是等腰三角形.又AA′⊥CD,
∴AM=MA′.即CD是AA′的垂直平分线.
这就是说,对于圆上任意一点A,在圆
上都有关于直线CD的对称点A′,因此⊙O关于直线CD对称.即圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
典题精讲
1.下列说法中不正确的是( )
A.经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.圆的对称轴有无数条
D.当圆绕它的圆心旋转60°时,仍会与原来的圆重合
A
典题精讲
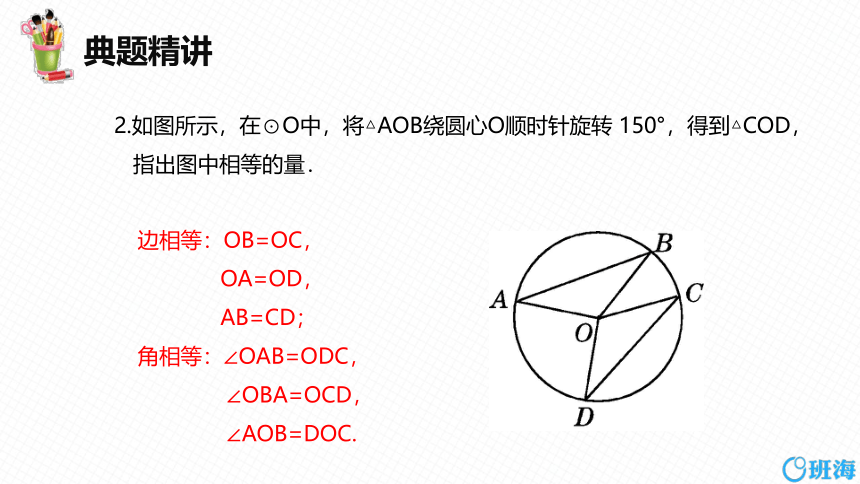
2.如图所示,在⊙O中,将△AOB绕圆心O顺时针旋转 150°,得到△COD,
指出图中相等的量.
边相等:OB=OC,
OA=OD,
AB=CD;
角相等:∠OAB=ODC,
∠OBA=OCD,
∠AOB=DOC.
探索新知
2
知识点
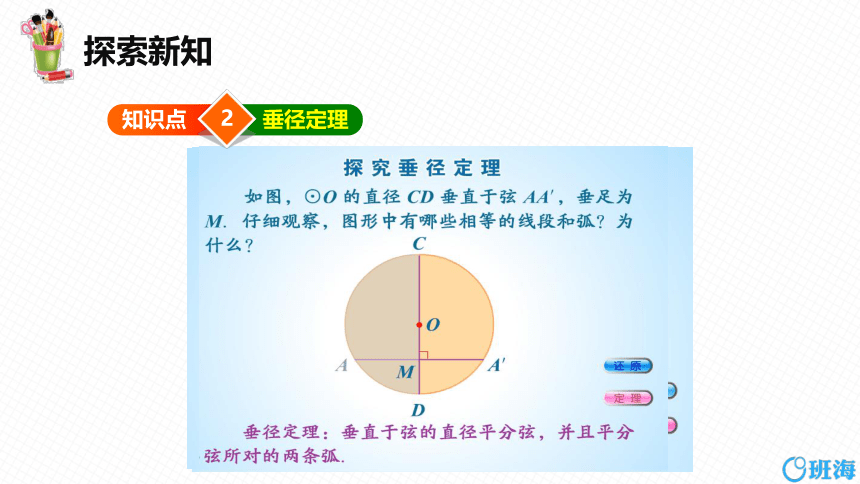
垂径定理
探索新知
下列哪些图形可以用垂径定理?你能说明理由吗?
D
O
C
A
E
B
D
O
C
A
E
B
图1
图2
图3
图4
O
A
E
B
D
O
C
A
E
B
探索新知
例2 赵州桥(如图)是我国隋代建造的石拱桥,距今约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
分析:解决此问题的关键是根据赵州桥的实物图画出几何图形.
探索新知
解:
如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,D为垂足,OC与AB相交于点C,
连接OA,根据垂径定理,D是AB的中点,C是AB的中点,CD
就是拱高.由题设可知AB=37,CD=7.23,
所以 AD= AB= 37=18.5,OD=OC-CD=R-7.23.
在Rt△OAD中,由勾股定理,
得OA2=AD2+OD2,
即R2=18.52+(R-7.23)2.
解得R≈27.3.
因此,赵州桥的主桥拱半径约为27.3 m.
⌒
⌒
⌒
⌒
探索新知
总 结
(1)“垂直于弦的直径”中的“直径”,还可以是垂直于弦的半径或过圆心垂直于弦的直线;其实质是:过圆心且垂直于弦的线段、直线均可.
(2)垂径定理中的弦可以为直径.
(3)垂径定理是证线段、弧相等的重要依据.
典题精讲
1.如图,在⊙O中,弦AB的长为8 cm,圆心O到AB的距离为3 cm.
求⊙O的半径.
由图可知,AE=BE= AB
∵OE=3cm,AB=8cm,
∴BC=4cm
在Rt△OEA中,OA= 4 +3 =5cm
即⊙O的半径是5cm.
1
2
典题精讲
2.如图,已知⊙O的直径AB⊥CD于点E,则下列结论中错误的是( )
A.CE=DE
B.AE=OE
C. BC=BD
D.△OCE≌△ODE
⌒
⌒
B
探索新知
3
知识点
垂径定理的推论
通过垂径定理的证明及应用,我们还可以进一步得到垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
探索新知
例3 如图所示,⊙O的直径CD=10 cm,AB是⊙O的弦, AM= BM,OM∶OC=3∶5,求AB的长.
解:∵圆O的直径CD=10cm,
∴圆O的半径为5cm,即OC=5cm,
∵OM:OC=3:5,
∴OM= OC=3cm,
连接OA,∵AB⊥CD,
∴M为AB的中点,即AM=BM= AB,
在Rt△AOM中,OA=5cm,OM=3cm,
根据勾股定理得:AM=
则AB=2AM=8cm.
探索新知
关于垂径定理及其推论可归纳为:
一条直线,它具备以下五个性质:
直线过圆心;
(2)直线垂直于弦;
(3)直线平分弦(不是直径);
(4) 直线平分弦所对的优弧;
(5)直线平分弦所对的劣弧.
如果把其中的任意两条作为条件,其余三条作为结论,组成的命题都是真命题.
典题精讲
图,AB是⊙O的直径,∠BAC=42°,点D是弦AC 的中点,则∠DOC的度数是________度.
48°
学以致用
小试牛刀
D
1.如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中
不一正确的是( )
A.∠COE=∠DOE
B.CE=DE
C.
D.OE=BE
小试牛刀
2.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为点N,
则ON=( )
A.5 B.7
C.9 D.11
3.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=12,BE=2,
则⊙O的直径为( )
A.8 B.10
C.16 D.20
A
D
小试牛刀
4.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,
B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于
点F,则EF=( )
A.4
B.5
C.5.5
D.6
B
小试牛刀
5.如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴
交于点B,C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,
OC=6,则⊙O′的半径为( )
A.7
B.6
C.5
D.4
C
小试牛刀
6.如图,已知⊙O的半径为5,弦AB=8,P是弦
AB上一点,且PB=2, 求 OP的长.
小试牛刀
课堂小结
课堂小结
通过本课时的学习,需要我们:
1.理解圆的轴对称性及垂径定理的推证过程;能初步应用垂径定理进行计算和证明;
2.掌握垂径定理的推论,明确理解“知二得三”的意义.利用垂径定理及其推论解决相应的数学问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
24.1.2
垂直于弦的直径
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
导入新知
如图,1 400 多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(精确到 0.1 m).
新课精讲
探索新知
1
知识点
圆的对称性
问 题(一)
剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了什么?
探索新知
问 题(二)
不借助任何工具,你能找到圆形纸片的圆心吗?由此你得到了什么结论?你能证明你的结论吗?
探索新知
归 纳
通过探究可以发现,圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
探索新知
例1 求证:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
导引:要证明圆是轴对称图形,只需证明圆上任意一点 关于直径所在直线(对称轴)的对称点也在圆上.
证明:如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.过点A作AA′⊥CD,交⊙O于点A′,垂足为M,连接OA,OA′.
在△OAA′中,∵OA=OA′,
∴△OAA′是等腰三角形.又AA′⊥CD,
∴AM=MA′.即CD是AA′的垂直平分线.
这就是说,对于圆上任意一点A,在圆
上都有关于直线CD的对称点A′,因此⊙O关于直线CD对称.即圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
典题精讲
1.下列说法中不正确的是( )
A.经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.圆的对称轴有无数条
D.当圆绕它的圆心旋转60°时,仍会与原来的圆重合
A
典题精讲
2.如图所示,在⊙O中,将△AOB绕圆心O顺时针旋转 150°,得到△COD,
指出图中相等的量.
边相等:OB=OC,
OA=OD,
AB=CD;
角相等:∠OAB=ODC,
∠OBA=OCD,
∠AOB=DOC.
探索新知
2
知识点
垂径定理
探索新知
下列哪些图形可以用垂径定理?你能说明理由吗?
D
O
C
A
E
B
D
O
C
A
E
B
图1
图2
图3
图4
O
A
E
B
D
O
C
A
E
B
探索新知
例2 赵州桥(如图)是我国隋代建造的石拱桥,距今约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
分析:解决此问题的关键是根据赵州桥的实物图画出几何图形.
探索新知
解:
如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,D为垂足,OC与AB相交于点C,
连接OA,根据垂径定理,D是AB的中点,C是AB的中点,CD
就是拱高.由题设可知AB=37,CD=7.23,
所以 AD= AB= 37=18.5,OD=OC-CD=R-7.23.
在Rt△OAD中,由勾股定理,
得OA2=AD2+OD2,
即R2=18.52+(R-7.23)2.
解得R≈27.3.
因此,赵州桥的主桥拱半径约为27.3 m.
⌒
⌒
⌒
⌒
探索新知
总 结
(1)“垂直于弦的直径”中的“直径”,还可以是垂直于弦的半径或过圆心垂直于弦的直线;其实质是:过圆心且垂直于弦的线段、直线均可.
(2)垂径定理中的弦可以为直径.
(3)垂径定理是证线段、弧相等的重要依据.
典题精讲
1.如图,在⊙O中,弦AB的长为8 cm,圆心O到AB的距离为3 cm.
求⊙O的半径.
由图可知,AE=BE= AB
∵OE=3cm,AB=8cm,
∴BC=4cm
在Rt△OEA中,OA= 4 +3 =5cm
即⊙O的半径是5cm.
1
2
典题精讲
2.如图,已知⊙O的直径AB⊥CD于点E,则下列结论中错误的是( )
A.CE=DE
B.AE=OE
C. BC=BD
D.△OCE≌△ODE
⌒
⌒
B
探索新知
3
知识点
垂径定理的推论
通过垂径定理的证明及应用,我们还可以进一步得到垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
探索新知
例3 如图所示,⊙O的直径CD=10 cm,AB是⊙O的弦, AM= BM,OM∶OC=3∶5,求AB的长.
解:∵圆O的直径CD=10cm,
∴圆O的半径为5cm,即OC=5cm,
∵OM:OC=3:5,
∴OM= OC=3cm,
连接OA,∵AB⊥CD,
∴M为AB的中点,即AM=BM= AB,
在Rt△AOM中,OA=5cm,OM=3cm,
根据勾股定理得:AM=
则AB=2AM=8cm.
探索新知
关于垂径定理及其推论可归纳为:
一条直线,它具备以下五个性质:
直线过圆心;
(2)直线垂直于弦;
(3)直线平分弦(不是直径);
(4) 直线平分弦所对的优弧;
(5)直线平分弦所对的劣弧.
如果把其中的任意两条作为条件,其余三条作为结论,组成的命题都是真命题.
典题精讲
图,AB是⊙O的直径,∠BAC=42°,点D是弦AC 的中点,则∠DOC的度数是________度.
48°
学以致用
小试牛刀
D
1.如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中
不一正确的是( )
A.∠COE=∠DOE
B.CE=DE
C.
D.OE=BE
小试牛刀
2.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为点N,
则ON=( )
A.5 B.7
C.9 D.11
3.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=12,BE=2,
则⊙O的直径为( )
A.8 B.10
C.16 D.20
A
D
小试牛刀
4.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,
B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于
点F,则EF=( )
A.4
B.5
C.5.5
D.6
B
小试牛刀
5.如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴
交于点B,C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,
OC=6,则⊙O′的半径为( )
A.7
B.6
C.5
D.4
C
小试牛刀
6.如图,已知⊙O的半径为5,弦AB=8,P是弦
AB上一点,且PB=2, 求 OP的长.
小试牛刀
课堂小结
课堂小结
通过本课时的学习,需要我们:
1.理解圆的轴对称性及垂径定理的推证过程;能初步应用垂径定理进行计算和证明;
2.掌握垂径定理的推论,明确理解“知二得三”的意义.利用垂径定理及其推论解决相应的数学问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
