人教版(新)九上-24.2.1 点和圆的位置关系【优质课件】
文档属性
| 名称 | 人教版(新)九上-24.2.1 点和圆的位置关系【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览










文档简介
(共42张PPT)
24.2.1 点和圆
的位置关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
新课精讲
探索新知
1
知识点
点与圆的位置关系
探究:
1. 请你在练习本上画一个圆,然后任意做一些点,观察这些点和圆的位置关系.
2. 量一量这些点到圆心的距离,你发现了什么?
探索新知
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
点P在圆外 d>r;
点P在圆上 d=r;
点P在圆内 d<r.
符号“ ”读作“等价于”,
它表示从符号“ ”的左
端可以推出右端,从右
端也可以推出左端.
探索新知
例1 已知⊙O的半径r=5 cm,圆心O到直线l的距离d=OD=3 cm,在直线l上有P,Q,R三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R三点与⊙O的位置关系各是怎样的?
要判断点和圆的位置关系,实质上是要比较点到圆
心的距离与半径的大小,而半径为已知量,即需求
出相关点到圆心的距离.
导引:
探索新知
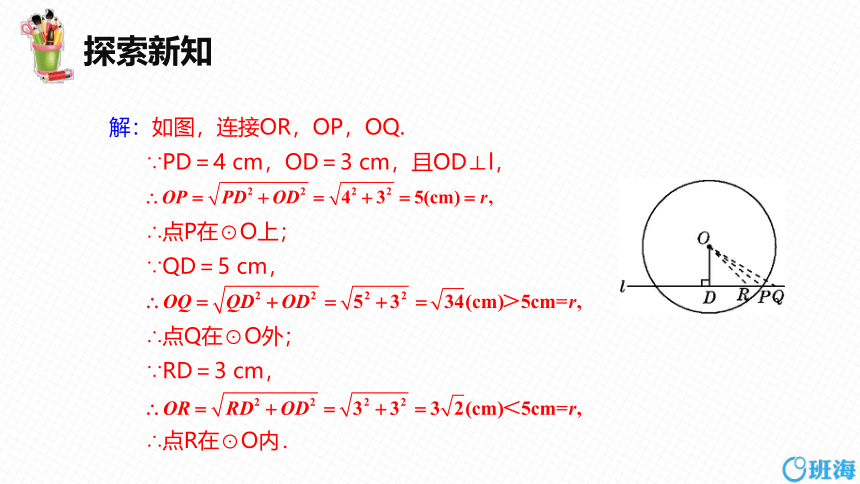
解:如图,连接OR,OP,OQ.
∵PD=4 cm,OD=3 cm,且OD⊥l,
∴点P在⊙O上;
∵QD=5 cm,
∴点Q在⊙O外;
∵RD=3 cm,
∴点R在⊙O内.
探索新知
总 结
判断点和圆的位置关系,关键是计算出点到圆心的距离,再与圆的半径比较大小,由数量关系决定位置关系;构造直角三角形并运用勾股定理是求距离的常用辅助方法.
典题精讲
1.⊙O的半径为5 cm,点A到圆心O的距离OA=4 cm,则点A与圆
O的位置关系为( )
A.点A在圆上
B.点A在圆内
C.点A在圆外
D.无法确定
B
典题精讲
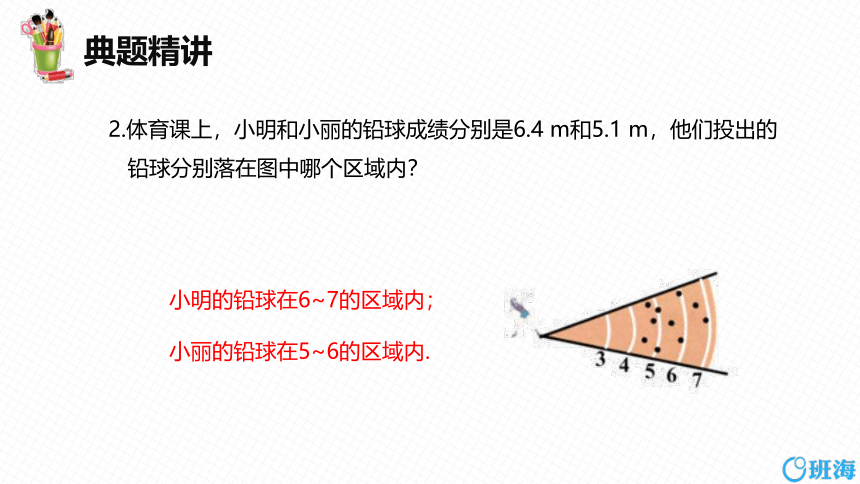
2.体育课上,小明和小丽的铅球成绩分别是6.4 m和5.1 m,他们投出的
铅球分别落在图中哪个区域内?
小明的铅球在6~7的区域内;
小丽的铅球在5~6的区域内.
探索新知
2
知识点
确定圆的条件
过一个已知点A如何作圆?
过点A所作圆的圆心在哪里?半径多大?可以作几个这样的圆?
探 究(一)
A
探索新知
过已知两点A、B如何作圆?
圆心A、B两点的距离怎样?能用式子表示吗?圆心在哪里?过点A、B两点的圆有几个?
探 究(二)
A
B
探索新知
探 究(三)
过同一平面内三个点情况会怎样呢?
1.不在同一直线上的三点A、B、C.
定理:过不在同一直线上的三点确定一个圆.
2.过在同一直线上的三点A、B、C可以作几个圆?
不能作出
O
A
B
C
D
E
F
G
探索新知
例2 如图,点A,B,C在同一条直线上,点D在直线AB外,过这4个点中
的任意3个点,能画圆的个数是( )
A.1 B.2 C.3 D.4
在4个点中取3个点确定一个圆,关键是
这3个点要不在同一直线上,因此本题
的实质是在A,B,C中找2个点与点
D确定圆.根据题意得出:点D,A,B;点D,A,C;点
D,B,C可以分别确定一个圆.故过这4个点中的任意3
个点,能画圆的个数是3.故选C.
C
导引:
探索新知
总 结
确定一个圆的条件:
(1)已知圆心、半径,可以确定一个圆.
(2)不在同一条直线上的三个点确定一个圆.
典题精讲
1.下列关于确定一个圆的说法中,正确的是( )
A.三个点一定能确定一个圆
B.以已知线段为半径能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
2.已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
C
B
探索新知
3
知识点
三角形的外接圆
试一试:
任意画一个三角形,然后再画出经过三个顶点的圆.
A
B
C
O
探索新知
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
探索新知
例3 如图,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O 的半径.
导引:要求⊙O的半径,已知弦AB的长,需以
AB为边与⊙O的半径(或直径)构成等腰直角三
角形,因此有两个切入点.
方法一:如图1,连接OA,OB,利用圆周角
定理可得∠AOB=2∠C=90°,再利用勾股定
理求出半径;方法二:如图2,作直径AD,连接BD,利用同弧所对的圆周角相等,得∠D=∠C=45°,再利用勾股定理可求出半径.
探索新知
解:方法一:如图1,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图 1
探索新知
方法二:如图2,作直径AD,连接BD,设⊙O的半径为r.
∵AD为⊙O的直径,∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°,
∴BD=AB=4.
在Rt△ABD中,AB2+BD2=AD2,
即42+42=(2r)2,
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图 2
探索新知
总 结
求三角形的外接圆半径时,最常用的办法是作出圆心与三角形顶点的连线(即半径),延长使这条半径变为直径,将求半径转化为直角三角形中求边的长.
典题精讲
如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心?
如图所示,根据垂径定理的推论,两个直径的交点即为圆心.
探索新知
4
知识点
反证法
思考:经过同一条直线上的三个点能作出一个圆吗?
如图,假设经过同一条直线l上的A,B,C三点可以作一个圆.设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,
而l1⊥l,l2⊥l,这与我们以前学过的“过一点
有且只有一条直线与已知直线垂直”矛盾. 所
以,经过同一条直线上的三个点不能作圆.
探索新知
归 纳
上面证明“经过同一条直线上的三个点不能作圆”的方法与我们以前学过的证明不同,它不是直接从命题的已知得出结论,而是假设命题的结论不成立(即假设经过同一条直线上的三个点可以作一个圆),由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.这种方法叫做反证法.
探索新知
例4 用反证法证明平行线的性质“两直线平行,同位角相等”.
如图,我们要证明:如果AB∥CD,那么∠1=∠2.
假设∠1≠∠2,过点O作直线A′B′,
使∠EOB′=∠2.根据
“同位角相等,两直线平行”,可
得A′B′∥CD.这样,过点O就有
两条直线AB,A′B′都平行于CD,这与平行公理“过
直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,从而∠1=∠2.
证明:
探索新知
总 结
(1)反证法适用情形:①命题的结论的表述为“肯定”或“否定”,且用直接法证较困难;②证明一个定理的逆命题,用直接法证较困难.使用反证法的前提条件是“结论”的反面可列举出来.
(2)反证法使用要经历:反设→归谬→结论这三步,反设是推理归纳的已知条件,即把反设作为已知条件进行推理;归谬是关键,是反证法的核心,其作用是:从命题结论的反面出发,推出与已知事理(定义、公理、定理、已知条件)矛盾;最后说明假设不成立,原结论成立.
典题精讲
1.用反证法证明命题“三角形中必有一个内角小于或等于60°” 时,首先应假设三角形中( )
A.有一个内角大于60° B.有一个内角小于60°
C.每一个内角都大于60° D.每一个内角都小于60°
2.用反证法证明命题“若⊙O的半径为r,点P到圆心的距离为d,且d>r,则点P在⊙O的外部”,应先假设______________________________.
C
点P在⊙O上或点P在⊙O内
学以致用
小试牛刀
1.过点A,B的圆有无数个,这些圆的圆心都在线段AB的_____________上,当圆心O确定之后,OA或OB即为圆的_______.
垂直平分线
半径
2.如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为____.
3.用反证法证明“三角形中至少有一个角不小于60°”第一步假设为:
_______________________________.
18°
三角形中三个角都小于60°
小试牛刀
4.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴
到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则
圆的半径为______cm.
5.已知点P在半径为5的⊙O外,如果设OP=x,那么x的取值范围是
_____.
x>5
小试牛刀
6.已知⊙O的半径为6,A为线段PO的中点,当OP=10时,点A与⊙O
的位置关系为( )
A.在圆上 B.在圆外
C.在圆内 D.不确定
7.在平面直角坐标系xOy中,⊙O的半径为4,点P的坐标为(3,4), 则
点P的位置为( )
A.在⊙O外 B.在⊙O上
C.在⊙O内 D.不确定
C
A
小试牛刀
8.根据下列条件可以确定一个圆的是( )
A.已知圆心 B.已知半径
C.已知直径 D.三个点
9.若⊙O所在平面内一点P到⊙O上的最大距离为3,最小距离为1,
则此圆的半径为( )
A.2或1 B.2或4 C.2 D.1
C
A
小试牛刀
解:(1)答案不唯一,如图所示.
10.如图,在矩形ABCD中,AB=2,AD=4.
(1)以点A为圆心画两个同心圆,使点B在小圆内,点C在大圆外;
小试牛刀
10.如图,在矩形ABCD中,AB=2,AD=4.
(2)以点A为圆心画⊙A,设⊙A的半径为R,若点B,C,D三点中至少有一点在⊙A内,且至少有一点在⊙A外,求R的取值范围.
小试牛刀
解:由SAS可证.
11.如图①,在△ABC中,BA=BC,D是平面内不与点A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
小试牛刀
解: 四边形BECD是菱形.
证明:∵△ABD≌△CBE,∴AD=CE.
∵点D是△ABC的外接圆圆心,
∴DA=DB=DC. 又∵BD=BE,
∴BD=BE=EC=CD,∴四边形BECD是菱形.
11.如图①,在△ABC中,BA=BC,D是平面内不与点A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(2)如图②,当点D是△ABC的外接圆圆心时,请判断四边形BECD的形状,并证明你的结论.
课堂小结
课堂小结
1.点和圆的三种位置关系:设⊙O的半径为r,点P到圆心
的距离为d,则
2.过一点可以作无数个圆.
3.过两点可以作无数个圆.圆心在以已知两点为端点的线
段的垂直平分线上.
4.过三点
5.反证法的证明思想:反设、归谬、结论.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
24.2.1 点和圆
的位置关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
新课精讲
探索新知
1
知识点
点与圆的位置关系
探究:
1. 请你在练习本上画一个圆,然后任意做一些点,观察这些点和圆的位置关系.
2. 量一量这些点到圆心的距离,你发现了什么?
探索新知
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
点P在圆外 d>r;
点P在圆上 d=r;
点P在圆内 d<r.
符号“ ”读作“等价于”,
它表示从符号“ ”的左
端可以推出右端,从右
端也可以推出左端.
探索新知
例1 已知⊙O的半径r=5 cm,圆心O到直线l的距离d=OD=3 cm,在直线l上有P,Q,R三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R三点与⊙O的位置关系各是怎样的?
要判断点和圆的位置关系,实质上是要比较点到圆
心的距离与半径的大小,而半径为已知量,即需求
出相关点到圆心的距离.
导引:
探索新知
解:如图,连接OR,OP,OQ.
∵PD=4 cm,OD=3 cm,且OD⊥l,
∴点P在⊙O上;
∵QD=5 cm,
∴点Q在⊙O外;
∵RD=3 cm,
∴点R在⊙O内.
探索新知
总 结
判断点和圆的位置关系,关键是计算出点到圆心的距离,再与圆的半径比较大小,由数量关系决定位置关系;构造直角三角形并运用勾股定理是求距离的常用辅助方法.
典题精讲
1.⊙O的半径为5 cm,点A到圆心O的距离OA=4 cm,则点A与圆
O的位置关系为( )
A.点A在圆上
B.点A在圆内
C.点A在圆外
D.无法确定
B
典题精讲
2.体育课上,小明和小丽的铅球成绩分别是6.4 m和5.1 m,他们投出的
铅球分别落在图中哪个区域内?
小明的铅球在6~7的区域内;
小丽的铅球在5~6的区域内.
探索新知
2
知识点
确定圆的条件
过一个已知点A如何作圆?
过点A所作圆的圆心在哪里?半径多大?可以作几个这样的圆?
探 究(一)
A
探索新知
过已知两点A、B如何作圆?
圆心A、B两点的距离怎样?能用式子表示吗?圆心在哪里?过点A、B两点的圆有几个?
探 究(二)
A
B
探索新知
探 究(三)
过同一平面内三个点情况会怎样呢?
1.不在同一直线上的三点A、B、C.
定理:过不在同一直线上的三点确定一个圆.
2.过在同一直线上的三点A、B、C可以作几个圆?
不能作出
O
A
B
C
D
E
F
G
探索新知
例2 如图,点A,B,C在同一条直线上,点D在直线AB外,过这4个点中
的任意3个点,能画圆的个数是( )
A.1 B.2 C.3 D.4
在4个点中取3个点确定一个圆,关键是
这3个点要不在同一直线上,因此本题
的实质是在A,B,C中找2个点与点
D确定圆.根据题意得出:点D,A,B;点D,A,C;点
D,B,C可以分别确定一个圆.故过这4个点中的任意3
个点,能画圆的个数是3.故选C.
C
导引:
探索新知
总 结
确定一个圆的条件:
(1)已知圆心、半径,可以确定一个圆.
(2)不在同一条直线上的三个点确定一个圆.
典题精讲
1.下列关于确定一个圆的说法中,正确的是( )
A.三个点一定能确定一个圆
B.以已知线段为半径能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
2.已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
C
B
探索新知
3
知识点
三角形的外接圆
试一试:
任意画一个三角形,然后再画出经过三个顶点的圆.
A
B
C
O
探索新知
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
探索新知
例3 如图,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O 的半径.
导引:要求⊙O的半径,已知弦AB的长,需以
AB为边与⊙O的半径(或直径)构成等腰直角三
角形,因此有两个切入点.
方法一:如图1,连接OA,OB,利用圆周角
定理可得∠AOB=2∠C=90°,再利用勾股定
理求出半径;方法二:如图2,作直径AD,连接BD,利用同弧所对的圆周角相等,得∠D=∠C=45°,再利用勾股定理可求出半径.
探索新知
解:方法一:如图1,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图 1
探索新知
方法二:如图2,作直径AD,连接BD,设⊙O的半径为r.
∵AD为⊙O的直径,∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°,
∴BD=AB=4.
在Rt△ABD中,AB2+BD2=AD2,
即42+42=(2r)2,
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
图 2
探索新知
总 结
求三角形的外接圆半径时,最常用的办法是作出圆心与三角形顶点的连线(即半径),延长使这条半径变为直径,将求半径转化为直角三角形中求边的长.
典题精讲
如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心?
如图所示,根据垂径定理的推论,两个直径的交点即为圆心.
探索新知
4
知识点
反证法
思考:经过同一条直线上的三个点能作出一个圆吗?
如图,假设经过同一条直线l上的A,B,C三点可以作一个圆.设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,
而l1⊥l,l2⊥l,这与我们以前学过的“过一点
有且只有一条直线与已知直线垂直”矛盾. 所
以,经过同一条直线上的三个点不能作圆.
探索新知
归 纳
上面证明“经过同一条直线上的三个点不能作圆”的方法与我们以前学过的证明不同,它不是直接从命题的已知得出结论,而是假设命题的结论不成立(即假设经过同一条直线上的三个点可以作一个圆),由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.这种方法叫做反证法.
探索新知
例4 用反证法证明平行线的性质“两直线平行,同位角相等”.
如图,我们要证明:如果AB∥CD,那么∠1=∠2.
假设∠1≠∠2,过点O作直线A′B′,
使∠EOB′=∠2.根据
“同位角相等,两直线平行”,可
得A′B′∥CD.这样,过点O就有
两条直线AB,A′B′都平行于CD,这与平行公理“过
直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,从而∠1=∠2.
证明:
探索新知
总 结
(1)反证法适用情形:①命题的结论的表述为“肯定”或“否定”,且用直接法证较困难;②证明一个定理的逆命题,用直接法证较困难.使用反证法的前提条件是“结论”的反面可列举出来.
(2)反证法使用要经历:反设→归谬→结论这三步,反设是推理归纳的已知条件,即把反设作为已知条件进行推理;归谬是关键,是反证法的核心,其作用是:从命题结论的反面出发,推出与已知事理(定义、公理、定理、已知条件)矛盾;最后说明假设不成立,原结论成立.
典题精讲
1.用反证法证明命题“三角形中必有一个内角小于或等于60°” 时,首先应假设三角形中( )
A.有一个内角大于60° B.有一个内角小于60°
C.每一个内角都大于60° D.每一个内角都小于60°
2.用反证法证明命题“若⊙O的半径为r,点P到圆心的距离为d,且d>r,则点P在⊙O的外部”,应先假设______________________________.
C
点P在⊙O上或点P在⊙O内
学以致用
小试牛刀
1.过点A,B的圆有无数个,这些圆的圆心都在线段AB的_____________上,当圆心O确定之后,OA或OB即为圆的_______.
垂直平分线
半径
2.如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为____.
3.用反证法证明“三角形中至少有一个角不小于60°”第一步假设为:
_______________________________.
18°
三角形中三个角都小于60°
小试牛刀
4.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴
到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则
圆的半径为______cm.
5.已知点P在半径为5的⊙O外,如果设OP=x,那么x的取值范围是
_____.
x>5
小试牛刀
6.已知⊙O的半径为6,A为线段PO的中点,当OP=10时,点A与⊙O
的位置关系为( )
A.在圆上 B.在圆外
C.在圆内 D.不确定
7.在平面直角坐标系xOy中,⊙O的半径为4,点P的坐标为(3,4), 则
点P的位置为( )
A.在⊙O外 B.在⊙O上
C.在⊙O内 D.不确定
C
A
小试牛刀
8.根据下列条件可以确定一个圆的是( )
A.已知圆心 B.已知半径
C.已知直径 D.三个点
9.若⊙O所在平面内一点P到⊙O上的最大距离为3,最小距离为1,
则此圆的半径为( )
A.2或1 B.2或4 C.2 D.1
C
A
小试牛刀
解:(1)答案不唯一,如图所示.
10.如图,在矩形ABCD中,AB=2,AD=4.
(1)以点A为圆心画两个同心圆,使点B在小圆内,点C在大圆外;
小试牛刀
10.如图,在矩形ABCD中,AB=2,AD=4.
(2)以点A为圆心画⊙A,设⊙A的半径为R,若点B,C,D三点中至少有一点在⊙A内,且至少有一点在⊙A外,求R的取值范围.
小试牛刀
解:由SAS可证.
11.如图①,在△ABC中,BA=BC,D是平面内不与点A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
小试牛刀
解: 四边形BECD是菱形.
证明:∵△ABD≌△CBE,∴AD=CE.
∵点D是△ABC的外接圆圆心,
∴DA=DB=DC. 又∵BD=BE,
∴BD=BE=EC=CD,∴四边形BECD是菱形.
11.如图①,在△ABC中,BA=BC,D是平面内不与点A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(2)如图②,当点D是△ABC的外接圆圆心时,请判断四边形BECD的形状,并证明你的结论.
课堂小结
课堂小结
1.点和圆的三种位置关系:设⊙O的半径为r,点P到圆心
的距离为d,则
2.过一点可以作无数个圆.
3.过两点可以作无数个圆.圆心在以已知两点为端点的线
段的垂直平分线上.
4.过三点
5.反证法的证明思想:反设、归谬、结论.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
