冀教版(新)七上-2.7 角的和与差 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)七上-2.7 角的和与差 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:00 | ||
图片预览










文档简介
(共30张PPT)
2.7 角的和与差
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如果两个角的和是平角、直角时,这两个角的关系是怎样的呢?
新课精讲
探索新知
1
知识点
余角和补角的定义
已知∠α和∠β .
如果∠α + ∠β =90°,那么我们就称∠α与∠β互为余角,简称互余.其中∠α (∠β) 叫做∠β(∠α)的余角.
∠α + ∠β =180 °,那么我们就称这两个角互为补角,
简称互补.其中∠α (∠β) 叫做∠β(∠α)的补角.
定义
探索新知
对余角和补角的理解:
(1)互余、互补必须是两个角之间的关系;
(2)互余、互补只与两角的数量关系有关,与位置无关;
(3)∠α的余角可记作90°-∠α,∠α的补角可记作180°-∠α.
探索新知
例1 下列说法正确的有( )
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
B
导引:
主要紧扣锐角、直角、钝角、余角、补角的特征进行判断,除①②不正确外,其他说法都正确.
探索新知
总 结
由于互余的两个角之和为90°,所以这两个角都为锐角;由于互补的两个角之和为180°,所以这两个角为一个锐角一个钝角或两个角都为直角.
典题精讲
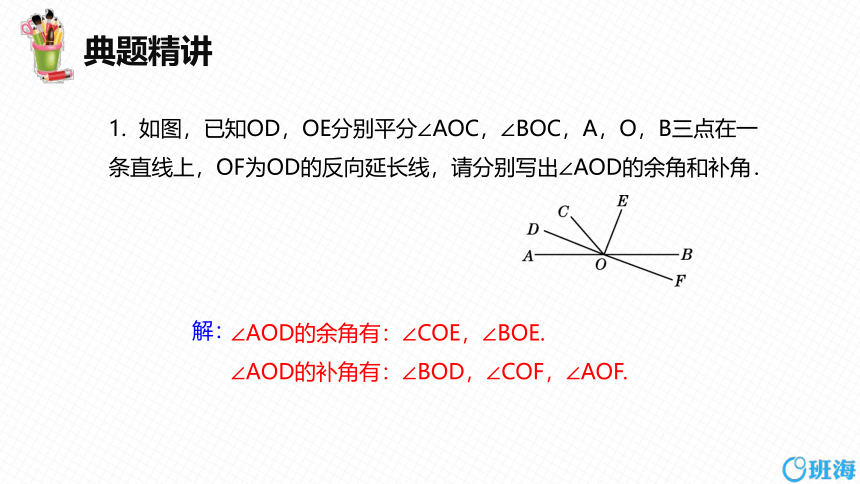
1. 如图,已知OD,OE分别平分∠AOC,∠BOC,A,O,B三点在一条直线上,OF为OD的反向延长线,请分别写出∠AOD的余角和补角.
解:
∠AOD的余角有:∠COE,∠BOE.
∠AOD的补角有:∠BOD,∠COF,∠AOF.
典题精讲
2. 已知∠α=35°,那么∠α的余角等于( )
A. 35° B. 55° C. 65° D. 145°
3. 已知∠α=35°,那么∠α的补角的度数是( )
A. 55° B. 65° C. 145° D. 165°
B
C
探索新知
2
知识点
余角和补角的性质
1. 如果∠α =46°,那么它的余角是多少度,它的补角是多少度?
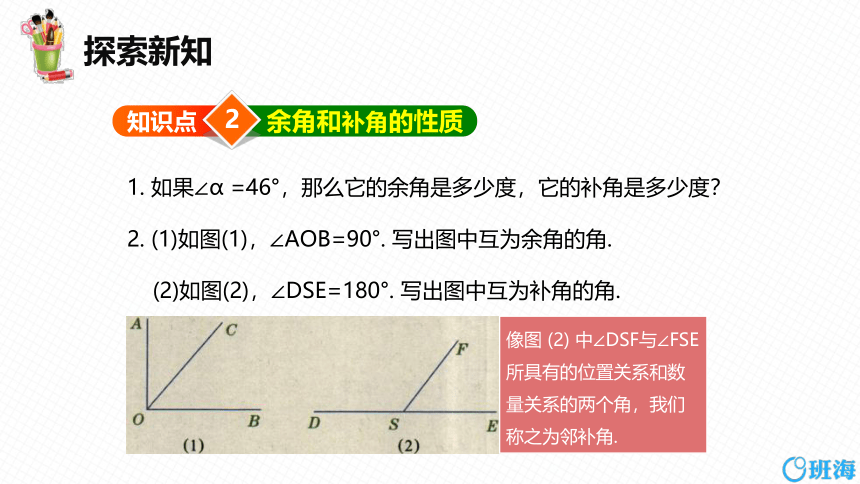
2. (1)如图(1),∠AOB=90°. 写出图中互为余角的角.
(2)如图(2),∠DSE=180°. 写出图中互为补角的角.
像图 (2) 中∠DSF与∠FSE 所具有的位置关系和数量关系的两个角,我们称之为邻补角.
探索新知
1. 如果∠1和∠2都是∠α的余角,那么∠1和∠2相等吗?
2. 如果∠3和∠4都是∠β的补角,那么∠3和∠4相等吗?说明你的理由.
问 题
探索新知
同角(或等角)的余角相等,
同角(或等角)的补角相等.
性质
探索新知
例2 如图,直线AB与∠COD的两边OC,OD分别相交于点E,F,∠1+∠2=180°. 找出图中与∠2相等的角,并说明理由.
导引:
已知∠1+∠2=180°,说明∠2是∠1的补角.根据同角的补角相等,便可确定与∠2相等的角.
探索新知
解:
如图 ,因为∠1+∠3=180°,
∠1+∠2=180°,所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角有∠3,∠4,∠6.
探索新知
总 结
“同角(或等角)的余角相等”“同角(或等角)的补角相等”的实质是等量代换,只不过在特定的背景下使用起来更便捷罢了.
典题精讲
1. 如图,若∠AOB,∠COD都与∠BOC互余,则图中互补的角共有( )
A.1对 B.2对
C.3对 D.4对
B
2. 若∠α+∠β=90°,∠β+∠γ=90°,则∠α与∠γ的关系是( )
A. 互余 B. 互补
C. 相等 D. ∠α=90°+∠γ
C
典题精讲
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A. 同角的余角相等
B. 等角的余角相等
C. 同角的补角相等
D. 等角的补角相等
C
学以致用
小试牛刀
1.下列各图中,∠1与∠2互为余角的是( )
B
小试牛刀
2.下列说法正确的是( )
A.两个锐角一定互余
B.锐角和钝角一定互补
C.互余且相等的两角一定都是45°
D.同一角的余角与它的补角一定相等
C
3.一个角的补角比它的余角( )
A.相等 B.小90° C.大90° D.不确定大小
C
小试牛刀
4.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的
关系是( )
A.互补 B.互余
C.相等 D.无法确定
5.如图所示,点O在直线AE上,OB平分∠AOC,∠BOD=90°,则
∠DOE和∠COB的关系是( )
A.互余 B.互补
C.相等 D.和是钝角
C
A
小试牛刀
6.如图,∠AOB=∠COD=90°,那么∠AOC=∠BOD,这是根据( )
A.直角都相等
B.同角的余角相等
C.同角的补角相等
D.互为余角的两个角相等
B
小试牛刀
7.已知∠1的余角是∠2的补角的 ,并且∠2= ∠1,求∠1+∠2
的度数.
解:由题意得90°- ∠1= (180 °- ∠2),即90°- ∠1 =60 ° - ∠2,所以∠1- ∠2=30°.又因为∠2= ∠1,所以∠1- × ∠1=30°,解得∠1=60°,所以∠2=90°,所以∠1+∠2=60 °+90 °=150 ° .
小试牛刀
8.如图,OD平分∠BOC,OE平分∠AOC,若∠BOC=70 °,∠AOC=50 °.
( 1)求出∠AOB及其补角的度数;
解:( 1)∠AOB=∠AOC+∠BOC=50°+70°=120°.
∠AOB的补角度数为180 °-120 °=60 °.
小试牛刀
8.如图,OD平分∠BOC,OE平分∠AOC,若∠BOC=70 °,∠AOC=50 °.
( 2)求出∠DOC和∠COE的度数,
并判断∠DOE与∠AOB是否互补.
( 2)因为OD,OE分别平分∠BOC,∠AOC,所以∠DOC= ∠BOC=
×70°=35°。∠COE= ∠AOC= ×50°=25°.因为∠DOE=
∠DOC+∠COE,所以∠DOE=35°+25°=60°.因为∠DOE+∠AOB
=60°+120°=180°,所以∠DOE与∠AOB互补.
课堂小结
课堂小结
重要知识点 知识点解析 特别注意的问题
补角 如果两个角的度数之和等于180°(平角),就说这两个角互为补角,简称互补. 补角是两个角之间的关系,一个角不能说互补,三个以上角也不能说互补.
余角 两个角的度数之和等于90°(直角),就说这两个角互为余角,简称互余. 余角是两个角之间的关系,一个角不能说互余,三个以上角也不能说互余.
补角、余角的性质 同角或等角的补角相等;同角或等角的余角相等;同角(或等角)的补角、余角分别相等 成立的条件是:
1.同一个角的补角、余角;2.相等的角的补角、余角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.7 角的和与差
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如果两个角的和是平角、直角时,这两个角的关系是怎样的呢?
新课精讲
探索新知
1
知识点
余角和补角的定义
已知∠α和∠β .
如果∠α + ∠β =90°,那么我们就称∠α与∠β互为余角,简称互余.其中∠α (∠β) 叫做∠β(∠α)的余角.
∠α + ∠β =180 °,那么我们就称这两个角互为补角,
简称互补.其中∠α (∠β) 叫做∠β(∠α)的补角.
定义
探索新知
对余角和补角的理解:
(1)互余、互补必须是两个角之间的关系;
(2)互余、互补只与两角的数量关系有关,与位置无关;
(3)∠α的余角可记作90°-∠α,∠α的补角可记作180°-∠α.
探索新知
例1 下列说法正确的有( )
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
B
导引:
主要紧扣锐角、直角、钝角、余角、补角的特征进行判断,除①②不正确外,其他说法都正确.
探索新知
总 结
由于互余的两个角之和为90°,所以这两个角都为锐角;由于互补的两个角之和为180°,所以这两个角为一个锐角一个钝角或两个角都为直角.
典题精讲
1. 如图,已知OD,OE分别平分∠AOC,∠BOC,A,O,B三点在一条直线上,OF为OD的反向延长线,请分别写出∠AOD的余角和补角.
解:
∠AOD的余角有:∠COE,∠BOE.
∠AOD的补角有:∠BOD,∠COF,∠AOF.
典题精讲
2. 已知∠α=35°,那么∠α的余角等于( )
A. 35° B. 55° C. 65° D. 145°
3. 已知∠α=35°,那么∠α的补角的度数是( )
A. 55° B. 65° C. 145° D. 165°
B
C
探索新知
2
知识点
余角和补角的性质
1. 如果∠α =46°,那么它的余角是多少度,它的补角是多少度?
2. (1)如图(1),∠AOB=90°. 写出图中互为余角的角.
(2)如图(2),∠DSE=180°. 写出图中互为补角的角.
像图 (2) 中∠DSF与∠FSE 所具有的位置关系和数量关系的两个角,我们称之为邻补角.
探索新知
1. 如果∠1和∠2都是∠α的余角,那么∠1和∠2相等吗?
2. 如果∠3和∠4都是∠β的补角,那么∠3和∠4相等吗?说明你的理由.
问 题
探索新知
同角(或等角)的余角相等,
同角(或等角)的补角相等.
性质
探索新知
例2 如图,直线AB与∠COD的两边OC,OD分别相交于点E,F,∠1+∠2=180°. 找出图中与∠2相等的角,并说明理由.
导引:
已知∠1+∠2=180°,说明∠2是∠1的补角.根据同角的补角相等,便可确定与∠2相等的角.
探索新知
解:
如图 ,因为∠1+∠3=180°,
∠1+∠2=180°,所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角有∠3,∠4,∠6.
探索新知
总 结
“同角(或等角)的余角相等”“同角(或等角)的补角相等”的实质是等量代换,只不过在特定的背景下使用起来更便捷罢了.
典题精讲
1. 如图,若∠AOB,∠COD都与∠BOC互余,则图中互补的角共有( )
A.1对 B.2对
C.3对 D.4对
B
2. 若∠α+∠β=90°,∠β+∠γ=90°,则∠α与∠γ的关系是( )
A. 互余 B. 互补
C. 相等 D. ∠α=90°+∠γ
C
典题精讲
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A. 同角的余角相等
B. 等角的余角相等
C. 同角的补角相等
D. 等角的补角相等
C
学以致用
小试牛刀
1.下列各图中,∠1与∠2互为余角的是( )
B
小试牛刀
2.下列说法正确的是( )
A.两个锐角一定互余
B.锐角和钝角一定互补
C.互余且相等的两角一定都是45°
D.同一角的余角与它的补角一定相等
C
3.一个角的补角比它的余角( )
A.相等 B.小90° C.大90° D.不确定大小
C
小试牛刀
4.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的
关系是( )
A.互补 B.互余
C.相等 D.无法确定
5.如图所示,点O在直线AE上,OB平分∠AOC,∠BOD=90°,则
∠DOE和∠COB的关系是( )
A.互余 B.互补
C.相等 D.和是钝角
C
A
小试牛刀
6.如图,∠AOB=∠COD=90°,那么∠AOC=∠BOD,这是根据( )
A.直角都相等
B.同角的余角相等
C.同角的补角相等
D.互为余角的两个角相等
B
小试牛刀
7.已知∠1的余角是∠2的补角的 ,并且∠2= ∠1,求∠1+∠2
的度数.
解:由题意得90°- ∠1= (180 °- ∠2),即90°- ∠1 =60 ° - ∠2,所以∠1- ∠2=30°.又因为∠2= ∠1,所以∠1- × ∠1=30°,解得∠1=60°,所以∠2=90°,所以∠1+∠2=60 °+90 °=150 ° .
小试牛刀
8.如图,OD平分∠BOC,OE平分∠AOC,若∠BOC=70 °,∠AOC=50 °.
( 1)求出∠AOB及其补角的度数;
解:( 1)∠AOB=∠AOC+∠BOC=50°+70°=120°.
∠AOB的补角度数为180 °-120 °=60 °.
小试牛刀
8.如图,OD平分∠BOC,OE平分∠AOC,若∠BOC=70 °,∠AOC=50 °.
( 2)求出∠DOC和∠COE的度数,
并判断∠DOE与∠AOB是否互补.
( 2)因为OD,OE分别平分∠BOC,∠AOC,所以∠DOC= ∠BOC=
×70°=35°。∠COE= ∠AOC= ×50°=25°.因为∠DOE=
∠DOC+∠COE,所以∠DOE=35°+25°=60°.因为∠DOE+∠AOB
=60°+120°=180°,所以∠DOE与∠AOB互补.
课堂小结
课堂小结
重要知识点 知识点解析 特别注意的问题
补角 如果两个角的度数之和等于180°(平角),就说这两个角互为补角,简称互补. 补角是两个角之间的关系,一个角不能说互补,三个以上角也不能说互补.
余角 两个角的度数之和等于90°(直角),就说这两个角互为余角,简称互余. 余角是两个角之间的关系,一个角不能说互余,三个以上角也不能说互余.
补角、余角的性质 同角或等角的补角相等;同角或等角的余角相等;同角(或等角)的补角、余角分别相等 成立的条件是:
1.同一个角的补角、余角;2.相等的角的补角、余角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
