冀教版(新)七上-2.8 平面图形的旋转【优质课件】
文档属性
| 名称 | 冀教版(新)七上-2.8 平面图形的旋转【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:00 | ||
图片预览









文档简介
(共41张PPT)
2.8 平面图形的旋转
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
看左图,飞机的螺旋桨,汽车的轮子,放映机的胶片带动轮,水龙头的开关的运动,有什么共同特点呢?
新课精讲
探索新知
1
知识点
图形的旋转
钟表的指针及风力发电机的叶片在做什么样的运动
探索新知
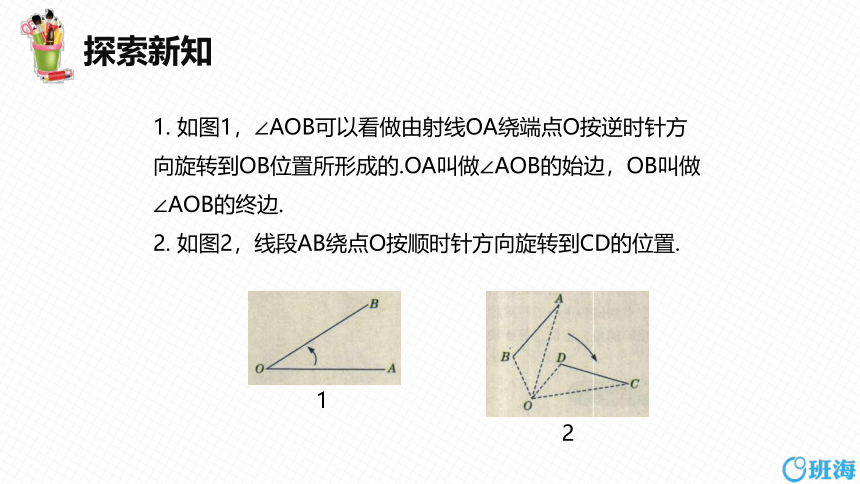
1. 如图1,∠AOB可以看做由射线OA绕端点O按逆时针方向旋转到OB位置所形成的.OA叫做∠AOB的始边,OB叫做∠AOB的终边.
2. 如图2,线段AB绕点O按顺时针方向旋转到CD的位置.
1
2
探索新知
像这样,在平面内,一个图形绕一个定点沿某个方向转过一个角度,这 样的图形运动叫做旋转.
这个定点叫做旋转中心,转过的这个角叫做旋转角.
定义
探索新知
例1 下列运动属于旋转的是( )
A. 羽毛球比赛中,羽毛球在空中的运动
B. 钟摆的摆动
C. 气球升空的运动
D. 一个图形沿某条直线对折的过程
导引:
按旋转的定义判断
B
探索新知
总 结
判断一种运动是否是旋转的前提条件是图形在同一平面内的运动,其次要紧扣旋转的“三要素”,看是否具有:旋转中心、旋转角、旋转方向.
典题精讲
1. 下列现象中,属于旋转的是( )
A. 钟摆的摆动 B. 飞机在飞行 C. 汽车在奔驰 D. 小鸟飞翔
2. 下列现象中,是旋转的是( )
A. 车轮在水平地面上滚动
B. 火车车厢的直线运动
C. 电梯的上下移动
D. 汽车方向盘的转动
A
D
探索新知
2
知识点
旋转中心、旋转角
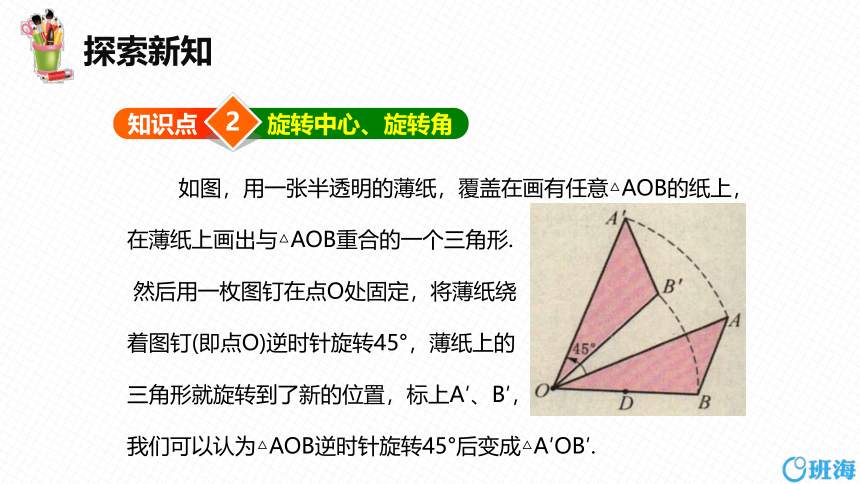
如图,用一张半透明的薄纸,覆盖在画有任意△AOB的纸上,在薄纸上画出与△AOB重合的一个三角形.
然后用一枚图钉在点O处固定,将薄纸绕
着图钉(即点O)逆时针旋转45°,薄纸上的
三角形就旋转到了新的位置,标上A′、B′,
我们可以认为△AOB逆时针旋转45°后变成△A′OB′.
探索新知
我在这样的旋转过程中,你发现了什么?
从图中,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角 .
此时:
点B的对应点是点______;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
∠A的对应角是______;∠B的对应角是______;
旋转中心是点______;旋转的角度是______.
探索新知
1. 旋转的三要素:旋转中心,旋转角,旋转方向.
要点精析:
(1)图形的旋转是由旋转中心、旋转角度及旋转的方向决定的.
(2)旋转中心在整个旋转过程中保持不动.
(3)图形在旋转的过程中,其形状和大小不发生变化,只是位置发生了改变.
探索新知
(4)在旋转的过程中,图形上的每一个点同时按相同的方向旋转相同的角度.
(5)旋转角是大于0°而小于360°的角,旋转的方向通常说顺时针或逆时针,一组对应点与旋转中心的连线所成的角即为旋转角.
(6)旋转中心可以是平面内的任一点.
2. 相关概念:旋转得到的图形能与原图形重合,我们把能够重合的点叫做对应点,能够重合的线段叫做对应线段,能够重合的角叫做对应角.
探索新知
如图, △ABC是等边三角形,D是BC上一点, △ABD经过逆时针旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点, 那么经过上述
旋转后,点M转到了什么位置?
例2
解:
(1)旋转中心是点A.
(2)旋转了 60°.
(3)点M转到了AC的中点位置上.
探索新知
总 结
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
典题精讲
1. 如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是_____,旋转方向是____________,旋转角度是____,点B的对应点是_____.
点A
逆时针方向
45°
点E
典题精讲
2. 如图,三角形AOB绕着点O旋转至三角形A′OB′,此时:
(1)点B的对应点是________;
(2)旋转中心是________,
旋转角为___________________;
(3)∠A的对应角是_______,线段OB的对应线段是__________.
点B′
点O
∠AOA′(或∠BOB ′)
∠A′
线段OB′
典题精讲
3. 如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下
关于旋转中心和对应点的说法正确的是( )
A. 点A是旋转中心,点B和点E是对应点
B. 点C是旋转中心,点B和点D是对应点
C. 点A是旋转中心,点C和点E是对应点
D. 点D是旋转中心,点A和点D是对应点
C
探索新知
如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
例3
探索新知
解:
如图(2),顺时针旋转90°,A′B′与AB互相垂直.
如图(3),逆时针旋转90°,A′′B′′与AB互相垂直.
线段旋转90°后,与原来位置的线段互相垂直.
探索新知
总 结
在旋转中找出旋转中心、旋转角度及方向是研究旋转的基础,在找角度时,也可以采取测量或计算的方法,本题中由于是特殊图形(正方形),角度易算出.
典题精讲
如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P′BA,
则∠PBP′的度数是 ( )
A.45° B.60°
C.90° D.120°
B
探索新知
3
知识点
旋转的性质
1. 如图,已知A,B是射线OM上的两点,且OA=1 cm,OB=2.5 cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点A',B'的位置,请画出点A', B'.
(2)OA和OA' ,OB和OB' 分别有怎样的数量关系?
探索新知
2. 如图,三角形AOB绕点O按顺时针方向旋转后得到三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD分别相等吗?
(2)∠BOD与∠AOC相等吗?
(3)画出点E的对应点F.
探索新知
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:对应点到旋转中心的距离相等;每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
探索新知
如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60° B.105°
C.120° D.135°
例3
导引:
由题意易知,∠CAC′是旋转角,故∠CAC′=60°,所以∠BAC′=∠BAC+∠CAC′=45°+60°=105°.
B
探索新知
总 结
旋转前后的两个图形的形状、大小未发生改变,利用旋转来解决问题时可抓住以下几点:(1)旋转中的变(图形的位置)与不变(图形的形状、大小);(2)旋转前后的对应关系(顶点、边、角);(3)旋转过程中的相等关系.
典题精讲
如图,将三角形ABC绕点C按逆时针方向旋转25°得到三角形DEC,
已知∠A=25°,∠ACE=80°,则∠B=________.
50°
典题精讲
2. 将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,
C,A′三点在同一直线上,如图所示,则∠α的大小是________.
120°
典题精讲
3. 如图,把三角形ABC绕点O按顺时针方向旋转一定角度后成为三角形A′B′C′,则下列各式:①AB=A′B′;②OB=OB′;③∠AOA′=∠COC′;④∠COB=∠A′OC′;⑤∠COA′=∠BOC′,其中成立的有 ( )
A. 2个 B. 3个
C. 4个 D. 5个
B
学以致用
小试牛刀
1.将数字“6”旋转180°, 得到数字"9",将数字"9”旋转180°,得到数字“6",现将数字"69”旋转“180°”,得到的数字是( )
A. 96 B. 69 C. 66 D. 99
2.如图,四边形ABCD经过旋转后与四边形ADEF重合,则下面各角
不是旋转角的是( )
A.∠BAD B.∠CAE
C.∠DAF D.∠CAF
B
D
小试牛刀
3. 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点
B,A,C在同一条直线上,则三角板ABC旋转的角度是( )
A . 60° B . 90°
C.120 ° D . 150°
4. 如图,三角形OAB绕点O逆时针旋转90°到三角形OCD的位置,
已知∠OAD=55°,则∠OAB的度数为( )
A.55° B.45°
C.40° D.35°
D
D
小试牛刀
5.如图,P是等边三角形ABC内一点,且∠PBC=15° ,若将三角形PBC
绕点B按逆时针方向旋转到三角形P'BA的位置,则旋转角为( )
A. 15° B. 45°
C. 60° D. 75°
C
小试牛刀
6.如图,把一块砖ABCD直立于地面上,然后将其轻轻推倒,在这个过
程中,A点保持不动,四边形ABCD旋转到四边形AB'C'D'的位置.
( 1)指出在这个过程中的旋转中心、旋转方向和旋转角度;
( 2)指出图中的对应点和对应线段.
解:( 1)旋转中心是点A,旋转方向是顺时针
方向,旋转角度是90° .
( 2)点A,B,C,D的对应点分别是点A,B',C',D' ;
AB,AD,BC,CD的对应线段分别是AB',AD',B'C',C'D' .
小试牛刀
7.如图,三角形ACD,三角形AEB都是等腰直角三角形,∠CAD=∠EAB = 90°,∠BAC=30",三角形EAC逆时针旋转一定角度后能与三角形BAD重合.
( 1)旋转中心是哪一点?
( 2)旋转了多少度?
( 3)若EC=10cm,则BD等于多少?
( 1)旋转中心是A点.
( 2)旋转了90° .
( 3)因为线段EC和BD是对应线段,所以BD=EC=10cm.
课堂小结
课堂小结
旋转的“三要素”:
旋转中心、旋转方向、旋转角,
图形的旋转由旋转中心、旋转方向和旋转角度决定;
2. 找旋转角的方法:
(1)找出对应点;
(2)连接对应点和旋转中心;
(3)旋转中心和对应点连线的夹角即为旋转角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.8 平面图形的旋转
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
看左图,飞机的螺旋桨,汽车的轮子,放映机的胶片带动轮,水龙头的开关的运动,有什么共同特点呢?
新课精讲
探索新知
1
知识点
图形的旋转
钟表的指针及风力发电机的叶片在做什么样的运动
探索新知
1. 如图1,∠AOB可以看做由射线OA绕端点O按逆时针方向旋转到OB位置所形成的.OA叫做∠AOB的始边,OB叫做∠AOB的终边.
2. 如图2,线段AB绕点O按顺时针方向旋转到CD的位置.
1
2
探索新知
像这样,在平面内,一个图形绕一个定点沿某个方向转过一个角度,这 样的图形运动叫做旋转.
这个定点叫做旋转中心,转过的这个角叫做旋转角.
定义
探索新知
例1 下列运动属于旋转的是( )
A. 羽毛球比赛中,羽毛球在空中的运动
B. 钟摆的摆动
C. 气球升空的运动
D. 一个图形沿某条直线对折的过程
导引:
按旋转的定义判断
B
探索新知
总 结
判断一种运动是否是旋转的前提条件是图形在同一平面内的运动,其次要紧扣旋转的“三要素”,看是否具有:旋转中心、旋转角、旋转方向.
典题精讲
1. 下列现象中,属于旋转的是( )
A. 钟摆的摆动 B. 飞机在飞行 C. 汽车在奔驰 D. 小鸟飞翔
2. 下列现象中,是旋转的是( )
A. 车轮在水平地面上滚动
B. 火车车厢的直线运动
C. 电梯的上下移动
D. 汽车方向盘的转动
A
D
探索新知
2
知识点
旋转中心、旋转角
如图,用一张半透明的薄纸,覆盖在画有任意△AOB的纸上,在薄纸上画出与△AOB重合的一个三角形.
然后用一枚图钉在点O处固定,将薄纸绕
着图钉(即点O)逆时针旋转45°,薄纸上的
三角形就旋转到了新的位置,标上A′、B′,
我们可以认为△AOB逆时针旋转45°后变成△A′OB′.
探索新知
我在这样的旋转过程中,你发现了什么?
从图中,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角 .
此时:
点B的对应点是点______;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
∠A的对应角是______;∠B的对应角是______;
旋转中心是点______;旋转的角度是______.
探索新知
1. 旋转的三要素:旋转中心,旋转角,旋转方向.
要点精析:
(1)图形的旋转是由旋转中心、旋转角度及旋转的方向决定的.
(2)旋转中心在整个旋转过程中保持不动.
(3)图形在旋转的过程中,其形状和大小不发生变化,只是位置发生了改变.
探索新知
(4)在旋转的过程中,图形上的每一个点同时按相同的方向旋转相同的角度.
(5)旋转角是大于0°而小于360°的角,旋转的方向通常说顺时针或逆时针,一组对应点与旋转中心的连线所成的角即为旋转角.
(6)旋转中心可以是平面内的任一点.
2. 相关概念:旋转得到的图形能与原图形重合,我们把能够重合的点叫做对应点,能够重合的线段叫做对应线段,能够重合的角叫做对应角.
探索新知
如图, △ABC是等边三角形,D是BC上一点, △ABD经过逆时针旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点, 那么经过上述
旋转后,点M转到了什么位置?
例2
解:
(1)旋转中心是点A.
(2)旋转了 60°.
(3)点M转到了AC的中点位置上.
探索新知
总 结
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
典题精讲
1. 如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是_____,旋转方向是____________,旋转角度是____,点B的对应点是_____.
点A
逆时针方向
45°
点E
典题精讲
2. 如图,三角形AOB绕着点O旋转至三角形A′OB′,此时:
(1)点B的对应点是________;
(2)旋转中心是________,
旋转角为___________________;
(3)∠A的对应角是_______,线段OB的对应线段是__________.
点B′
点O
∠AOA′(或∠BOB ′)
∠A′
线段OB′
典题精讲
3. 如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下
关于旋转中心和对应点的说法正确的是( )
A. 点A是旋转中心,点B和点E是对应点
B. 点C是旋转中心,点B和点D是对应点
C. 点A是旋转中心,点C和点E是对应点
D. 点D是旋转中心,点A和点D是对应点
C
探索新知
如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
例3
探索新知
解:
如图(2),顺时针旋转90°,A′B′与AB互相垂直.
如图(3),逆时针旋转90°,A′′B′′与AB互相垂直.
线段旋转90°后,与原来位置的线段互相垂直.
探索新知
总 结
在旋转中找出旋转中心、旋转角度及方向是研究旋转的基础,在找角度时,也可以采取测量或计算的方法,本题中由于是特殊图形(正方形),角度易算出.
典题精讲
如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P′BA,
则∠PBP′的度数是 ( )
A.45° B.60°
C.90° D.120°
B
探索新知
3
知识点
旋转的性质
1. 如图,已知A,B是射线OM上的两点,且OA=1 cm,OB=2.5 cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点A',B'的位置,请画出点A', B'.
(2)OA和OA' ,OB和OB' 分别有怎样的数量关系?
探索新知
2. 如图,三角形AOB绕点O按顺时针方向旋转后得到三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD分别相等吗?
(2)∠BOD与∠AOC相等吗?
(3)画出点E的对应点F.
探索新知
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:对应点到旋转中心的距离相等;每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
探索新知
如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60° B.105°
C.120° D.135°
例3
导引:
由题意易知,∠CAC′是旋转角,故∠CAC′=60°,所以∠BAC′=∠BAC+∠CAC′=45°+60°=105°.
B
探索新知
总 结
旋转前后的两个图形的形状、大小未发生改变,利用旋转来解决问题时可抓住以下几点:(1)旋转中的变(图形的位置)与不变(图形的形状、大小);(2)旋转前后的对应关系(顶点、边、角);(3)旋转过程中的相等关系.
典题精讲
如图,将三角形ABC绕点C按逆时针方向旋转25°得到三角形DEC,
已知∠A=25°,∠ACE=80°,则∠B=________.
50°
典题精讲
2. 将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,
C,A′三点在同一直线上,如图所示,则∠α的大小是________.
120°
典题精讲
3. 如图,把三角形ABC绕点O按顺时针方向旋转一定角度后成为三角形A′B′C′,则下列各式:①AB=A′B′;②OB=OB′;③∠AOA′=∠COC′;④∠COB=∠A′OC′;⑤∠COA′=∠BOC′,其中成立的有 ( )
A. 2个 B. 3个
C. 4个 D. 5个
B
学以致用
小试牛刀
1.将数字“6”旋转180°, 得到数字"9",将数字"9”旋转180°,得到数字“6",现将数字"69”旋转“180°”,得到的数字是( )
A. 96 B. 69 C. 66 D. 99
2.如图,四边形ABCD经过旋转后与四边形ADEF重合,则下面各角
不是旋转角的是( )
A.∠BAD B.∠CAE
C.∠DAF D.∠CAF
B
D
小试牛刀
3. 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点
B,A,C在同一条直线上,则三角板ABC旋转的角度是( )
A . 60° B . 90°
C.120 ° D . 150°
4. 如图,三角形OAB绕点O逆时针旋转90°到三角形OCD的位置,
已知∠OAD=55°,则∠OAB的度数为( )
A.55° B.45°
C.40° D.35°
D
D
小试牛刀
5.如图,P是等边三角形ABC内一点,且∠PBC=15° ,若将三角形PBC
绕点B按逆时针方向旋转到三角形P'BA的位置,则旋转角为( )
A. 15° B. 45°
C. 60° D. 75°
C
小试牛刀
6.如图,把一块砖ABCD直立于地面上,然后将其轻轻推倒,在这个过
程中,A点保持不动,四边形ABCD旋转到四边形AB'C'D'的位置.
( 1)指出在这个过程中的旋转中心、旋转方向和旋转角度;
( 2)指出图中的对应点和对应线段.
解:( 1)旋转中心是点A,旋转方向是顺时针
方向,旋转角度是90° .
( 2)点A,B,C,D的对应点分别是点A,B',C',D' ;
AB,AD,BC,CD的对应线段分别是AB',AD',B'C',C'D' .
小试牛刀
7.如图,三角形ACD,三角形AEB都是等腰直角三角形,∠CAD=∠EAB = 90°,∠BAC=30",三角形EAC逆时针旋转一定角度后能与三角形BAD重合.
( 1)旋转中心是哪一点?
( 2)旋转了多少度?
( 3)若EC=10cm,则BD等于多少?
( 1)旋转中心是A点.
( 2)旋转了90° .
( 3)因为线段EC和BD是对应线段,所以BD=EC=10cm.
课堂小结
课堂小结
旋转的“三要素”:
旋转中心、旋转方向、旋转角,
图形的旋转由旋转中心、旋转方向和旋转角度决定;
2. 找旋转角的方法:
(1)找出对应点;
(2)连接对应点和旋转中心;
(3)旋转中心和对应点连线的夹角即为旋转角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
