冀教版(新)七上-3.2 代数式 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)七上-3.2 代数式 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:00 | ||
图片预览











文档简介
(共33张PPT)
3.2 代数式
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
用字母表示数后,现实世界中的数量和数量之间的关系可以用含字母的式子来表示,于是产生了代数式 .
新课精讲
探索新知
1
知识点
用代数式表示含有倍数关系的实际应用
1. 如图所示,已知装满油时,桶和油的质量 一共是a kg;当油用去一半时,桶和油的质量一共是b kg. 当桶里装满油时,设油的质量为c kg.
(1)当桶里装满油时,写出表示桶的质量的代数式.
(2)当油用去一半时,写出表示桶的质量的代数式.
探索新知
2. 已知参加甲、乙两地植树的同学分别为52人和 23人,现从甲、乙
两地共抽调12人到丙地植树. 如果从甲地抽调x人,那么抽调后,
甲、乙两地各剩下多少人?
将表示甲、乙两地剩下人数的代数式填入下表 .
原来人数/人 抽调人数/人 剩下人数/人
甲地 52 x
乙地 23 12-x
探索新知
用代数式表示实际问题中的数量关系的步骤:
(1)要认真审题,弄清问题中的数量关系和运算顺序;
(2)按代数式书写格式的规范书写.
探索新知
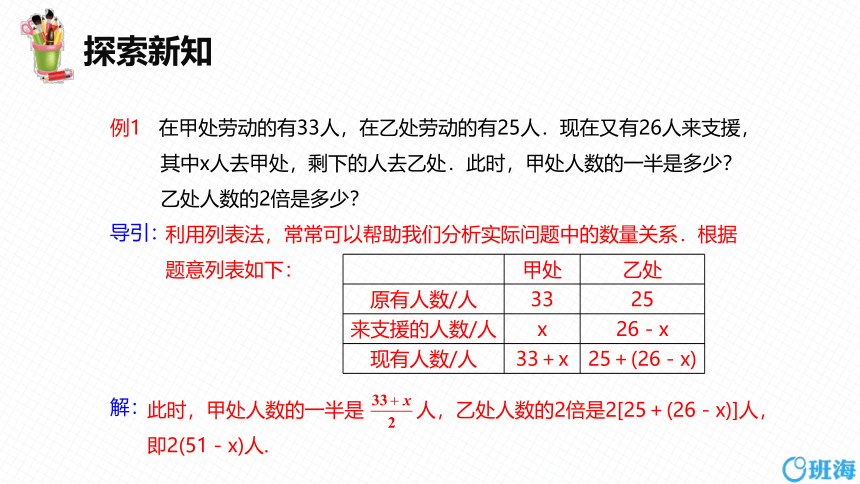
例1 在甲处劳动的有33人,在乙处劳动的有25人.现在又有26人来支援,其中x人去甲处,剩下的人去乙处.此时,甲处人数的一半是多少?乙处人数的2倍是多少?
导引:
利用列表法,常常可以帮助我们分析实际问题中的数量关系.根据题意列表如下:
甲处 乙处
原有人数/人 33 25
来支援的人数/人 x 26-x
现有人数/人 33+x 25+(26-x)
解:
此时,甲处人数的一半是 人,乙处人数的2倍是2[25+(26-x)]人,即2(51-x)人.
探索新知
总 结
解答此类题目通过列表格可以是题目关系直观,便于理解.
典题精讲
1. (1)如果汽车以85 km/h的速度在高速公路上匀速行驶,那么 x h行驶的路程为_____km.
(2)如果某工程队平均每天修路0.8 km,那么x天可以修路_____km.
(3)如果一套学生桌椅的价钱是380元,那么买x套这种学生桌椅需要______元.
(4)如果某期5年期国债的年利率是5.6%,小颖的爷爷买了这期国债x元,那么到期后可得利息________元,本息共为_____________元.
(5)如果一项工程要求30天完成,那么x天后完成了工程量的______.
85x
0.8x
380x
0.056x
(1+ 5.6%)x
典题精讲
2. 一个图书展览馆参加了防火保险,每年的保险费率为0.38%,如果该展览馆的投保价值是b万元,那么投保5年,应交保险费________万元.
3. 一种笔记本的单价是x元,钢笔的单价是y元,李华买这种笔记本4本,钢笔3支,则李华花了( )
A.(x+y)元 B.(3x+4y)元
C.(4x+3y)元 D.(x-y)元
0.019b
C
探索新知
2
知识点
用代数式表示和差关系的实际应用
经过练习,小亮和大华的打字速度都有了提高,小亮的打字速度达到80个/分,大华比小亮每分钟多打10个字.
(1)小亮和大华a min分别能打多少个字?
(2)b min大华比小亮多打多少个字?
(3)将同为c个字的两篇文章分别交给小亮和大华打,如果要求他们同时完成任务,那么小亮比大华要提前多少分钟开始打字?
(4)根据以上问题情境,请你自己提出一个问题并解决.
探索新知
问题中涉及三个基本的量:打字速度、时间、打字的个数. 这些量之间具有怎样的关系?
对每个问题,要表示的是哪个量,用哪些量来表示,怎样表示?
对于上面的问题,可以这样思考和解答:
(1)小亮a min 打的字数就等于80与a的积,即80a个字;大华a min 打的字数就等于(80+10)与a的积,即90a个字.
(2)b min 大华比小亮多打的字数就等于b与10的积,即10b个字.
(3)求小亮要比大华提前多少分钟开始打字,就是求小亮打c个字比大华打c个字多用的时间,也就是求“c除以80的商与c除以(80+10)的商的差”,即
探索新知
例2 从A地乘火车到北京,普通票价格为40元/人,学生票价格为20元/人. 星期日,A地育才学校组织部分师生到天安门广场观看升旗仪式.
(1)如果有教师14人,学生180人,那么买单程火车票共需多少元?
(2)如果有教师x人,学生y人,那么买单程火车票共需多少元?
(3)如果教师人数恰好是学生人数的 ,将教师的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
解:
(3)如果设教师有x人,那么学生有12x人,买单程车票共需 (40x+20×12x)元;如果设学生有y人,那么教师有 人, 买单程车票共需 元,即 元.
(2) (40x+20y)元.
(1) 40×14+20×180=4 160(元).
探索新知
总 结
列代数式时,要准确把握问题中与数量有关的一些词语,因为这些词语的本身就体现了一种运算关系.
1. 已知甲、乙、丙三个数的比为1:2:3. 如果设甲数为x,请表示出甲、乙两数的和减去丙数后的差;如果设丙数为z请表示出甲、丙两数的和减去乙数后的差.
解:
x+2x- 3x=0 z+3z- 2z=2z
2. 为了预防流感,某校积极进行校园环境消毒,购买了甲、乙两种消毒液共100瓶,其中甲种6元/瓶,乙种9元/瓶. 如果设甲种消毒液购买了x瓶,那么购买这两种消毒液共花了多少元?
解:
6x+(100- x)·9=(900-3x) 元.
典题精讲
3. 甲乙两地相距n千米,李师傅驾驶摩托从甲地驶往乙地.原计划每小时行x千米,但实际每小时行40千米(x<40),则从甲地到乙地所需要的时间比原来减少了( )
A. 小时 B. 小时
C. 小时 D. 小时
C
典题精讲
典题精讲
4. 某同学爬一楼梯,从楼下爬到楼顶后立刻返回楼下,已知从楼下到楼顶的路程为s米,同学上楼速度是a米/分,下楼速度是b米/分,则他的平均速度是( )
A. 米/分 B. 米/分
C. 米/分 D. 米/分
D
探索新知
3
知识点
代数式的实际意义
例3 某市的出租车收费标准是:乘车里程不超过3千米的收费是起步价加出租汽车燃油附加费,共8元;乘车里程超过3千米的,除了照收8元以外,超过部分每千米加收1.5元(不足1千米按1千米算).
(1)若某人的乘车里程为15千米,应支付多少元?
(2)若某人的乘车里程为x(x>3,且x为整数)千米,用代数式表示他应支付的费用.
探索新知
导引:
乘车里程超过3千米需付的费用为:8元+超过3千米需付的费用.
(1)因为超过3千米后除了照收8元以外,超过部分每千米加收1.5元(不足1千米按1千米算),所以乘车里程为15千米时,应付费[8+(15-3)×1.5]元;
(2)因为x>3且x为整数,所以应付的费用为[8+(x-3)×1.5]元.
解:
(1)8+(15-3)×1.5=26(元).
(2)(1.5x+3.5)元.
探索新知
总 结
列代数式的关键要分析数量关系,能准确地把文字语言翻译成数学语言.
(1)审题:认真分析问题中有关术语的含义.如和、差、积、商、多、少、几倍、几分之一、增加了、增加到、减少、减少到、扩大、缩小等;
(2)注意问题中语言叙述所表示的运算顺序.如a与b两数和的平方,应为(a+b)2,a,b平方的和,应为a2+b2;
(3)要弄清问题中的层次关系,抓住“的”字的作用. 如用代数式表示:比x与y的差的一半小2m的数. 问题中的“的”字把句子分成三层: ① x与y两数的差; ②差的一半; ③比差的一半小2m.分清层次后很容易得到: (x-y)-2m.注意在书写过程 中层与层之间适当地添加括号;
(4)注意运算的逆向思维.如某数与ab的积为5,则该数为 .问题中出现的是积,而列出的代数式却为商的形式.
典题精讲
某化肥厂10月份的产量比9月份增长了 5%.
(1)如果设9月份的产量为a吨,那么10月份的产量为_______吨.
(2)如果设10月份的产量为b吨,那么9月份的产量为_____吨.
(3)如果设9月份的产量为a吨,那么10月份的产量比9月份的产量实际增加了_______吨.
1.05 a
0.05 a
典题精讲
2. 写代数式的实际意义,就是将代数式中的字母及运算符号赋予具体含义,如3a可解释为:
生活背景:
苹果的价格为3元/千克,买a千克苹果需3a元;
几何背景:
等边三角形的边长为a,这个三角形的周长为3a.
典题精讲
通过阅读以上内容,请分别以生活、几何为背景写出代数式2a+2b的意义.
(1)生活背景:___________________________________________________
_______________________;
(2)几何背景:___________________________________________________.
苹果和梨的价格均为2元/千克,买a千克苹果和b千克梨共需(2a+2b)元
长方形的长为a,宽为b,则长方形的周长为2a+2b
学以致用
小试牛刀
1.七年级有6个班,每个班平均有n个学生,并且七年级一共有30位老师,则七年级共有师生( )
A.(6n+30)人 B.(6n-30)人 C. (30-6n)人 D.6n人
2.某服装店新开张,第一天销售服装a件,第二天比第一天少销售14件,第三天的销售量比第二天的2倍多10件,则第三天销售了( )
A. (2a+10)件 B. (2a+12)件
C. [2(a-14)+10]件 D. [2(a+14)+10]件
A
C
小试牛刀
3.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比
4月份增加了15%,则5月份的产值是( )
A.(a-10%)(a+15%)万元 B.a(1-90%)(1+85%)万元
C.a(1-10%)(1+15%)万元 D.a(1-10%+15%)万元
4.小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,
要串成如图所示的手链,小红购买珠子应该花费( )
A.(3a+4b)元 B. (4a+3b)元
C. 4(a+b)元 D. 3(a+b)元
C
A
小试牛刀
5.火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a,b,c的长方体箱子,按如图所示的方式打包,则打包带的长(不计接头处的长)至少应为( )
A. a+3b+2c B. 2a+4b+6c
C. 4a+10b+4c D. 6a+6b+8c
6.某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为( )
A. 0.2a B. a C. 1.2a D. a+a(1+20%)
B
D
小试牛刀
7.某市的出租车收费标准是:乘车里程不超过3km的收费是起步价加出租汽车燃油附加费,共8元;乘车里程超过3km的,除了照收8元以外,超过部分每千米加收1.5元(不足1km按1km计算).
( 1)若某人的乘车里程为15km,则他应支付多少元?
( 2)若某人的乘车里程为x(x>3,且x为整数)km,用含x的式子表示他应支付的费用.
解:( 1)他应支付[8+(15-3)x1.5]=26(元).
( 2)[8+1.5(x-3)]元.
课堂小结
课堂小结
列代数式,一要注意认真审题,弄清题目中表示的有关数量的关系和运算顺序,要抓住关键词语,如和(加),差(减),积(乘),商(除),大,小,多,少,倍,几分之几,倒数,平方,立方,增加到,增加了等;二要注意题目中的“的”字的作用,列代数式时抓住“的”字把句子分成几个层次,逐层分析,一步步列出代数式;三要注意“除”与“除以”的意义是不同的,“a除b”就是“b除以a”,表示为 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.2 代数式
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
用字母表示数后,现实世界中的数量和数量之间的关系可以用含字母的式子来表示,于是产生了代数式 .
新课精讲
探索新知
1
知识点
用代数式表示含有倍数关系的实际应用
1. 如图所示,已知装满油时,桶和油的质量 一共是a kg;当油用去一半时,桶和油的质量一共是b kg. 当桶里装满油时,设油的质量为c kg.
(1)当桶里装满油时,写出表示桶的质量的代数式.
(2)当油用去一半时,写出表示桶的质量的代数式.
探索新知
2. 已知参加甲、乙两地植树的同学分别为52人和 23人,现从甲、乙
两地共抽调12人到丙地植树. 如果从甲地抽调x人,那么抽调后,
甲、乙两地各剩下多少人?
将表示甲、乙两地剩下人数的代数式填入下表 .
原来人数/人 抽调人数/人 剩下人数/人
甲地 52 x
乙地 23 12-x
探索新知
用代数式表示实际问题中的数量关系的步骤:
(1)要认真审题,弄清问题中的数量关系和运算顺序;
(2)按代数式书写格式的规范书写.
探索新知
例1 在甲处劳动的有33人,在乙处劳动的有25人.现在又有26人来支援,其中x人去甲处,剩下的人去乙处.此时,甲处人数的一半是多少?乙处人数的2倍是多少?
导引:
利用列表法,常常可以帮助我们分析实际问题中的数量关系.根据题意列表如下:
甲处 乙处
原有人数/人 33 25
来支援的人数/人 x 26-x
现有人数/人 33+x 25+(26-x)
解:
此时,甲处人数的一半是 人,乙处人数的2倍是2[25+(26-x)]人,即2(51-x)人.
探索新知
总 结
解答此类题目通过列表格可以是题目关系直观,便于理解.
典题精讲
1. (1)如果汽车以85 km/h的速度在高速公路上匀速行驶,那么 x h行驶的路程为_____km.
(2)如果某工程队平均每天修路0.8 km,那么x天可以修路_____km.
(3)如果一套学生桌椅的价钱是380元,那么买x套这种学生桌椅需要______元.
(4)如果某期5年期国债的年利率是5.6%,小颖的爷爷买了这期国债x元,那么到期后可得利息________元,本息共为_____________元.
(5)如果一项工程要求30天完成,那么x天后完成了工程量的______.
85x
0.8x
380x
0.056x
(1+ 5.6%)x
典题精讲
2. 一个图书展览馆参加了防火保险,每年的保险费率为0.38%,如果该展览馆的投保价值是b万元,那么投保5年,应交保险费________万元.
3. 一种笔记本的单价是x元,钢笔的单价是y元,李华买这种笔记本4本,钢笔3支,则李华花了( )
A.(x+y)元 B.(3x+4y)元
C.(4x+3y)元 D.(x-y)元
0.019b
C
探索新知
2
知识点
用代数式表示和差关系的实际应用
经过练习,小亮和大华的打字速度都有了提高,小亮的打字速度达到80个/分,大华比小亮每分钟多打10个字.
(1)小亮和大华a min分别能打多少个字?
(2)b min大华比小亮多打多少个字?
(3)将同为c个字的两篇文章分别交给小亮和大华打,如果要求他们同时完成任务,那么小亮比大华要提前多少分钟开始打字?
(4)根据以上问题情境,请你自己提出一个问题并解决.
探索新知
问题中涉及三个基本的量:打字速度、时间、打字的个数. 这些量之间具有怎样的关系?
对每个问题,要表示的是哪个量,用哪些量来表示,怎样表示?
对于上面的问题,可以这样思考和解答:
(1)小亮a min 打的字数就等于80与a的积,即80a个字;大华a min 打的字数就等于(80+10)与a的积,即90a个字.
(2)b min 大华比小亮多打的字数就等于b与10的积,即10b个字.
(3)求小亮要比大华提前多少分钟开始打字,就是求小亮打c个字比大华打c个字多用的时间,也就是求“c除以80的商与c除以(80+10)的商的差”,即
探索新知
例2 从A地乘火车到北京,普通票价格为40元/人,学生票价格为20元/人. 星期日,A地育才学校组织部分师生到天安门广场观看升旗仪式.
(1)如果有教师14人,学生180人,那么买单程火车票共需多少元?
(2)如果有教师x人,学生y人,那么买单程火车票共需多少元?
(3)如果教师人数恰好是学生人数的 ,将教师的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
解:
(3)如果设教师有x人,那么学生有12x人,买单程车票共需 (40x+20×12x)元;如果设学生有y人,那么教师有 人, 买单程车票共需 元,即 元.
(2) (40x+20y)元.
(1) 40×14+20×180=4 160(元).
探索新知
总 结
列代数式时,要准确把握问题中与数量有关的一些词语,因为这些词语的本身就体现了一种运算关系.
1. 已知甲、乙、丙三个数的比为1:2:3. 如果设甲数为x,请表示出甲、乙两数的和减去丙数后的差;如果设丙数为z请表示出甲、丙两数的和减去乙数后的差.
解:
x+2x- 3x=0 z+3z- 2z=2z
2. 为了预防流感,某校积极进行校园环境消毒,购买了甲、乙两种消毒液共100瓶,其中甲种6元/瓶,乙种9元/瓶. 如果设甲种消毒液购买了x瓶,那么购买这两种消毒液共花了多少元?
解:
6x+(100- x)·9=(900-3x) 元.
典题精讲
3. 甲乙两地相距n千米,李师傅驾驶摩托从甲地驶往乙地.原计划每小时行x千米,但实际每小时行40千米(x<40),则从甲地到乙地所需要的时间比原来减少了( )
A. 小时 B. 小时
C. 小时 D. 小时
C
典题精讲
典题精讲
4. 某同学爬一楼梯,从楼下爬到楼顶后立刻返回楼下,已知从楼下到楼顶的路程为s米,同学上楼速度是a米/分,下楼速度是b米/分,则他的平均速度是( )
A. 米/分 B. 米/分
C. 米/分 D. 米/分
D
探索新知
3
知识点
代数式的实际意义
例3 某市的出租车收费标准是:乘车里程不超过3千米的收费是起步价加出租汽车燃油附加费,共8元;乘车里程超过3千米的,除了照收8元以外,超过部分每千米加收1.5元(不足1千米按1千米算).
(1)若某人的乘车里程为15千米,应支付多少元?
(2)若某人的乘车里程为x(x>3,且x为整数)千米,用代数式表示他应支付的费用.
探索新知
导引:
乘车里程超过3千米需付的费用为:8元+超过3千米需付的费用.
(1)因为超过3千米后除了照收8元以外,超过部分每千米加收1.5元(不足1千米按1千米算),所以乘车里程为15千米时,应付费[8+(15-3)×1.5]元;
(2)因为x>3且x为整数,所以应付的费用为[8+(x-3)×1.5]元.
解:
(1)8+(15-3)×1.5=26(元).
(2)(1.5x+3.5)元.
探索新知
总 结
列代数式的关键要分析数量关系,能准确地把文字语言翻译成数学语言.
(1)审题:认真分析问题中有关术语的含义.如和、差、积、商、多、少、几倍、几分之一、增加了、增加到、减少、减少到、扩大、缩小等;
(2)注意问题中语言叙述所表示的运算顺序.如a与b两数和的平方,应为(a+b)2,a,b平方的和,应为a2+b2;
(3)要弄清问题中的层次关系,抓住“的”字的作用. 如用代数式表示:比x与y的差的一半小2m的数. 问题中的“的”字把句子分成三层: ① x与y两数的差; ②差的一半; ③比差的一半小2m.分清层次后很容易得到: (x-y)-2m.注意在书写过程 中层与层之间适当地添加括号;
(4)注意运算的逆向思维.如某数与ab的积为5,则该数为 .问题中出现的是积,而列出的代数式却为商的形式.
典题精讲
某化肥厂10月份的产量比9月份增长了 5%.
(1)如果设9月份的产量为a吨,那么10月份的产量为_______吨.
(2)如果设10月份的产量为b吨,那么9月份的产量为_____吨.
(3)如果设9月份的产量为a吨,那么10月份的产量比9月份的产量实际增加了_______吨.
1.05 a
0.05 a
典题精讲
2. 写代数式的实际意义,就是将代数式中的字母及运算符号赋予具体含义,如3a可解释为:
生活背景:
苹果的价格为3元/千克,买a千克苹果需3a元;
几何背景:
等边三角形的边长为a,这个三角形的周长为3a.
典题精讲
通过阅读以上内容,请分别以生活、几何为背景写出代数式2a+2b的意义.
(1)生活背景:___________________________________________________
_______________________;
(2)几何背景:___________________________________________________.
苹果和梨的价格均为2元/千克,买a千克苹果和b千克梨共需(2a+2b)元
长方形的长为a,宽为b,则长方形的周长为2a+2b
学以致用
小试牛刀
1.七年级有6个班,每个班平均有n个学生,并且七年级一共有30位老师,则七年级共有师生( )
A.(6n+30)人 B.(6n-30)人 C. (30-6n)人 D.6n人
2.某服装店新开张,第一天销售服装a件,第二天比第一天少销售14件,第三天的销售量比第二天的2倍多10件,则第三天销售了( )
A. (2a+10)件 B. (2a+12)件
C. [2(a-14)+10]件 D. [2(a+14)+10]件
A
C
小试牛刀
3.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比
4月份增加了15%,则5月份的产值是( )
A.(a-10%)(a+15%)万元 B.a(1-90%)(1+85%)万元
C.a(1-10%)(1+15%)万元 D.a(1-10%+15%)万元
4.小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,
要串成如图所示的手链,小红购买珠子应该花费( )
A.(3a+4b)元 B. (4a+3b)元
C. 4(a+b)元 D. 3(a+b)元
C
A
小试牛刀
5.火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a,b,c的长方体箱子,按如图所示的方式打包,则打包带的长(不计接头处的长)至少应为( )
A. a+3b+2c B. 2a+4b+6c
C. 4a+10b+4c D. 6a+6b+8c
6.某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为( )
A. 0.2a B. a C. 1.2a D. a+a(1+20%)
B
D
小试牛刀
7.某市的出租车收费标准是:乘车里程不超过3km的收费是起步价加出租汽车燃油附加费,共8元;乘车里程超过3km的,除了照收8元以外,超过部分每千米加收1.5元(不足1km按1km计算).
( 1)若某人的乘车里程为15km,则他应支付多少元?
( 2)若某人的乘车里程为x(x>3,且x为整数)km,用含x的式子表示他应支付的费用.
解:( 1)他应支付[8+(15-3)x1.5]=26(元).
( 2)[8+1.5(x-3)]元.
课堂小结
课堂小结
列代数式,一要注意认真审题,弄清题目中表示的有关数量的关系和运算顺序,要抓住关键词语,如和(加),差(减),积(乘),商(除),大,小,多,少,倍,几分之几,倒数,平方,立方,增加到,增加了等;二要注意题目中的“的”字的作用,列代数式时抓住“的”字把句子分成几个层次,逐层分析,一步步列出代数式;三要注意“除”与“除以”的意义是不同的,“a除b”就是“b除以a”,表示为 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
