冀教版(新)七上-3.3代数式的值【优质课件】
文档属性
| 名称 | 冀教版(新)七上-3.3代数式的值【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:00 | ||
图片预览











文档简介
(共37张PPT)
3.3代数式的值
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
据报纸记载,一位医生研究得出父母身高可以预测子女成年后的身高公式:儿子身高是由父母身高的和的一半,再乘以1.08,女儿的身高是父亲身高的0.923倍,再加上母亲身高的和再除以2. 读完上边的内容,你能完成下边的问题吗?
(1)已知父亲身高是a米,母亲身高是b米,成年后儿子和女儿的身高应该怎样利用代数式表示呢?
(2)七年级一班女生小红的父亲身高是1.75米,母亲身高是1.62 米,七年级二班男生小明的父亲身高是1.70米,母亲身高是1.62米,你能预测成年后,小红与小明谁个子更高吗?
(3)想知道你成年后的身高吗?
新课精讲
探索新知
1
知识点
求代数式的值
1. 当n取4,10,13,25等值时,分别代入上面的代数式,计算出代数式4n-4相应的值. 对于n的同一个值,同学们得到的结果都相同吗?
2. 以n=4和n=13为例,说明你是如何算出4n-4的值的.
探索新知
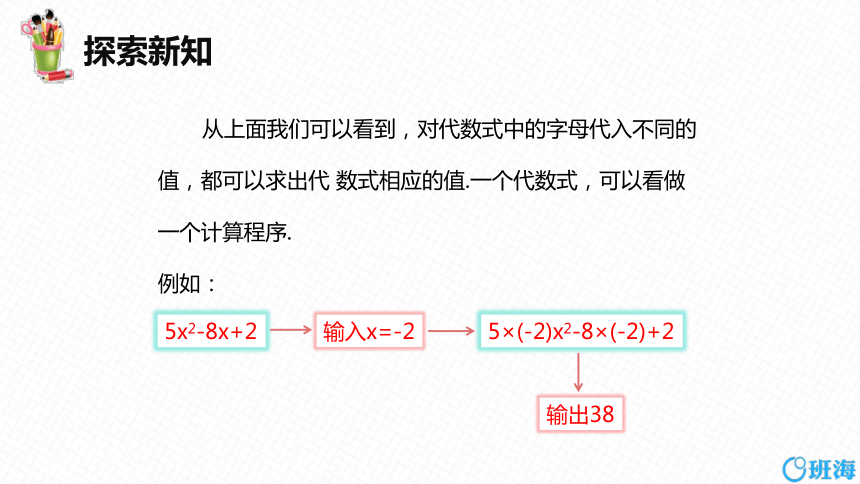
从上面我们可以看到,对代数式中的字母代入不同的值,都可以求出代 数式相应的值.一个代数式,可以看做一个计算程序.
例如:
5x2-8x+2
输入x=-2
5×(-2)x2-8×(-2)+2
输出38
探索新知
问 题
1. 按上面的程序,计算x=3,x=6时的输出值.
2. 任意取x的两个值,请同桌的同学完成上面的求值过程,并相互检查求值过程和结果是否正确.
探索新知
像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值. 这个过程叫做求代数式的值 .
定义
探索新知
例1 根据下面a,b的值,求代数式 的值.
(1) a=2,b=-6; (2) a=-10,b=4 .
解:
(1)当 a=2,b=-6时,
(2) 当 a=-10,b=4时,
探索新知
总 结
用直接代入法求代数式的值可以分三步:
①“当……时”,即指出字母的值;
②“原式=……”,即代入所给字母的值;
③ 计算.
典题精讲
1. 当x=-1,y=3 时,求下列代数式的值:
(1) x3-2y; (2) .
( 1 ) 当x=-1,y=3时,
x3-2y=(-1)3-2×3=
-1-6=-7.
解:
(2)当x=-1,y=3时,
典题精讲
2. 若a=2,b=-1,则a+2b+3的值为( )
A.-1 B.3 C.6 D.5
3. 当1<a<2时,代数式|a-2|+|1-a|的值是( )
A.-1 B.1 C.3 D.-3
B
B
探索新知
2
知识点
整体代入求代数式的值
例2 当代数式x2+3x+5的值为7时,求代数式3x2+9x-2的值.
导引:
由代数式x2+3x+5的值为7,可得x2+3x=2,然后用整体代入法求代数式3x2+9x-2的值.
解:
由代数式x2+3x+5的值为7得x2+3x=2,所以3x2+9x-2=3(x2+3x)-2=4.
探索新知
总 结
要有整体观念,找出所求的代数式与已知关系式之间的关系.
典题精讲
1. 已知代数式 14x+5-21x2的值是-2,求6x2-4x+5的值.
因为14x+5-21x2的值是-2,
所以14x-21x2=-7,即2x-3x2=-1.
所以3x2-2x=1.
所以6x2-4x+5=2×(3x2-2x)+5=7.
解:
典题精讲
2. 已知 ,求 的值.
因为 ,所以 ,
所以原式=2×7- =13.
解:
3. 已知a-b=2,则代数式2a-2b-3的值是( )
A.1 B.2 C.5 D.7
A
探索新知
3
知识点
程序计算求代数式的值
例3 按图所示的程序计算.
(1)若开始输入的n的值为20,则最后输出
的结果y为多少?
(2)若开始输入的n的值为4,则最后输出
的结果y为多少?
探索新知
(1)当n=20时, =190>100,
所以最后输出的结果y为190.
(2)当n=4时, =6<100,
当n=6时, =15<100,
当n=15时, =105>100,
所以最后输出的结果y为105.
解:
探索新知
总 结
解答本题的关键是弄清楚给出的计算程序,利用转化思想求解.
典题精讲
1. 如图所示的运算程序中,若开始输入的x的值为48,请回答下列问题:
(1)第1次输出的结果为_____, 第2次输出的结果为_____;
(2)第2 015次输出的结果为____.
24
12
6
典题精讲
2. 根据如图所示的程序计算,若输入x的值为1,则输出y的值为___.
4
探索新知
4
知识点
实际应用求代数式的值
例4 如图,已知长方体的高为h,底面是边长为a的 正方形.
当h = 3,a = 2时,分别求其体积V和表面积S.
因为 V=a2h ,S=2a2+4ah,
所以当a=2,h=3时,
V=a2h=22×3=12,
S=2a2+4ah=2×22+4×2×3=32.
解:
探索新知
总 结
本题运用了转化思想.把实际要解决的问题转化为求代数式的值的问题.
典题精讲
1. 某种摩托车的行车里程与耗油量有如下关系:
(1)用x表示耗油量,用y表示行车里程,请用含x的代数式表示y;
(2)行车里程为210 km时,耗油量是多少?
(3)如果耗油量为2.7 L,可行多少千米?
行车里程/km 60 120 180 …
耗油量/L 1 2 3 …
典题精讲
(1)y=60x.
(2)当y=210时,210=60x,x=3.5.
即行车里程为210 km时,耗油量是3.5 L.
(3)当x=2.7时,y=60×2.7=162.即耗油量为2.7 L时,可行162 km.
解:
典题精讲
2. 有一根40 cm的金属棒,欲将其截成 x 根 7 cm的小段和 y 根 9 cm的小段,剩余部分作废料处理,若使废料最少,则正整数 x,y 应分别为( )
A.x=1,y=3 B.x=4,y=1
C.x=3,y=2 D.x=2,y=3
C
学以致用
小试牛刀
1.下列求代数式的值,正确的是( )
A.当x=3时,2(x-1) =12
B.当a=-1,b=2时,a +b =3
C.当x=3 时,2x-1=8
D.当m=-3时,m -4m=21
D
小试牛刀
2.当x=-1时,代数式|5x+2|和代数式1-3x的值分别为M,N,则
M,N之间的关系为( )
A.M>N B.M=N
C.M<N D.以上三种情况都有可能
3.当x=1和x=-1时,代数式x -5x +1的值( )
A.互为相反数 B.互为倒数 C.符号相反 D.相等
C
D
小试牛刀
4.已知a-b=2,则代数式2a-2b-3的值是( )
A.1 B.2 C.5 D.7
5.若x -3y-5=0,则6y-2x -6的值( )
A. 4 B.-4 C.16 D.-16
A
D
6.当x= ,y=-5时,求代数式2x -y的值 .
小试牛刀
7. ( 1)根据表中所给a,b的值,计算(a-b) 与a -2ab+b 的值,并将
计算结果填入表中:
( 2)结合(1)的计算结果,你能够得出的结论为 (用含a,b的式子表
示):_________________________ .
( 3)请你利用你发现的结论进行简便运算: 789 -2x789x689+689 .
解:789 -2x789x689+689 =(789-659) =10 000 .
4
4
1
1
25
25
4
4
(a-b) =a -2ab+b
小试牛刀
8. 如图,某长方形广场的四角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形长为a米,宽为b米。
(1)请用代数式表示空地的面积。
(2)若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积。(计算结果保留π)
解:(1) (ab-πr )m .
(2) (60 000-100π)m .
课堂小结
课堂小结
重要知识点 知识点解析 特别注意的问题
代数式的值 用数值代替代数式里的字母,计算后所得的结果叫做代数式的值 字母取不同的值,可能有相同的代数式的值
求代数式的值 1. 求代数式的值的步骤:①先代入,再计算;②先化简,再代入计算. 2. 直接代入:把所给字母的值直接代入代数式求值. 3. 整体代入:把所给简易代数式的值代入繁杂一点的代数式求值. 4. 先化简变形求字母的值、再代入求代数式值 1. 在求代数式的值时,要注意准确代入、正确计算;
2. 当字母的取值是分数或负数的乘方运算时,都要添加必要的括号,把分数或负数括起来.由于代数式的乘号往往被省略,当字母用数值代替时要注意补上乘号.
课堂小结
解题方法小结 1.在代入时一般采用“只代不算”,即只是进行对应替代,不进行计算.
2. 所以求代数式的值时,在代入前,必须写出“当…时”,表示代数式的值是在这种情况下求得的.
3.在解规律探索题或实际生活问题以及信息题时,要认真审题,从特殊到一般地去分析理解,探求解题途径.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.3代数式的值
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
据报纸记载,一位医生研究得出父母身高可以预测子女成年后的身高公式:儿子身高是由父母身高的和的一半,再乘以1.08,女儿的身高是父亲身高的0.923倍,再加上母亲身高的和再除以2. 读完上边的内容,你能完成下边的问题吗?
(1)已知父亲身高是a米,母亲身高是b米,成年后儿子和女儿的身高应该怎样利用代数式表示呢?
(2)七年级一班女生小红的父亲身高是1.75米,母亲身高是1.62 米,七年级二班男生小明的父亲身高是1.70米,母亲身高是1.62米,你能预测成年后,小红与小明谁个子更高吗?
(3)想知道你成年后的身高吗?
新课精讲
探索新知
1
知识点
求代数式的值
1. 当n取4,10,13,25等值时,分别代入上面的代数式,计算出代数式4n-4相应的值. 对于n的同一个值,同学们得到的结果都相同吗?
2. 以n=4和n=13为例,说明你是如何算出4n-4的值的.
探索新知
从上面我们可以看到,对代数式中的字母代入不同的值,都可以求出代 数式相应的值.一个代数式,可以看做一个计算程序.
例如:
5x2-8x+2
输入x=-2
5×(-2)x2-8×(-2)+2
输出38
探索新知
问 题
1. 按上面的程序,计算x=3,x=6时的输出值.
2. 任意取x的两个值,请同桌的同学完成上面的求值过程,并相互检查求值过程和结果是否正确.
探索新知
像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值. 这个过程叫做求代数式的值 .
定义
探索新知
例1 根据下面a,b的值,求代数式 的值.
(1) a=2,b=-6; (2) a=-10,b=4 .
解:
(1)当 a=2,b=-6时,
(2) 当 a=-10,b=4时,
探索新知
总 结
用直接代入法求代数式的值可以分三步:
①“当……时”,即指出字母的值;
②“原式=……”,即代入所给字母的值;
③ 计算.
典题精讲
1. 当x=-1,y=3 时,求下列代数式的值:
(1) x3-2y; (2) .
( 1 ) 当x=-1,y=3时,
x3-2y=(-1)3-2×3=
-1-6=-7.
解:
(2)当x=-1,y=3时,
典题精讲
2. 若a=2,b=-1,则a+2b+3的值为( )
A.-1 B.3 C.6 D.5
3. 当1<a<2时,代数式|a-2|+|1-a|的值是( )
A.-1 B.1 C.3 D.-3
B
B
探索新知
2
知识点
整体代入求代数式的值
例2 当代数式x2+3x+5的值为7时,求代数式3x2+9x-2的值.
导引:
由代数式x2+3x+5的值为7,可得x2+3x=2,然后用整体代入法求代数式3x2+9x-2的值.
解:
由代数式x2+3x+5的值为7得x2+3x=2,所以3x2+9x-2=3(x2+3x)-2=4.
探索新知
总 结
要有整体观念,找出所求的代数式与已知关系式之间的关系.
典题精讲
1. 已知代数式 14x+5-21x2的值是-2,求6x2-4x+5的值.
因为14x+5-21x2的值是-2,
所以14x-21x2=-7,即2x-3x2=-1.
所以3x2-2x=1.
所以6x2-4x+5=2×(3x2-2x)+5=7.
解:
典题精讲
2. 已知 ,求 的值.
因为 ,所以 ,
所以原式=2×7- =13.
解:
3. 已知a-b=2,则代数式2a-2b-3的值是( )
A.1 B.2 C.5 D.7
A
探索新知
3
知识点
程序计算求代数式的值
例3 按图所示的程序计算.
(1)若开始输入的n的值为20,则最后输出
的结果y为多少?
(2)若开始输入的n的值为4,则最后输出
的结果y为多少?
探索新知
(1)当n=20时, =190>100,
所以最后输出的结果y为190.
(2)当n=4时, =6<100,
当n=6时, =15<100,
当n=15时, =105>100,
所以最后输出的结果y为105.
解:
探索新知
总 结
解答本题的关键是弄清楚给出的计算程序,利用转化思想求解.
典题精讲
1. 如图所示的运算程序中,若开始输入的x的值为48,请回答下列问题:
(1)第1次输出的结果为_____, 第2次输出的结果为_____;
(2)第2 015次输出的结果为____.
24
12
6
典题精讲
2. 根据如图所示的程序计算,若输入x的值为1,则输出y的值为___.
4
探索新知
4
知识点
实际应用求代数式的值
例4 如图,已知长方体的高为h,底面是边长为a的 正方形.
当h = 3,a = 2时,分别求其体积V和表面积S.
因为 V=a2h ,S=2a2+4ah,
所以当a=2,h=3时,
V=a2h=22×3=12,
S=2a2+4ah=2×22+4×2×3=32.
解:
探索新知
总 结
本题运用了转化思想.把实际要解决的问题转化为求代数式的值的问题.
典题精讲
1. 某种摩托车的行车里程与耗油量有如下关系:
(1)用x表示耗油量,用y表示行车里程,请用含x的代数式表示y;
(2)行车里程为210 km时,耗油量是多少?
(3)如果耗油量为2.7 L,可行多少千米?
行车里程/km 60 120 180 …
耗油量/L 1 2 3 …
典题精讲
(1)y=60x.
(2)当y=210时,210=60x,x=3.5.
即行车里程为210 km时,耗油量是3.5 L.
(3)当x=2.7时,y=60×2.7=162.即耗油量为2.7 L时,可行162 km.
解:
典题精讲
2. 有一根40 cm的金属棒,欲将其截成 x 根 7 cm的小段和 y 根 9 cm的小段,剩余部分作废料处理,若使废料最少,则正整数 x,y 应分别为( )
A.x=1,y=3 B.x=4,y=1
C.x=3,y=2 D.x=2,y=3
C
学以致用
小试牛刀
1.下列求代数式的值,正确的是( )
A.当x=3时,2(x-1) =12
B.当a=-1,b=2时,a +b =3
C.当x=3 时,2x-1=8
D.当m=-3时,m -4m=21
D
小试牛刀
2.当x=-1时,代数式|5x+2|和代数式1-3x的值分别为M,N,则
M,N之间的关系为( )
A.M>N B.M=N
C.M<N D.以上三种情况都有可能
3.当x=1和x=-1时,代数式x -5x +1的值( )
A.互为相反数 B.互为倒数 C.符号相反 D.相等
C
D
小试牛刀
4.已知a-b=2,则代数式2a-2b-3的值是( )
A.1 B.2 C.5 D.7
5.若x -3y-5=0,则6y-2x -6的值( )
A. 4 B.-4 C.16 D.-16
A
D
6.当x= ,y=-5时,求代数式2x -y的值 .
小试牛刀
7. ( 1)根据表中所给a,b的值,计算(a-b) 与a -2ab+b 的值,并将
计算结果填入表中:
( 2)结合(1)的计算结果,你能够得出的结论为 (用含a,b的式子表
示):_________________________ .
( 3)请你利用你发现的结论进行简便运算: 789 -2x789x689+689 .
解:789 -2x789x689+689 =(789-659) =10 000 .
4
4
1
1
25
25
4
4
(a-b) =a -2ab+b
小试牛刀
8. 如图,某长方形广场的四角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形长为a米,宽为b米。
(1)请用代数式表示空地的面积。
(2)若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积。(计算结果保留π)
解:(1) (ab-πr )m .
(2) (60 000-100π)m .
课堂小结
课堂小结
重要知识点 知识点解析 特别注意的问题
代数式的值 用数值代替代数式里的字母,计算后所得的结果叫做代数式的值 字母取不同的值,可能有相同的代数式的值
求代数式的值 1. 求代数式的值的步骤:①先代入,再计算;②先化简,再代入计算. 2. 直接代入:把所给字母的值直接代入代数式求值. 3. 整体代入:把所给简易代数式的值代入繁杂一点的代数式求值. 4. 先化简变形求字母的值、再代入求代数式值 1. 在求代数式的值时,要注意准确代入、正确计算;
2. 当字母的取值是分数或负数的乘方运算时,都要添加必要的括号,把分数或负数括起来.由于代数式的乘号往往被省略,当字母用数值代替时要注意补上乘号.
课堂小结
解题方法小结 1.在代入时一般采用“只代不算”,即只是进行对应替代,不进行计算.
2. 所以求代数式的值时,在代入前,必须写出“当…时”,表示代数式的值是在这种情况下求得的.
3.在解规律探索题或实际生活问题以及信息题时,要认真审题,从特殊到一般地去分析理解,探求解题途径.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
