冀教版(新)七上-5.2 等式的基本性质【优质课件】
文档属性
| 名称 | 冀教版(新)七上-5.2 等式的基本性质【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:00 | ||
图片预览











文档简介
(共39张PPT)
5.2 等式的基本性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
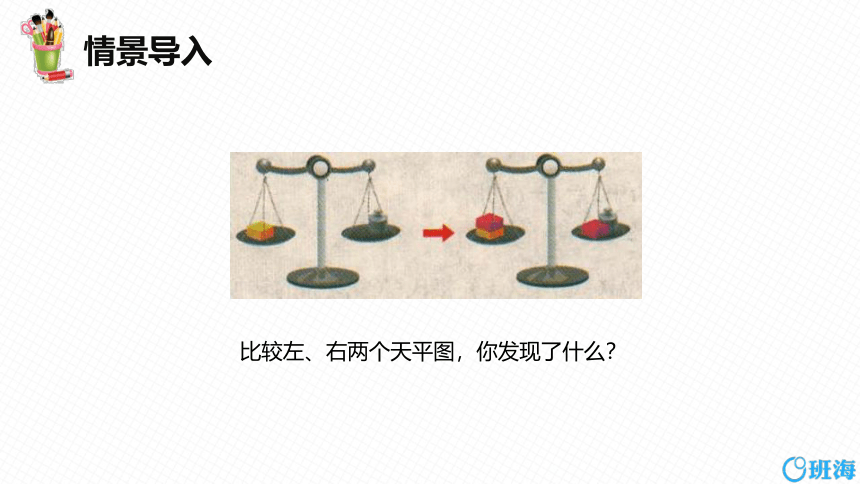
情景导入
比较左、右两个天平图,你发现了什么?
新课精讲
探索新知
1
知识点
等式的性质1
观察下图,并完成其中的填空. 图中的字母表示相应物品的质量,两图中天平均保持平衡.
你从上述过程中发现了等式的哪些性质?怎样用字母表示数来表示等式的性质?
探索新知
总 结
等式的性质1
等式的两边加上(或减去)同一个数或同一个整式,
结果仍是等式,即
如果a=b,那么a±c=b±c.
探索新知
例1 解方程x+3=8.
方程两边都减去3,得 x+3-3= 8-3 .
所以 x=8-3,
即 x=5.
解:
探索新知
总 结
等式变形时,必须根据等式的基本性质1,等式两边同时进行完全相同的运算,等式才成立,否则相等关系就会被破坏.
典题精讲
等式两边加(或_____)同一个_____(或_______),结果仍相等;用字
母表示:如果a=b,那么a±c=______.
2. 已知方程x-2y+3=8,则整式x-2y的值为( )
A.5 B.10
C.12 D.15
减
数
整式
b±c
A
典题精讲
3. 如果x+4=6,那么x=____,理由________________________________
_______.
根据等式的性质1 ,两边同时减 去4得
2
探索新知
2
知识点
等式的性质2
观察下图,并完成其中的填空.图中的字母表示相应物品的质量,两图中天平均保持平衡.
你从上述过程中发现了等式的哪些性质?怎样用字母表示数来表示等式的性质?
探索新知
总 结
等式的性质2
等式的两边乘或除以同一个数或式(除数不能为0),
所得结果仍是等式.即
如果 a=b,那么 ac=bc,或 (c≠0).
例2 根据等式的基本性质填空,并在后面的括号内填上变形的根据 .
(1)如果4x=x-2,那么4x-____=-2 ( );
(2)如果2x+9=1,那么2x=1-____ ( );
(3)如果- = ,那么x=____ ( );
(4)如果0.4a=3b,那么a=____ ( ).
探索新知
x
等式的基本性质1
9
等式的基本性质1
等式的基本性质2
等式的基本性质2
探索新知
(1)中方程的右边由x-2到-2,减了x,所以左边也要减x;
(2)中方程的左边由2x+9到2x,减了9,所以右边也要减9;
(3)中方程的左边由- 到x,乘了-3,所以右边也要乘-3;
(4)中方程的左边由0.4a到a除以了0.4,所以右边
也要除以0.4,即乘 .
导引:
典题精讲
1. 下列等式变形正确的是( )
A.由- x= y,得x=2y
B.由3x-2=2x+2,得x=4
C.由2x-3=3x,得x=3
D.由3x-6=7,得3x=7-6
B
典题精讲
2. 等式2x-y=10变形为-4x+2y=20的依据是等式的性质____,
它是将等式的两边____________.
2
同时乘-2
3. 下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 -1=x,那么2x+1-1=3x
B
探索新知
3
知识点
利用等式的性质变形
如图所示,天平架是平衡的.如果一个黄砝码的质量为1g,一个蓝砝码的质量为xg,请你观察下面的操作过程,并说出1个蓝砝码的质量是多少克.
天平两边同时取走一个黄砝码
图中的平衡现象,用方程可表示为
3x+1= x+5.
方程两边同时减去1
探索新知
天平两边同时取走一个蓝砝码
天平两边各取走一般砝码
方程变为
3x+1-1= x+5-1
即3x= x+4.
方程两边同时减去x
方程变为
3x-x= x+4-x
即2x=4.
方程变为
即x=2.
方程两边同时除以2
探索新知
总 结
方程是等式,根据等式的性质可以求方程的解 .
探索新知
利用等式的两个基本性质进行等式变形时,应分析变形前、后式子的区别,发生加、减变形根据等式的性质1,发生乘除变形的根据等式的性质2.
探索新知
例3 解方程:3+8x=-6x-11.
解以x为未知数的方程,就是把方程逐步化为x=a(常数)的形式,所以先消去左边的常数项,
再消去右边的含未知数的项.
导引:
两边同时减3,整理得
8x=-6x-14.
两边同时加6x,整理得
14x=-14.
两边同时除以14,得x=-1.
解:
探索新知
总 结
利用等式的基本性质解一元一次方程的一般步骤:
首先运用等式的基本性质1,将方程逐步转化为左边只有含未知数的项,右边只有常数项,即ax=b(a≠0)的形式;其次运用等式的基本性质2,将x的系数化为1,即x= (a≠0).运用等式的基本性质时要注意:(1)变形过程务必是从一个方程变换到另一个方程,切不可连等.(2)运用等式的基本性质1不能漏边,运用等式的基本性质2不能漏项.
典题精讲
1. 解方程:
(1)2x-3=8+x; (2)- x+3=1 .
(1)2x-3=8+x,
两边同时减x,得x-3=8.
两边同时加3,得x=11.
解:
(2)- x+3=1,
两边同时减3,得- x=-2.
两边同时除以- ,得x=8.
解:
2. 在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明是根据等式的哪一条性质以及是怎样变形的.
(1)如果 ,那么x=_____,根据_____________________________________;
(2)如果-9x=9y,那么x=____,根据_______________________________________;
(3)如果 ,那么x=___,根据______________________________________;
(4)如果x=3x+2,那么x=____,根据________________________________________ ___________________________________________________.
典题精讲
-2y
等式的性质2,将等式的两边都乘-10
-y
等式的性质2,将等式的两边都除以-9
等式的性质1,将等式的两边都加上
4
-1
等式的性质1和等式的性质2,将等式的两边都减去3x,然后再将等式两边同时除以-2
典题精讲
3. 下列根据等式的性质变形正确的是( )
A.由- x= y,得x=2y
B.由3x-2=2x+2,得x=4
C.由2x-3=3x,得x=3
D.由3x-5=7,得3x=7-5
B
学以致用
小试牛刀
1.等式两边同时加(或减)________________,所得结果仍是_______;即如果a=b,那么____________.
2.已知a=-2,则代数式a+1的值为( )
A.-3 B.-2 C.-1 D.1
同一个代数式
等式
a±c=b±c
C
3.等式两边同时乘__________,或除以同一个不为0的数,所得结果仍是等式,即如果a=b,那么________;如果a=b,c≠0,那么________.
在运用等式的基本性质2时,应注意:等式的两边除以的这个数不为0.
同一个数
ac=bc
小试牛刀
4.如果a+3=0,那么a的值是( )
A.3 B.-3
C. D.
B
5.下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
C
小试牛刀
6.利用等式的基本性质2,不能将下列等式直接变形为x=a的形式的是( )
A . x=0 B.2x=b C.-3x= D.ax=b
D
7.设x,y,c是有理数,( )
A.若x=y,则x+c=y-c B.若x=y,则xc=yc
C.若x=y,则 D.若 ,则2x=3y
B
小试牛刀
8.利用等式的基本性质解方程 +1=2的结果是( )
A.x=2 B.x=-2
C.x=4 D.x=-4
A
9.若x= ,y=4,则代数式3x+y-3的值是( )
A.-6 B.0
C.2 D.6
B
小试牛刀
解:(2)方程两边同时减9,
得-4+ x=- y,
即 y=-4+ x.
方程两边同时乘 ,得y=7- x.
10.已知5+ x=9- y.
(1)用含y的式子表示x; (2)用含x的式子表示y .
解:(1)方程两边同时减5,
得 x=4- y .
方程两边同时乘 ,
得x=14-2y .
小试牛刀
11.解下列方程:
(1)x+5=8 ; (2)-2- x=2;
解:(1)方程两边同时减5,
得x+5-5=8-5,
即x=3.
解:(2)方程两边同时加2,
得-2- x+2=2+2,
即- x=4.
方程两边同时乘-4,得x=-16.
小试牛刀
(3)6x-2=0 ; (4)3(-x+1)=-12 .
解:(4)方程两边同时除以3,
得-x+1=-4.
方程两边同时减1,
得-x=-5,所以x=5.
解:(3)方程两边同时加2,
得6x=2.
方程两边同时除以6,
得x= .
小试牛刀
12.先阅读下面例题的解答过程,再解答后面的题目.
例:已知9-6y-4y2=7,求2y2+3y+7的值.
解:由9-6y-4y2=7,得-6y-4y2=7-9,
即6y+4y2=2,所以2y2+3y=1,所以2y2+3y+7=8.
题目:已知14a-5-21b2=9,求6b2-4a+5的值.
解:由14a-5-21b2=9,得14a-21b2=9+5,
即14a-21b2=14 . 所以3b2-2a=-2 .
所以6b2-4a+5=2(3b2-2a)+5=2×(-2)+5=1 .
小试牛刀
13.能不能从(a+3)x=b-1得到x= ,为什么?反过来,能不能从x= 得到(a+3)x=b-1,为什么?
解:不能从(a+3)x=b-1得到x= ,因为a+3有可能为0,而0不能作为除数;能从x=得到(a+3)x=b-1,因为当x= 时,a+3作为除数,说明a+3的值不为0,再根据等式的基本性质2,就能得到(a+3)x=b-1.
课堂小结
课堂小结
利用等式的基本性质变形的过程是由一个等式变形到另一个等式的过程,变形时应注意:
(1)等式两边都要参与运算,并且进行的是同一种运算;
(2)等式两边加减乘除的数或整式一定是同一个数或同一个整式;
(3)除以的数(或整式)不能为0.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.2 等式的基本性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
比较左、右两个天平图,你发现了什么?
新课精讲
探索新知
1
知识点
等式的性质1
观察下图,并完成其中的填空. 图中的字母表示相应物品的质量,两图中天平均保持平衡.
你从上述过程中发现了等式的哪些性质?怎样用字母表示数来表示等式的性质?
探索新知
总 结
等式的性质1
等式的两边加上(或减去)同一个数或同一个整式,
结果仍是等式,即
如果a=b,那么a±c=b±c.
探索新知
例1 解方程x+3=8.
方程两边都减去3,得 x+3-3= 8-3 .
所以 x=8-3,
即 x=5.
解:
探索新知
总 结
等式变形时,必须根据等式的基本性质1,等式两边同时进行完全相同的运算,等式才成立,否则相等关系就会被破坏.
典题精讲
等式两边加(或_____)同一个_____(或_______),结果仍相等;用字
母表示:如果a=b,那么a±c=______.
2. 已知方程x-2y+3=8,则整式x-2y的值为( )
A.5 B.10
C.12 D.15
减
数
整式
b±c
A
典题精讲
3. 如果x+4=6,那么x=____,理由________________________________
_______.
根据等式的性质1 ,两边同时减 去4得
2
探索新知
2
知识点
等式的性质2
观察下图,并完成其中的填空.图中的字母表示相应物品的质量,两图中天平均保持平衡.
你从上述过程中发现了等式的哪些性质?怎样用字母表示数来表示等式的性质?
探索新知
总 结
等式的性质2
等式的两边乘或除以同一个数或式(除数不能为0),
所得结果仍是等式.即
如果 a=b,那么 ac=bc,或 (c≠0).
例2 根据等式的基本性质填空,并在后面的括号内填上变形的根据 .
(1)如果4x=x-2,那么4x-____=-2 ( );
(2)如果2x+9=1,那么2x=1-____ ( );
(3)如果- = ,那么x=____ ( );
(4)如果0.4a=3b,那么a=____ ( ).
探索新知
x
等式的基本性质1
9
等式的基本性质1
等式的基本性质2
等式的基本性质2
探索新知
(1)中方程的右边由x-2到-2,减了x,所以左边也要减x;
(2)中方程的左边由2x+9到2x,减了9,所以右边也要减9;
(3)中方程的左边由- 到x,乘了-3,所以右边也要乘-3;
(4)中方程的左边由0.4a到a除以了0.4,所以右边
也要除以0.4,即乘 .
导引:
典题精讲
1. 下列等式变形正确的是( )
A.由- x= y,得x=2y
B.由3x-2=2x+2,得x=4
C.由2x-3=3x,得x=3
D.由3x-6=7,得3x=7-6
B
典题精讲
2. 等式2x-y=10变形为-4x+2y=20的依据是等式的性质____,
它是将等式的两边____________.
2
同时乘-2
3. 下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 -1=x,那么2x+1-1=3x
B
探索新知
3
知识点
利用等式的性质变形
如图所示,天平架是平衡的.如果一个黄砝码的质量为1g,一个蓝砝码的质量为xg,请你观察下面的操作过程,并说出1个蓝砝码的质量是多少克.
天平两边同时取走一个黄砝码
图中的平衡现象,用方程可表示为
3x+1= x+5.
方程两边同时减去1
探索新知
天平两边同时取走一个蓝砝码
天平两边各取走一般砝码
方程变为
3x+1-1= x+5-1
即3x= x+4.
方程两边同时减去x
方程变为
3x-x= x+4-x
即2x=4.
方程变为
即x=2.
方程两边同时除以2
探索新知
总 结
方程是等式,根据等式的性质可以求方程的解 .
探索新知
利用等式的两个基本性质进行等式变形时,应分析变形前、后式子的区别,发生加、减变形根据等式的性质1,发生乘除变形的根据等式的性质2.
探索新知
例3 解方程:3+8x=-6x-11.
解以x为未知数的方程,就是把方程逐步化为x=a(常数)的形式,所以先消去左边的常数项,
再消去右边的含未知数的项.
导引:
两边同时减3,整理得
8x=-6x-14.
两边同时加6x,整理得
14x=-14.
两边同时除以14,得x=-1.
解:
探索新知
总 结
利用等式的基本性质解一元一次方程的一般步骤:
首先运用等式的基本性质1,将方程逐步转化为左边只有含未知数的项,右边只有常数项,即ax=b(a≠0)的形式;其次运用等式的基本性质2,将x的系数化为1,即x= (a≠0).运用等式的基本性质时要注意:(1)变形过程务必是从一个方程变换到另一个方程,切不可连等.(2)运用等式的基本性质1不能漏边,运用等式的基本性质2不能漏项.
典题精讲
1. 解方程:
(1)2x-3=8+x; (2)- x+3=1 .
(1)2x-3=8+x,
两边同时减x,得x-3=8.
两边同时加3,得x=11.
解:
(2)- x+3=1,
两边同时减3,得- x=-2.
两边同时除以- ,得x=8.
解:
2. 在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明是根据等式的哪一条性质以及是怎样变形的.
(1)如果 ,那么x=_____,根据_____________________________________;
(2)如果-9x=9y,那么x=____,根据_______________________________________;
(3)如果 ,那么x=___,根据______________________________________;
(4)如果x=3x+2,那么x=____,根据________________________________________ ___________________________________________________.
典题精讲
-2y
等式的性质2,将等式的两边都乘-10
-y
等式的性质2,将等式的两边都除以-9
等式的性质1,将等式的两边都加上
4
-1
等式的性质1和等式的性质2,将等式的两边都减去3x,然后再将等式两边同时除以-2
典题精讲
3. 下列根据等式的性质变形正确的是( )
A.由- x= y,得x=2y
B.由3x-2=2x+2,得x=4
C.由2x-3=3x,得x=3
D.由3x-5=7,得3x=7-5
B
学以致用
小试牛刀
1.等式两边同时加(或减)________________,所得结果仍是_______;即如果a=b,那么____________.
2.已知a=-2,则代数式a+1的值为( )
A.-3 B.-2 C.-1 D.1
同一个代数式
等式
a±c=b±c
C
3.等式两边同时乘__________,或除以同一个不为0的数,所得结果仍是等式,即如果a=b,那么________;如果a=b,c≠0,那么________.
在运用等式的基本性质2时,应注意:等式的两边除以的这个数不为0.
同一个数
ac=bc
小试牛刀
4.如果a+3=0,那么a的值是( )
A.3 B.-3
C. D.
B
5.下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
C
小试牛刀
6.利用等式的基本性质2,不能将下列等式直接变形为x=a的形式的是( )
A . x=0 B.2x=b C.-3x= D.ax=b
D
7.设x,y,c是有理数,( )
A.若x=y,则x+c=y-c B.若x=y,则xc=yc
C.若x=y,则 D.若 ,则2x=3y
B
小试牛刀
8.利用等式的基本性质解方程 +1=2的结果是( )
A.x=2 B.x=-2
C.x=4 D.x=-4
A
9.若x= ,y=4,则代数式3x+y-3的值是( )
A.-6 B.0
C.2 D.6
B
小试牛刀
解:(2)方程两边同时减9,
得-4+ x=- y,
即 y=-4+ x.
方程两边同时乘 ,得y=7- x.
10.已知5+ x=9- y.
(1)用含y的式子表示x; (2)用含x的式子表示y .
解:(1)方程两边同时减5,
得 x=4- y .
方程两边同时乘 ,
得x=14-2y .
小试牛刀
11.解下列方程:
(1)x+5=8 ; (2)-2- x=2;
解:(1)方程两边同时减5,
得x+5-5=8-5,
即x=3.
解:(2)方程两边同时加2,
得-2- x+2=2+2,
即- x=4.
方程两边同时乘-4,得x=-16.
小试牛刀
(3)6x-2=0 ; (4)3(-x+1)=-12 .
解:(4)方程两边同时除以3,
得-x+1=-4.
方程两边同时减1,
得-x=-5,所以x=5.
解:(3)方程两边同时加2,
得6x=2.
方程两边同时除以6,
得x= .
小试牛刀
12.先阅读下面例题的解答过程,再解答后面的题目.
例:已知9-6y-4y2=7,求2y2+3y+7的值.
解:由9-6y-4y2=7,得-6y-4y2=7-9,
即6y+4y2=2,所以2y2+3y=1,所以2y2+3y+7=8.
题目:已知14a-5-21b2=9,求6b2-4a+5的值.
解:由14a-5-21b2=9,得14a-21b2=9+5,
即14a-21b2=14 . 所以3b2-2a=-2 .
所以6b2-4a+5=2(3b2-2a)+5=2×(-2)+5=1 .
小试牛刀
13.能不能从(a+3)x=b-1得到x= ,为什么?反过来,能不能从x= 得到(a+3)x=b-1,为什么?
解:不能从(a+3)x=b-1得到x= ,因为a+3有可能为0,而0不能作为除数;能从x=得到(a+3)x=b-1,因为当x= 时,a+3作为除数,说明a+3的值不为0,再根据等式的基本性质2,就能得到(a+3)x=b-1.
课堂小结
课堂小结
利用等式的基本性质变形的过程是由一个等式变形到另一个等式的过程,变形时应注意:
(1)等式两边都要参与运算,并且进行的是同一种运算;
(2)等式两边加减乘除的数或整式一定是同一个数或同一个整式;
(3)除以的数(或整式)不能为0.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
