冀教版(新)七上-5.3 解一元一次方程 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)七上-5.3 解一元一次方程 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
5.3 解一元一次方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们已经学习了等式的基本性质,怎样运用等式的这些性质去解一元一次方程呢?
新课精讲
探索新知
1
知识点
系数化为1
例1 解方程:(1)3x-2x=7; (2)5x=8+2 .
解:
( 1)3x-2x=7,
合并同类项,
得x=7 .
( 2)5x=8+2,
合并同类项,得5x=10,
系数化为1,得x=2.
解:
探索新知
总 结
解方程时未知数要化为1 .
典题精讲
1. 把方程- x=3的系数化为1的过程中,最恰当的叙述是( )
A.给方程两边同时乘-3
B.给方程两边同时除以
C.给方程两边同时乘
D.给方程两边同时除以3
C
典题精讲
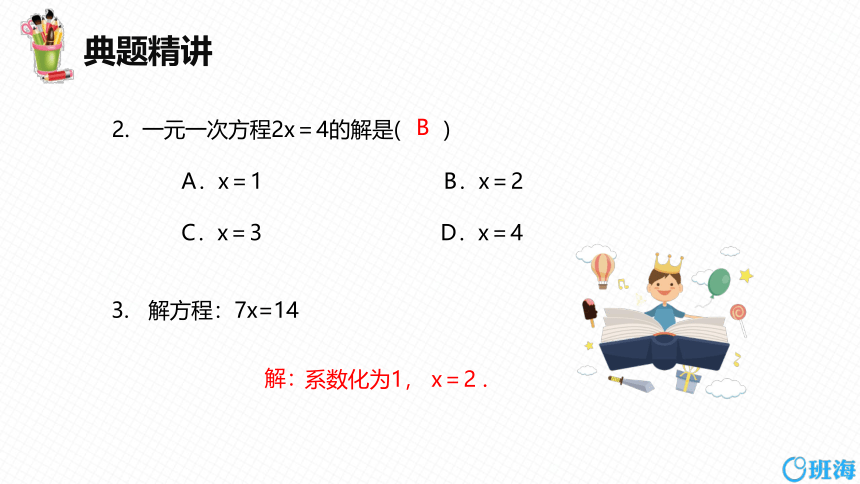
2. 一元一次方程2x=4的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
3. 解方程:7x=14
B
解:
系数化为1, x=2 .
探索新知
2
知识点
合并同类项
例2 解方程:(1)2x+3x=7+3; (2)3x+4x=14+7 .
解:
(1) 2x+3x=7+3
合并同类项,
得5x=10,
系数化为1,x=2;
(2) 3x+4x=14+7
合并同类项,
得7x=21,
系数化为1, x=3.
解:
探索新知
总 结
合并同类项时系数加减,字母和字母的指数不变 .
典题精讲
1. 下列各方程合并同类项不正确的是( )
A.由4x-2x=4,得2x=4
B.由2x-3x=3,得-x=3
C.由5x-2x+3x=12,得x=12
D.由-7x+2x=5,得-5x=5
C
典题精讲
2. 下列各方程合并同类项正确的是( )
A.由-3x+2x=1,得x=1
B.由x+2x+3x=9,得5x=9
C.由-x+2x-3x=5,得-4x=5
D.由 x+ x-x=2,得- x=2
D
探索新知
3
知识点
用合并同类项法解方程
例3 解方程:(1)2x-3x=1+5; (2) 2x-x=7+1 .
解:
(1)2x-3x=1+5 ,
合并同类项,得-x=6 ,
系数化为1,得x=-6.
(2)2x-x=7+1 ,
合并同类项,
得x=8 .
解:
探索新知
总 结
解方程时一般把含有未知数的合并,常数项合并 .
典题精讲
1 方程 +x+2x=210的解为( )
A.x=20 B.x=40 C.x=60 D.x=80
C
2 下面解方程的结果正确的是( )
A.方程4=3x-4x的解为x=4
B.方程 x= 的解为x=2
C.方程32=8x的解为x=
D.方程1-4= x的解为x=-9
D
学以致用
2.系数化为1是方程两边同时除以未知数的系数,使一元一次方程ax=
b(a≠0)变形为_______的形式,变形的依据是__________________.
1.合并同类项是将一元一次方程中含有未知数的项与常数项分别合并,使方程转化为ax=b(a≠0)的形式.解方程中的“合并同类项”这一变形的依据是_____________________.
3.解方程6x-3x+x=-16,
第一步:____________,得___________;
第二步:___________,得x=____ .
小试牛刀
乘法对加法的分配律
x=
等式的基本性质2
合并同类项
4x=-16
系数化为1
-4
小试牛刀
4.方程8x+6x-10x=8合并同类项正确的是( )
A.3x=8 B.4x=8 C.-4x=8 D.2x=8
B
5.下列解方程的过程中,错误的是( )
A.由-4x+5x=2,得x=-2
B.由y+2y=2,得3y=2,故y=
C.由-2x+x=4-2,得-x=2,故x=-2
D.由0.25a-0.75a=0,得-0.5a=0,故a=0
A
小试牛刀
6.对于任意四个有理数a,b,c,d,定义新运算: . 已知
=18,则x的值为( )
A.-1 B.2 C.3 D.4
7.关于x的方程3-x=2a与方程x+3x=28的解相同,则a的值为( )
A.2 B.-2
C.5 D.-5
B
C
小试牛刀
8.解方程:
(1)2x-4x+3x=5; (2) a+ a- a=-12 .
解:(1)合并同类项,得x=5.
解:(2)合并同类项,得 a=-12 .
系数化为1,得a=-18 .
小试牛刀
9.已知关于x的方程 x=3a-3的解为x=2,求(-a)2-2a+1的值 .
解:将x=2代入 +x=3a-3,
得3=3a-3,所以a=2.
当a=2时,(-a)2-2a+1=(-2)2-2×2+1=1.
小试牛刀
10.某中学的学生自己动手整修操场,如果让八年级学生单独工作,需要6 h完成;如果让九年级学生单独工作,需要4 h完成.现在由八、九年级学生一起工作,需多少小时才能完成任务?
解:设需x h才能完成任务.
由题意,得 x+ x=1,解得x= .
答:需 h才能完成任务.
小试牛刀
【思路点拨】列出已知条件:这群羊的2倍,加上这群羊的 ,再加上这群羊的 ,再加1等于100只羊.从实际问题中找到等量关系,建立模型:设这群羊有x只,列出方程求解,得答案.
11.我国明代数学家程大位曾提出一个有趣的问题.有一个人赶着一群羊
在前面走,另一个人牵着一只羊跟在后面,后面的人问赶羊的人说:
“你这群羊有一百只吗?”赶羊的人回答:“我再得这么一群羊,再得
这群羊的一半,再得这群羊的四分之一,把你牵的羊也给我,我恰好
有一百只羊.”问这群羊有多少只.
小试牛刀
解:设这群羊有x只.
由题意,得2x+ x+ x+1=100,
即 x+1=100,
解得x=36 .
答:这群羊有36只.
课堂小结
课堂小结
利用合并同类项法解方程的步骤:
它经历合并同类项,系数化为1这两步;合并同类项是化简、解方程的主要步骤,系数化为1,即在方程两边同时除以未知数的系数.
注意:系数为1或-1的项,合并时不能漏掉.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.3 解一元一次方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们已经学习了等式的基本性质,怎样运用等式的这些性质去解一元一次方程呢?
新课精讲
探索新知
1
知识点
系数化为1
例1 解方程:(1)3x-2x=7; (2)5x=8+2 .
解:
( 1)3x-2x=7,
合并同类项,
得x=7 .
( 2)5x=8+2,
合并同类项,得5x=10,
系数化为1,得x=2.
解:
探索新知
总 结
解方程时未知数要化为1 .
典题精讲
1. 把方程- x=3的系数化为1的过程中,最恰当的叙述是( )
A.给方程两边同时乘-3
B.给方程两边同时除以
C.给方程两边同时乘
D.给方程两边同时除以3
C
典题精讲
2. 一元一次方程2x=4的解是( )
A.x=1 B.x=2
C.x=3 D.x=4
3. 解方程:7x=14
B
解:
系数化为1, x=2 .
探索新知
2
知识点
合并同类项
例2 解方程:(1)2x+3x=7+3; (2)3x+4x=14+7 .
解:
(1) 2x+3x=7+3
合并同类项,
得5x=10,
系数化为1,x=2;
(2) 3x+4x=14+7
合并同类项,
得7x=21,
系数化为1, x=3.
解:
探索新知
总 结
合并同类项时系数加减,字母和字母的指数不变 .
典题精讲
1. 下列各方程合并同类项不正确的是( )
A.由4x-2x=4,得2x=4
B.由2x-3x=3,得-x=3
C.由5x-2x+3x=12,得x=12
D.由-7x+2x=5,得-5x=5
C
典题精讲
2. 下列各方程合并同类项正确的是( )
A.由-3x+2x=1,得x=1
B.由x+2x+3x=9,得5x=9
C.由-x+2x-3x=5,得-4x=5
D.由 x+ x-x=2,得- x=2
D
探索新知
3
知识点
用合并同类项法解方程
例3 解方程:(1)2x-3x=1+5; (2) 2x-x=7+1 .
解:
(1)2x-3x=1+5 ,
合并同类项,得-x=6 ,
系数化为1,得x=-6.
(2)2x-x=7+1 ,
合并同类项,
得x=8 .
解:
探索新知
总 结
解方程时一般把含有未知数的合并,常数项合并 .
典题精讲
1 方程 +x+2x=210的解为( )
A.x=20 B.x=40 C.x=60 D.x=80
C
2 下面解方程的结果正确的是( )
A.方程4=3x-4x的解为x=4
B.方程 x= 的解为x=2
C.方程32=8x的解为x=
D.方程1-4= x的解为x=-9
D
学以致用
2.系数化为1是方程两边同时除以未知数的系数,使一元一次方程ax=
b(a≠0)变形为_______的形式,变形的依据是__________________.
1.合并同类项是将一元一次方程中含有未知数的项与常数项分别合并,使方程转化为ax=b(a≠0)的形式.解方程中的“合并同类项”这一变形的依据是_____________________.
3.解方程6x-3x+x=-16,
第一步:____________,得___________;
第二步:___________,得x=____ .
小试牛刀
乘法对加法的分配律
x=
等式的基本性质2
合并同类项
4x=-16
系数化为1
-4
小试牛刀
4.方程8x+6x-10x=8合并同类项正确的是( )
A.3x=8 B.4x=8 C.-4x=8 D.2x=8
B
5.下列解方程的过程中,错误的是( )
A.由-4x+5x=2,得x=-2
B.由y+2y=2,得3y=2,故y=
C.由-2x+x=4-2,得-x=2,故x=-2
D.由0.25a-0.75a=0,得-0.5a=0,故a=0
A
小试牛刀
6.对于任意四个有理数a,b,c,d,定义新运算: . 已知
=18,则x的值为( )
A.-1 B.2 C.3 D.4
7.关于x的方程3-x=2a与方程x+3x=28的解相同,则a的值为( )
A.2 B.-2
C.5 D.-5
B
C
小试牛刀
8.解方程:
(1)2x-4x+3x=5; (2) a+ a- a=-12 .
解:(1)合并同类项,得x=5.
解:(2)合并同类项,得 a=-12 .
系数化为1,得a=-18 .
小试牛刀
9.已知关于x的方程 x=3a-3的解为x=2,求(-a)2-2a+1的值 .
解:将x=2代入 +x=3a-3,
得3=3a-3,所以a=2.
当a=2时,(-a)2-2a+1=(-2)2-2×2+1=1.
小试牛刀
10.某中学的学生自己动手整修操场,如果让八年级学生单独工作,需要6 h完成;如果让九年级学生单独工作,需要4 h完成.现在由八、九年级学生一起工作,需多少小时才能完成任务?
解:设需x h才能完成任务.
由题意,得 x+ x=1,解得x= .
答:需 h才能完成任务.
小试牛刀
【思路点拨】列出已知条件:这群羊的2倍,加上这群羊的 ,再加上这群羊的 ,再加1等于100只羊.从实际问题中找到等量关系,建立模型:设这群羊有x只,列出方程求解,得答案.
11.我国明代数学家程大位曾提出一个有趣的问题.有一个人赶着一群羊
在前面走,另一个人牵着一只羊跟在后面,后面的人问赶羊的人说:
“你这群羊有一百只吗?”赶羊的人回答:“我再得这么一群羊,再得
这群羊的一半,再得这群羊的四分之一,把你牵的羊也给我,我恰好
有一百只羊.”问这群羊有多少只.
小试牛刀
解:设这群羊有x只.
由题意,得2x+ x+ x+1=100,
即 x+1=100,
解得x=36 .
答:这群羊有36只.
课堂小结
课堂小结
利用合并同类项法解方程的步骤:
它经历合并同类项,系数化为1这两步;合并同类项是化简、解方程的主要步骤,系数化为1,即在方程两边同时除以未知数的系数.
注意:系数为1或-1的项,合并时不能漏掉.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
