冀教版(新)七上-5.4 一元一次方程的应用 第五课时【优质课件】
文档属性
| 名称 | 冀教版(新)七上-5.4 一元一次方程的应用 第五课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
第5课时
5.4 一元一次方程的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
若一种3年期国库券年利率为2.89%.如果要在3年后获得本息和10867元,现在应购买国库券多少元
解: 10867÷(1+2.89%×3)
=10867÷1.0867
=10000元
新课精讲
探索新知
1
知识点
积分问题
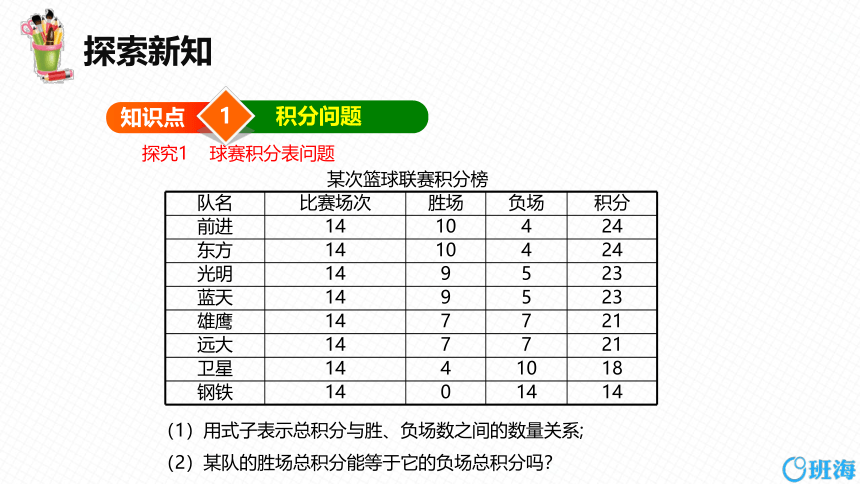
探究1 球赛积分表问题
某次篮球联赛积分榜
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)用式子表示总积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗?
探索新知
通过观察积分表,你能选择出其中哪一行最能说明负一场积几分吗?
分析:观察积分榜,从最下面一行数据可以看出:负一场积1分.设胜一场积x分,从表中其他任何一行可以列方程,求出x的值.例如,从第一行得方程10x+1×4 = 24.由此得x=2.用积分榜中其他行可以验证,得出结论:负一场积1分,胜一场积2分.
探索新知
(1)如果一个队胜m场,则负(14-m)场,胜场积分为2m,负场积分为 14 -m,总积分为2m+(14-m)=m+14.
(2)设一个队胜了 x场,则负了(14-x)场.如果这个队的胜场总积分 等于负场总积分,则得方程2x== 14 -x.由此得x=
探索新知
想一想:x表示什么量?它可以是分数吗?
由此你能得出什么结论?
解决实际问题时,要考虑得到的结果是不是符合实际.
x (所胜的场数)的值必须是整数,所以x=
不符合实际,由此可以判定没有哪个队的胜
场总积分等于负场总积分.
上面的问题说明,用方程解决实际问题时,
不仅要注意解方程的过程是否正确,还要检验
方程的解是否符合问题的实际意义.
这个问题说明:利用方程不仅能求具体数值,而且可以进行推理判断.
探索新知
这类问题中的基本关系有:
(1)比赛总场数=胜场数+负场数+平场数;
(2)比赛总积分=胜场积分+负场积分+平场积分.
探索新知
例1 为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
导引:设九年级一班胜x场,则负(8-x)场,根据得分情况直接列方程即可求解.
解: 设九年级一班胜x场,则负(8-x)场,
根据题意得2x+(8-x)=13.
解得x=5. 8-x=8-5=3. 答: 九年级一班胜5场,负3场.
探索新知
总 结
解决本题关键是找到比赛的总场数,先设出胜的场数,再表示出负的场数,根据总分数列方程求解.本题运用了方程思想.
探索新知
例2 某国进行足球赛共赛8轮(即每队均需参赛8场),胜一场得3分,平一场得1分,负一场得0分.在这次足球联赛中,猛虎队平的场数是负的场数的2倍,且8场比赛共得17分,该队共胜多少场?
解析:题中等量关系是:胜场积分+平场积分=17.
解:设该队负x场,则平的场数为2x场,胜的场数为
(8-x-2x)场,根据题意,得3(8-x-2x)+2x=17,
解这个方程得x=1.
∴8-x-2x=8-1-2=5. 答:该队共胜了5场.
探索新知
总 结
此类问题采用设间接未知数的方法,设某种场数为x,则其余两种场数都可以用含x的式子表示出来,从而可利用相等关系列方程.
探索新知
例3 某校高一年级有12个班.在学校组织的高一年级篮球比赛中,规定每两个班之间只进行一场比赛,每场比赛都要分出胜负,每班胜一场得2分,负一场得1分.某班要想在全部比赛中得18分,那么这个班的胜负场数应分别是多少?
解析:因为共有12个班,且规定每两个班之间只进行 一场比赛,所以这个班应该比赛11场,设胜了x场,则负了(11-x)场,根据得分为18分可列方程求解.
解: 设胜了x场,则负了(11-x)场.
依题意得2x+1·(11-x)=18, 解得x=7. ∴11-x=4.
答:这个班的胜负场数应分别是7和4.
探索新知
总 结
解本题关键是找到比赛的总场数,先设出胜的场数,再表示出负的场数,根据总分数列方程求解.本题运用了方程思想.
典题精讲
1.某校七年级11个班中开展篮球单循环比赛(每班需进行10场比赛).比赛规则:每场比赛都要分出胜负,胜一场得3分,负一场得-1分,已知七(2)班在所有的比赛中得到14分,若设该班胜x场,则x应满足的方程是( )
A.3x+(10-x)=14 B.3x-(10-x)=14
C.3x+x=14 D.3x-x=14
B
2.学校组织一次有关航天知识的竞赛,共有20道题,每道题答对得5分,答错或不答都倒扣1分,小明最终得76分,那么他答对了________道题.
16
探索新知
2
知识点
计费问题
探究2 电话计费问题
下表中有两种移动电话计费方式.
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
探索新知
考虑下列问题:
(1)设一个月内用移动电话主叫为tmin (t 是正整数). 根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
探索新知
分析: (1)由上表可知,计费与主叫时间相关,计费时首先要看主 叫是否 超过限定时间.因此,考虑t的取值时,两个主叫限定时间150 min和350 min 是不同时间范围的划分点.当t在不同时间范围内取值时,方式一和方式二的计费如下页表:
主叫时间t/min 方式一计费/元 方式二计费/元
t小于150 58 88
t=150 58 88
t大于150且小于350 58+0.25(t-150) 88
t=350 58+0.25(350-150)=108 88
t大于350 58+0.25(t-150) 88+0.19(t-350)
探索新知
(2)观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.下面比较不同时间范围内方式一和方式二的计费情况.
①当t小于或等于150时,按方式一的计费少.
②当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元.因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等.列方程58+0.25(t—150) = 88, 解得t=270.
因此,如果主叫时间恰是270 min,按两种方式的计费相等,都是88元; 如果主叫时间大于150 min且小于270 min,按方式一的计费少于按方式二的计费(88元);如果主叫时间大于270 min且小于350 min,按方式一的计费多于按方式二的计费(88元).
③当t=350时,按方式二的计费少.
探索新知
④当t大于350时,可以看出,按方式一的 计费为108元加上超过350 min部分的超时费 (0.25(t-350)),按方式二的计费为88元加上超 过350 min部分的超时费(0.19(t-350)),按方式二的计费少.
综合以上的分析,可以发现:
___________时,选择方案一省钱;
___________时,选择方案二省钱.
选一些具体数字,通过计算验证你的
发现是否正确.
当t大于350 时,按方式一的计费 58+0.25(t-150) 可变 形为 108 + 0.25(t - 350).对比按方式二 的计费,你能说明此 时按哪种方式的计费少吗?
t<270
t>270
探索新知
解答这类问题的一般步骤:
1.运用一元一次方程解应用题的方法,求解使方案值
相等的情况;
2.用特殊值试探去选择方案,取小于(或大于)一元一
次方程解的值,比较两种方案的优劣后下结论.
探索新知
例4 某市上网有两种收费方案,用户可任选其一:A为计时制——1元/时;B为包月制——80元/月,此外每种上网方式都附加通讯费0.1元/时.
(1)某用户每月上网40小时,选哪种方式比较合算?
(2)某用户每月有110元钱用于上网,选哪种方式比较合算?
(3)请你设计一个方案,使用户能合理地选择上网方式.
导引:(1)提供了上网时间40小时,根据“单价×总时长=总价”,求出A,B收费方案下的费用,进行比较;(2)提供了上网的总费用,已知上 网的单价,求出总时长进行比较;(3)根据用户的上网时长,比较哪种方案收费较少,帮其设计合理的方案.
探索新知
解:(1)如果用户每月上网40小时:
A计时制:40×(0.1+1)=44(元),
B包月制:80+40×0.1=84(元),
44<84,故选A计时制比较合算.
(2)设用户用110元上网,A计时制可上网x小时,B包月制可上网y小时,
则(1+0.1)x=110,解得x=100,
80+0.1 y=110,解得y =300.
因为100<300,故选B包月制比较合算.
探索新知
(3)设用户上网z小时,两种方式收费一样多.
则(1+0.1)z=80+0.1z.
解得z=80.
故上网不足80小时,选A计时制;
上网超过80小时,选B包月制;
上网恰好80小时,两种方案都一样.
探索新知
价目表 每月用水量 单价
不超出6 m3的部分 2元/m3
超出6 m3但不超出10 m3的部分 4元/m3
超出10 m3的部分 8元/m3
注:水费按月结算 例5 近几年我国部分地区不时出现的严重干旱,使我们认识 到节水的重要性.为了加强公民的节水意识,合理利用水资源,某市对自来水收费采用阶梯价格的调控手段以达到节水的目的.该市自来水收费价格见价目表.
探索新知
(1)若某户居民2月份用水10.5 m3,应交水费多少元?
(2)若该户居民3,4月份共用水16 m3(4月份用水量超过3月份),共交水费44元,则该户居民3,4月份各用水多少立方米?(结果精确到0.1 m3)
解:(1)由题意,得
2×6+4×(10-6)+8×(10.5-10)=32(元).
所以二月份应交水费32元.
探索新知
(2)设三月份用水x m3,则四月份用水(16-x) m3.
①当x≤6时,16-x≥10,
依题意,得2x+2×6+4×4+8(16-x-10)=44.
整理,得6x=32,所以x≈5.3,此时16-x≈10.7,符合题意.
②当6<x≤10时,6≤16-x<10,依题意,
得2×6+4×(x-6)+2×6+4(16-x-6)=44.
整理,得40=44,此方程无解.所以6<x≤10不可能成立.
③因为4月份用水量超过3月份,所以x不可能超过10.
综上所述,三月份用水约5.3 m3,四月份用水约10.7 m3.
典题精讲
1.参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
某人住院治疗后得到保险公司报销金额是1 100元,那么此人住院的医疗费是( )
A.1 000元 B.1 250元 C.1 500元 D.2 000元
住院医疗费 报销率(%)
不超过500元的部分 0
超过500~1 000元的部分 60
超过1 000~3 000元的部分 80
… …
D
典题精讲
2.张老师一家三口暑假准备参加旅游团去北京旅游,甲旅行社说:“如果父母买全票,小孩可半价优惠”;乙旅行社说:“全部按全票价的8折优惠”,若全票价为1 200元.则张老师应选择哪家旅行社?( )
A.选择甲 B.选择乙
C.选择甲、乙都一样 D.无法确定
B
3.某校准备为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.张老师经过计算,发现两家公司收费一样,则该校今年毕业生有________人.
500
学以致用
小试牛刀
1.在“地球停电一小时”活动的某地区烛光晚餐中,设座位有x排,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则下列方程正确的是 ( )
A.30x-8=31x+26 B.30x+8=31x+26
C.30x-8=31x-26 D.30x+8=31x-26
D
2.某种商品因换季准备打折出售,如果按定价的七五折出售将赔25元,而按定价的九折出售将赚20元.问这种商品的定价是多少?
设这种商品的定价为x元.根据题意,得0.75x+25=0.9x-20,
解得x=300. 答:这种商品的定价是300元.
解:
小试牛刀
3. A、B两地相距450千米,甲、乙两车分别从A、 B两地同时出发,相向而行,已知甲车的速度为120千米/时,乙车的速度为80千米/时,经过多少小时两车相距50千米?
两车相距50千米有两种情况,
情况一:两车未相遇,设经过x小时两车相距50千米,由题意,得(120+80)x+50=450 . 解得x=2.
情况二:两车相遇后继续前行,设经过y小时两车相距50千米,
由题意,得(120+80)y-50=450 . 解得y=2.5 .
答:经过2小时或2.5小时两车相距50千米.
解:
小试牛刀
4.某停车场的收费标准如下:中型汽车的停车费为12元/辆,小型汽车的停车费为8元/辆,现在停车场共有50辆中、小型汽车,这些车共需缴纳停车费480元,中、小型汽车各有多少辆?
设中型汽车有x辆,则小型汽车有(50-x)辆,
根据题意,得12x+8(50-x)=480,
解得x=20, 则50-x=50-20=30 .
答:中型汽车有20辆,小型汽车有30辆.
解:
小试牛刀
某小组8名同学参加一次知识竞赛,共答题10道,每题分值相同.每题答对得同样多的分,答错或不答扣同样多的分.情况如下:
学 号 答对题数 答错或不答题数 得分/分
1 8 2 70
2 9 1 85
3 9 1 85
4 5 5 25
5 7 3 55
6 10 0 100
7 4 6 10
8 8 2 70
5.
小试牛刀
设答对一道题得x分,
由6号同学的数据可得10x=100,解得x=10.
设答错或不答一题扣y分,
由1号同学的数据可得8×10-2y=70,解得y=5.
所以当答对的题数为n时,
得分为10n-5(10-n)=15n-50(分).
解:
(1) 如果答对的题数为n(0≤n≤10,且n为整数),用含n的式子表示得分;
小试牛刀
因为n为整数,所以不可能出现得零分的情况;
当答对题数为0,1,2或3时,得分为负分.
解:
(2)什么情况下,得分为零分,得分为负分?
小试牛刀
6. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间,房客多少人.
设该店有客房x间,则房客有(7x+7)人,
根据题意,得9(x-1)=7x+7,
解得x=8,则7x+7=7×8+7=63.
答:该店有客房8间,房客63人.
解:
小试牛刀
(2)假设店主李三公将客房进行改造后,房间数大大增加. 每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
若每间客房住4人,则63名房客至少需客房16间,
需付费20×16=320(钱),
若一次性订客房18间,则需付费20×18×0.8=288(钱)<320钱;
答:诗中“众客”再次一起入住,他们选择一次性订客房18间更合算.
解:
课堂小结
课堂小结
(1)谈谈本节课学到了哪些知识?学后有何感受?
(2)说说在积分问题中有哪些基本等量关系?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
第5课时
5.4 一元一次方程的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
若一种3年期国库券年利率为2.89%.如果要在3年后获得本息和10867元,现在应购买国库券多少元
解: 10867÷(1+2.89%×3)
=10867÷1.0867
=10000元
新课精讲
探索新知
1
知识点
积分问题
探究1 球赛积分表问题
某次篮球联赛积分榜
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)用式子表示总积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗?
探索新知
通过观察积分表,你能选择出其中哪一行最能说明负一场积几分吗?
分析:观察积分榜,从最下面一行数据可以看出:负一场积1分.设胜一场积x分,从表中其他任何一行可以列方程,求出x的值.例如,从第一行得方程10x+1×4 = 24.由此得x=2.用积分榜中其他行可以验证,得出结论:负一场积1分,胜一场积2分.
探索新知
(1)如果一个队胜m场,则负(14-m)场,胜场积分为2m,负场积分为 14 -m,总积分为2m+(14-m)=m+14.
(2)设一个队胜了 x场,则负了(14-x)场.如果这个队的胜场总积分 等于负场总积分,则得方程2x== 14 -x.由此得x=
探索新知
想一想:x表示什么量?它可以是分数吗?
由此你能得出什么结论?
解决实际问题时,要考虑得到的结果是不是符合实际.
x (所胜的场数)的值必须是整数,所以x=
不符合实际,由此可以判定没有哪个队的胜
场总积分等于负场总积分.
上面的问题说明,用方程解决实际问题时,
不仅要注意解方程的过程是否正确,还要检验
方程的解是否符合问题的实际意义.
这个问题说明:利用方程不仅能求具体数值,而且可以进行推理判断.
探索新知
这类问题中的基本关系有:
(1)比赛总场数=胜场数+负场数+平场数;
(2)比赛总积分=胜场积分+负场积分+平场积分.
探索新知
例1 为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
导引:设九年级一班胜x场,则负(8-x)场,根据得分情况直接列方程即可求解.
解: 设九年级一班胜x场,则负(8-x)场,
根据题意得2x+(8-x)=13.
解得x=5. 8-x=8-5=3. 答: 九年级一班胜5场,负3场.
探索新知
总 结
解决本题关键是找到比赛的总场数,先设出胜的场数,再表示出负的场数,根据总分数列方程求解.本题运用了方程思想.
探索新知
例2 某国进行足球赛共赛8轮(即每队均需参赛8场),胜一场得3分,平一场得1分,负一场得0分.在这次足球联赛中,猛虎队平的场数是负的场数的2倍,且8场比赛共得17分,该队共胜多少场?
解析:题中等量关系是:胜场积分+平场积分=17.
解:设该队负x场,则平的场数为2x场,胜的场数为
(8-x-2x)场,根据题意,得3(8-x-2x)+2x=17,
解这个方程得x=1.
∴8-x-2x=8-1-2=5. 答:该队共胜了5场.
探索新知
总 结
此类问题采用设间接未知数的方法,设某种场数为x,则其余两种场数都可以用含x的式子表示出来,从而可利用相等关系列方程.
探索新知
例3 某校高一年级有12个班.在学校组织的高一年级篮球比赛中,规定每两个班之间只进行一场比赛,每场比赛都要分出胜负,每班胜一场得2分,负一场得1分.某班要想在全部比赛中得18分,那么这个班的胜负场数应分别是多少?
解析:因为共有12个班,且规定每两个班之间只进行 一场比赛,所以这个班应该比赛11场,设胜了x场,则负了(11-x)场,根据得分为18分可列方程求解.
解: 设胜了x场,则负了(11-x)场.
依题意得2x+1·(11-x)=18, 解得x=7. ∴11-x=4.
答:这个班的胜负场数应分别是7和4.
探索新知
总 结
解本题关键是找到比赛的总场数,先设出胜的场数,再表示出负的场数,根据总分数列方程求解.本题运用了方程思想.
典题精讲
1.某校七年级11个班中开展篮球单循环比赛(每班需进行10场比赛).比赛规则:每场比赛都要分出胜负,胜一场得3分,负一场得-1分,已知七(2)班在所有的比赛中得到14分,若设该班胜x场,则x应满足的方程是( )
A.3x+(10-x)=14 B.3x-(10-x)=14
C.3x+x=14 D.3x-x=14
B
2.学校组织一次有关航天知识的竞赛,共有20道题,每道题答对得5分,答错或不答都倒扣1分,小明最终得76分,那么他答对了________道题.
16
探索新知
2
知识点
计费问题
探究2 电话计费问题
下表中有两种移动电话计费方式.
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
探索新知
考虑下列问题:
(1)设一个月内用移动电话主叫为tmin (t 是正整数). 根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
探索新知
分析: (1)由上表可知,计费与主叫时间相关,计费时首先要看主 叫是否 超过限定时间.因此,考虑t的取值时,两个主叫限定时间150 min和350 min 是不同时间范围的划分点.当t在不同时间范围内取值时,方式一和方式二的计费如下页表:
主叫时间t/min 方式一计费/元 方式二计费/元
t小于150 58 88
t=150 58 88
t大于150且小于350 58+0.25(t-150) 88
t=350 58+0.25(350-150)=108 88
t大于350 58+0.25(t-150) 88+0.19(t-350)
探索新知
(2)观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.下面比较不同时间范围内方式一和方式二的计费情况.
①当t小于或等于150时,按方式一的计费少.
②当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元.因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等.列方程58+0.25(t—150) = 88, 解得t=270.
因此,如果主叫时间恰是270 min,按两种方式的计费相等,都是88元; 如果主叫时间大于150 min且小于270 min,按方式一的计费少于按方式二的计费(88元);如果主叫时间大于270 min且小于350 min,按方式一的计费多于按方式二的计费(88元).
③当t=350时,按方式二的计费少.
探索新知
④当t大于350时,可以看出,按方式一的 计费为108元加上超过350 min部分的超时费 (0.25(t-350)),按方式二的计费为88元加上超 过350 min部分的超时费(0.19(t-350)),按方式二的计费少.
综合以上的分析,可以发现:
___________时,选择方案一省钱;
___________时,选择方案二省钱.
选一些具体数字,通过计算验证你的
发现是否正确.
当t大于350 时,按方式一的计费 58+0.25(t-150) 可变 形为 108 + 0.25(t - 350).对比按方式二 的计费,你能说明此 时按哪种方式的计费少吗?
t<270
t>270
探索新知
解答这类问题的一般步骤:
1.运用一元一次方程解应用题的方法,求解使方案值
相等的情况;
2.用特殊值试探去选择方案,取小于(或大于)一元一
次方程解的值,比较两种方案的优劣后下结论.
探索新知
例4 某市上网有两种收费方案,用户可任选其一:A为计时制——1元/时;B为包月制——80元/月,此外每种上网方式都附加通讯费0.1元/时.
(1)某用户每月上网40小时,选哪种方式比较合算?
(2)某用户每月有110元钱用于上网,选哪种方式比较合算?
(3)请你设计一个方案,使用户能合理地选择上网方式.
导引:(1)提供了上网时间40小时,根据“单价×总时长=总价”,求出A,B收费方案下的费用,进行比较;(2)提供了上网的总费用,已知上 网的单价,求出总时长进行比较;(3)根据用户的上网时长,比较哪种方案收费较少,帮其设计合理的方案.
探索新知
解:(1)如果用户每月上网40小时:
A计时制:40×(0.1+1)=44(元),
B包月制:80+40×0.1=84(元),
44<84,故选A计时制比较合算.
(2)设用户用110元上网,A计时制可上网x小时,B包月制可上网y小时,
则(1+0.1)x=110,解得x=100,
80+0.1 y=110,解得y =300.
因为100<300,故选B包月制比较合算.
探索新知
(3)设用户上网z小时,两种方式收费一样多.
则(1+0.1)z=80+0.1z.
解得z=80.
故上网不足80小时,选A计时制;
上网超过80小时,选B包月制;
上网恰好80小时,两种方案都一样.
探索新知
价目表 每月用水量 单价
不超出6 m3的部分 2元/m3
超出6 m3但不超出10 m3的部分 4元/m3
超出10 m3的部分 8元/m3
注:水费按月结算 例5 近几年我国部分地区不时出现的严重干旱,使我们认识 到节水的重要性.为了加强公民的节水意识,合理利用水资源,某市对自来水收费采用阶梯价格的调控手段以达到节水的目的.该市自来水收费价格见价目表.
探索新知
(1)若某户居民2月份用水10.5 m3,应交水费多少元?
(2)若该户居民3,4月份共用水16 m3(4月份用水量超过3月份),共交水费44元,则该户居民3,4月份各用水多少立方米?(结果精确到0.1 m3)
解:(1)由题意,得
2×6+4×(10-6)+8×(10.5-10)=32(元).
所以二月份应交水费32元.
探索新知
(2)设三月份用水x m3,则四月份用水(16-x) m3.
①当x≤6时,16-x≥10,
依题意,得2x+2×6+4×4+8(16-x-10)=44.
整理,得6x=32,所以x≈5.3,此时16-x≈10.7,符合题意.
②当6<x≤10时,6≤16-x<10,依题意,
得2×6+4×(x-6)+2×6+4(16-x-6)=44.
整理,得40=44,此方程无解.所以6<x≤10不可能成立.
③因为4月份用水量超过3月份,所以x不可能超过10.
综上所述,三月份用水约5.3 m3,四月份用水约10.7 m3.
典题精讲
1.参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
某人住院治疗后得到保险公司报销金额是1 100元,那么此人住院的医疗费是( )
A.1 000元 B.1 250元 C.1 500元 D.2 000元
住院医疗费 报销率(%)
不超过500元的部分 0
超过500~1 000元的部分 60
超过1 000~3 000元的部分 80
… …
D
典题精讲
2.张老师一家三口暑假准备参加旅游团去北京旅游,甲旅行社说:“如果父母买全票,小孩可半价优惠”;乙旅行社说:“全部按全票价的8折优惠”,若全票价为1 200元.则张老师应选择哪家旅行社?( )
A.选择甲 B.选择乙
C.选择甲、乙都一样 D.无法确定
B
3.某校准备为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.张老师经过计算,发现两家公司收费一样,则该校今年毕业生有________人.
500
学以致用
小试牛刀
1.在“地球停电一小时”活动的某地区烛光晚餐中,设座位有x排,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则下列方程正确的是 ( )
A.30x-8=31x+26 B.30x+8=31x+26
C.30x-8=31x-26 D.30x+8=31x-26
D
2.某种商品因换季准备打折出售,如果按定价的七五折出售将赔25元,而按定价的九折出售将赚20元.问这种商品的定价是多少?
设这种商品的定价为x元.根据题意,得0.75x+25=0.9x-20,
解得x=300. 答:这种商品的定价是300元.
解:
小试牛刀
3. A、B两地相距450千米,甲、乙两车分别从A、 B两地同时出发,相向而行,已知甲车的速度为120千米/时,乙车的速度为80千米/时,经过多少小时两车相距50千米?
两车相距50千米有两种情况,
情况一:两车未相遇,设经过x小时两车相距50千米,由题意,得(120+80)x+50=450 . 解得x=2.
情况二:两车相遇后继续前行,设经过y小时两车相距50千米,
由题意,得(120+80)y-50=450 . 解得y=2.5 .
答:经过2小时或2.5小时两车相距50千米.
解:
小试牛刀
4.某停车场的收费标准如下:中型汽车的停车费为12元/辆,小型汽车的停车费为8元/辆,现在停车场共有50辆中、小型汽车,这些车共需缴纳停车费480元,中、小型汽车各有多少辆?
设中型汽车有x辆,则小型汽车有(50-x)辆,
根据题意,得12x+8(50-x)=480,
解得x=20, 则50-x=50-20=30 .
答:中型汽车有20辆,小型汽车有30辆.
解:
小试牛刀
某小组8名同学参加一次知识竞赛,共答题10道,每题分值相同.每题答对得同样多的分,答错或不答扣同样多的分.情况如下:
学 号 答对题数 答错或不答题数 得分/分
1 8 2 70
2 9 1 85
3 9 1 85
4 5 5 25
5 7 3 55
6 10 0 100
7 4 6 10
8 8 2 70
5.
小试牛刀
设答对一道题得x分,
由6号同学的数据可得10x=100,解得x=10.
设答错或不答一题扣y分,
由1号同学的数据可得8×10-2y=70,解得y=5.
所以当答对的题数为n时,
得分为10n-5(10-n)=15n-50(分).
解:
(1) 如果答对的题数为n(0≤n≤10,且n为整数),用含n的式子表示得分;
小试牛刀
因为n为整数,所以不可能出现得零分的情况;
当答对题数为0,1,2或3时,得分为负分.
解:
(2)什么情况下,得分为零分,得分为负分?
小试牛刀
6. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间,房客多少人.
设该店有客房x间,则房客有(7x+7)人,
根据题意,得9(x-1)=7x+7,
解得x=8,则7x+7=7×8+7=63.
答:该店有客房8间,房客63人.
解:
小试牛刀
(2)假设店主李三公将客房进行改造后,房间数大大增加. 每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
若每间客房住4人,则63名房客至少需客房16间,
需付费20×16=320(钱),
若一次性订客房18间,则需付费20×18×0.8=288(钱)<320钱;
答:诗中“众客”再次一起入住,他们选择一次性订客房18间更合算.
解:
课堂小结
课堂小结
(1)谈谈本节课学到了哪些知识?学后有何感受?
(2)说说在积分问题中有哪些基本等量关系?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
