冀教版(新)七上-5.4 一元一次方程的应用 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)七上-5.4 一元一次方程的应用 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
第1课时
5.4 一元一次方程的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
旧知回顾
新课精讲
探索新知
1
知识点
列一元一次方程解实际问题的步骤
列方程解应用题的一般步骤:
设未知数、列方程、解方程、检验所得结果、确定答案;可简要地概括为“设、列、解、检、答”.
探索新知
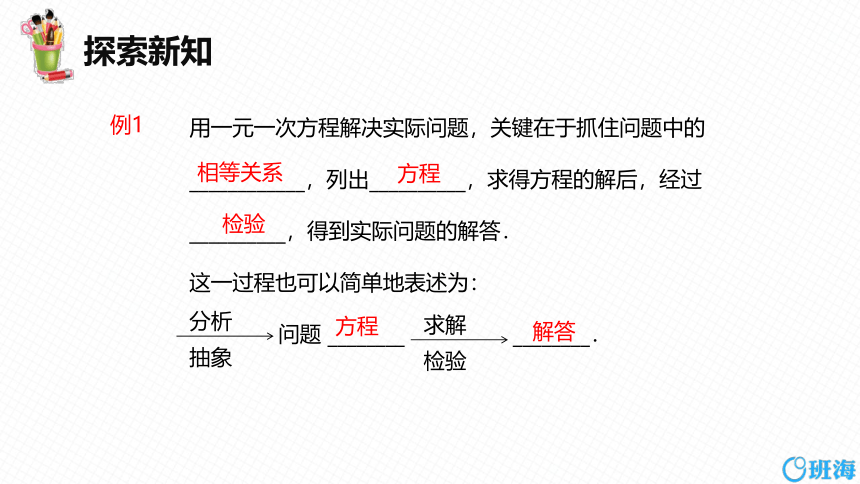
用一元一次方程解决实际问题,关键在于抓住问题中的____________,列出__________,求得方程的解后,经过__________,得到实际问题的解答.
这一过程也可以简单地表述为:
问题 ________ ________.
例1
分析
抽象
求解
检验
相等关系
方程
检验
方程
解答
探索新知
3月12日是植树节,七年级170名学生参加义务植树活动,如果平均一名男生一天能挖树坑3个,平均一名女生一天能种树7棵,要正好使每个树坑种一棵树,则该年级的男生、女生各有多少人?
(1)审题:审清题意,找出已知量和未知量;
(2)设未知数:设该年级的男生有x人,那么女生有__________人;
(3)列方程:根据相等关系,列方程为_______________;
(4)解方程,得x=________,则女生有______人;
(5)检验:将解得的未知数的值放入实际问题中进行验证;
(6)作答:答:该年级有男生______人,女生______人.
(170-x)
3x=7(170-x)
119
51
119
51
例2
探索新知
2
知识点
设未知数的方法
设未知数的方法:
(1)直接设未知数:即题目求什么就设什么为未知数;
(2)间接设未知数:直接设所求的量为未知数,不便列方程时,可设与所求量有关系的量作为未知数,进而求出所求的量.
探索新知
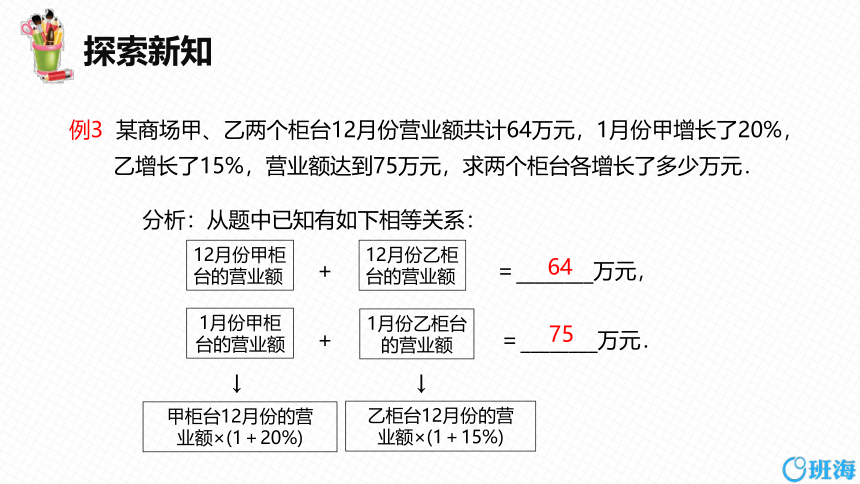
例3 某商场甲、乙两个柜台12月份营业额共计64万元,1月份甲增长了20%,
乙增长了15%,营业额达到75万元,求两个柜台各增长了多少万元.
分析:从题中已知有如下相等关系:
+ =________万元,
+ =________万元.
↓ ↓
12月份甲柜
台的营业额
12月份乙柜
台的营业额
1月份甲柜台的营业额
1月份乙柜台
的营业额
甲柜台12月份的营
业额×(1+20%)
乙柜台12月份的营
业额×(1+15%)
64
75
探索新知
解:方法1:设1月份甲柜台的营业额增长了x万元,则1月份乙柜台
的营业额增长了_______________万元,依题意,列方程可得
解之得x=________.
75-64-x=____________________=________.
方法2:设12月份甲柜台的营业额是y万元,则
乙柜台的营业额是(64-y)万元.
(75-64-x)
75-64-x
5.6
75-64-5.6
5.4
探索新知
依据题意,列方程得________________________________________,
解得y=________.
所以甲柜台增长了______×20%=______(万元),
乙柜台增长了__________×15%=________(万元).
答:甲柜台的营业额增长了________万元,乙柜台
的营业额增长了________万元.
(1+20%)y+(1+15%)(64-y)=75
28
28
5.6
(64-28)
5.4
5.6
5.4
探索新知
3
知识点
一元一次方程解法的应用
例4 联华商场以150元/台的价格购进某款电风扇若干台,很快售完.商场用相同的货款再次购进这款电风扇,因价格提高30元,进货量减少了10台.
(1)这两次各购进电风扇多少台?
(2)商场以250元/台的售价卖完这两批电风扇,商场获利多少元?
探索新知
解:(1)设第一次购进电风扇x台,
则第二次购进电风扇(x-10)台.
由题意可得150x=180(x-10),解得x=60.
则x-10=60-10=50.
所以第一次购进电风扇60台,第二次购进电风扇50台.
(2)商场获利为
(250-150)×60+(250-180)×50=9 500(元).
所以商场以250元/台的售价卖完这两批电风扇,
商场获利9 500元.
探索新知
解:设A型、B型、C型这三种洗衣机分别计划生产x台、2x台、14x台.
由题意得x+2x+14x=25 500.解得x=1 500.
所以2x=2×1 500=3 000,
14x=14×1 500=21 000.
答:这三种洗衣机分别计划生产1 500台、3 000台、21 000台.
例5 洗衣机厂今年计划生产洗衣机25 500台,其中A型,B型,C
型三种洗衣机的产量之比为1∶2∶14,这三种洗衣机分别计
划生产多少台?
探索新知
例6 现有菜地975公顷,要种植白菜、西红柿和芹菜,其中种白菜
与种西红柿的面积比是3∶2,种西红柿与种芹菜的面积比是
5∶7,则三种蔬菜各种多少公顷?
解:因为3∶2=15∶10,5∶7=10∶14,所以白菜、西红柿、芹菜的种植面积之比为
15∶10∶14.
设白菜的种植面积为15x公顷,则西红柿的种植
面积为10x公顷,芹菜的种植面积为14x公顷.
根据题意,得15x+10x+14x=975,解得x=25.
则15x=375,10x=250,14x=350.
答:种白菜的面积为375公顷,种西红柿的面积为250公顷,种芹菜的面积为350公顷.
探索新知
例7 甲种货车和乙种货车的装载量及每辆车的运费如下表所示,现有
货物130 t,要求一次装完,并且每辆要满载,探究怎样安排运
费最省?需多少元?
甲 乙
每辆车装载量 30 t 20 t
每辆车的运费 500元 400元
探索新知
解:设甲种货车为x辆,则乙种货车为
且x是自然数,
当x=1时,
运费为1×500+5×400=2 500(元);
当x=3时,
运费为3×500+2×400=2 300(元)<2 500(元).
故安排3辆甲种货车和2辆乙种货车,运费最省,需2 300元.
也是自然数.
探索新知
此题关键是审清表格,利用车辆数为自然数这
一特殊情况进行尝试,直到符合条件为止,将所有
的可能都列举出来,进行比较.
归 纳
探索新知
例8 某景点的门票价格如下表:
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少
于50人,(2)班人数多于50人且少于100人,如果两班都以班
为单位单独购票,则一共支付1 118元;如果两班联合起来作
为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
购票人数/人 1~50 51~100 100以上
每人门票价/元 12 10 8
探索新知
解: (1)设七年级(1)班有x人,
则七年级(2)班有
由题意,得
解得x=49.
则
答:七年级(1)班有49人,七年级(2)班有53人.
探索新知
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
解:七年级(1)班:(12-8)×49=196(元);
七年级(2)班:(12-10)×53=106(元).
答:七年级(1)班节约了196元,
七年级(2)班节约了106元.
学以致用
小试牛刀
将方程 的两边同时乘以_________可得到3(x+2)=2(2x+3),这种变形叫_________,其依据是__________________.
1.
12
去分母
等式的性质2
再解方程 的过程中,①去分母,得6-10x-1=2(2x+1);去括号,得6-10x+1=4x+2;③移项,得-10x-4x=2-6-1;④合并同类型,得-14x=-5;⑤系数化为1,得x= .其中开始出现错误步骤是_____________.(填序号)
2.
①
小试牛刀
下面是解方程 的过程,请在前面的括号内填写变形
步骤,在后面的括号内填写变形依据.
解:原方程棵变形为 ,( )
去分母,得3(3x+5)=2(2x-1). ( )
去括号,得9x+15=4x-2.( )
( ),得9x-4x=-15-2;( )
( ),得5x=17;
( ),得x= ( )
3.
分数的基本性质
等式的性质2
去括号法则
移项
等式的性质1
合并同类型
系数化为1
等式的性质2
小试牛刀
4.
利用等式的性质解方程 的结果是( )
A.x=2 B.x=-2
C.x=4 D.x=-4
A
5.
解方程 . 下面几种解法中,简便得是( )
A.先两边同乘6 B.先两边同乘5.
C.先去括号再移项 D. 括号内先通分
C
小试牛刀
6.解方程.
(1)
小试牛刀
(2)
6.解方程.
课堂小结
课堂小结
设未知数,列方程
用一元一次方程解决实际问题的基本过程如下:
实际问题
一元一次方程
实际问题
的答案
一元一次方程的解(x=a)
解
方
程
检 验
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
第1课时
5.4 一元一次方程的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
旧知回顾
新课精讲
探索新知
1
知识点
列一元一次方程解实际问题的步骤
列方程解应用题的一般步骤:
设未知数、列方程、解方程、检验所得结果、确定答案;可简要地概括为“设、列、解、检、答”.
探索新知
用一元一次方程解决实际问题,关键在于抓住问题中的____________,列出__________,求得方程的解后,经过__________,得到实际问题的解答.
这一过程也可以简单地表述为:
问题 ________ ________.
例1
分析
抽象
求解
检验
相等关系
方程
检验
方程
解答
探索新知
3月12日是植树节,七年级170名学生参加义务植树活动,如果平均一名男生一天能挖树坑3个,平均一名女生一天能种树7棵,要正好使每个树坑种一棵树,则该年级的男生、女生各有多少人?
(1)审题:审清题意,找出已知量和未知量;
(2)设未知数:设该年级的男生有x人,那么女生有__________人;
(3)列方程:根据相等关系,列方程为_______________;
(4)解方程,得x=________,则女生有______人;
(5)检验:将解得的未知数的值放入实际问题中进行验证;
(6)作答:答:该年级有男生______人,女生______人.
(170-x)
3x=7(170-x)
119
51
119
51
例2
探索新知
2
知识点
设未知数的方法
设未知数的方法:
(1)直接设未知数:即题目求什么就设什么为未知数;
(2)间接设未知数:直接设所求的量为未知数,不便列方程时,可设与所求量有关系的量作为未知数,进而求出所求的量.
探索新知
例3 某商场甲、乙两个柜台12月份营业额共计64万元,1月份甲增长了20%,
乙增长了15%,营业额达到75万元,求两个柜台各增长了多少万元.
分析:从题中已知有如下相等关系:
+ =________万元,
+ =________万元.
↓ ↓
12月份甲柜
台的营业额
12月份乙柜
台的营业额
1月份甲柜台的营业额
1月份乙柜台
的营业额
甲柜台12月份的营
业额×(1+20%)
乙柜台12月份的营
业额×(1+15%)
64
75
探索新知
解:方法1:设1月份甲柜台的营业额增长了x万元,则1月份乙柜台
的营业额增长了_______________万元,依题意,列方程可得
解之得x=________.
75-64-x=____________________=________.
方法2:设12月份甲柜台的营业额是y万元,则
乙柜台的营业额是(64-y)万元.
(75-64-x)
75-64-x
5.6
75-64-5.6
5.4
探索新知
依据题意,列方程得________________________________________,
解得y=________.
所以甲柜台增长了______×20%=______(万元),
乙柜台增长了__________×15%=________(万元).
答:甲柜台的营业额增长了________万元,乙柜台
的营业额增长了________万元.
(1+20%)y+(1+15%)(64-y)=75
28
28
5.6
(64-28)
5.4
5.6
5.4
探索新知
3
知识点
一元一次方程解法的应用
例4 联华商场以150元/台的价格购进某款电风扇若干台,很快售完.商场用相同的货款再次购进这款电风扇,因价格提高30元,进货量减少了10台.
(1)这两次各购进电风扇多少台?
(2)商场以250元/台的售价卖完这两批电风扇,商场获利多少元?
探索新知
解:(1)设第一次购进电风扇x台,
则第二次购进电风扇(x-10)台.
由题意可得150x=180(x-10),解得x=60.
则x-10=60-10=50.
所以第一次购进电风扇60台,第二次购进电风扇50台.
(2)商场获利为
(250-150)×60+(250-180)×50=9 500(元).
所以商场以250元/台的售价卖完这两批电风扇,
商场获利9 500元.
探索新知
解:设A型、B型、C型这三种洗衣机分别计划生产x台、2x台、14x台.
由题意得x+2x+14x=25 500.解得x=1 500.
所以2x=2×1 500=3 000,
14x=14×1 500=21 000.
答:这三种洗衣机分别计划生产1 500台、3 000台、21 000台.
例5 洗衣机厂今年计划生产洗衣机25 500台,其中A型,B型,C
型三种洗衣机的产量之比为1∶2∶14,这三种洗衣机分别计
划生产多少台?
探索新知
例6 现有菜地975公顷,要种植白菜、西红柿和芹菜,其中种白菜
与种西红柿的面积比是3∶2,种西红柿与种芹菜的面积比是
5∶7,则三种蔬菜各种多少公顷?
解:因为3∶2=15∶10,5∶7=10∶14,所以白菜、西红柿、芹菜的种植面积之比为
15∶10∶14.
设白菜的种植面积为15x公顷,则西红柿的种植
面积为10x公顷,芹菜的种植面积为14x公顷.
根据题意,得15x+10x+14x=975,解得x=25.
则15x=375,10x=250,14x=350.
答:种白菜的面积为375公顷,种西红柿的面积为250公顷,种芹菜的面积为350公顷.
探索新知
例7 甲种货车和乙种货车的装载量及每辆车的运费如下表所示,现有
货物130 t,要求一次装完,并且每辆要满载,探究怎样安排运
费最省?需多少元?
甲 乙
每辆车装载量 30 t 20 t
每辆车的运费 500元 400元
探索新知
解:设甲种货车为x辆,则乙种货车为
且x是自然数,
当x=1时,
运费为1×500+5×400=2 500(元);
当x=3时,
运费为3×500+2×400=2 300(元)<2 500(元).
故安排3辆甲种货车和2辆乙种货车,运费最省,需2 300元.
也是自然数.
探索新知
此题关键是审清表格,利用车辆数为自然数这
一特殊情况进行尝试,直到符合条件为止,将所有
的可能都列举出来,进行比较.
归 纳
探索新知
例8 某景点的门票价格如下表:
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少
于50人,(2)班人数多于50人且少于100人,如果两班都以班
为单位单独购票,则一共支付1 118元;如果两班联合起来作
为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
购票人数/人 1~50 51~100 100以上
每人门票价/元 12 10 8
探索新知
解: (1)设七年级(1)班有x人,
则七年级(2)班有
由题意,得
解得x=49.
则
答:七年级(1)班有49人,七年级(2)班有53人.
探索新知
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
解:七年级(1)班:(12-8)×49=196(元);
七年级(2)班:(12-10)×53=106(元).
答:七年级(1)班节约了196元,
七年级(2)班节约了106元.
学以致用
小试牛刀
将方程 的两边同时乘以_________可得到3(x+2)=2(2x+3),这种变形叫_________,其依据是__________________.
1.
12
去分母
等式的性质2
再解方程 的过程中,①去分母,得6-10x-1=2(2x+1);去括号,得6-10x+1=4x+2;③移项,得-10x-4x=2-6-1;④合并同类型,得-14x=-5;⑤系数化为1,得x= .其中开始出现错误步骤是_____________.(填序号)
2.
①
小试牛刀
下面是解方程 的过程,请在前面的括号内填写变形
步骤,在后面的括号内填写变形依据.
解:原方程棵变形为 ,( )
去分母,得3(3x+5)=2(2x-1). ( )
去括号,得9x+15=4x-2.( )
( ),得9x-4x=-15-2;( )
( ),得5x=17;
( ),得x= ( )
3.
分数的基本性质
等式的性质2
去括号法则
移项
等式的性质1
合并同类型
系数化为1
等式的性质2
小试牛刀
4.
利用等式的性质解方程 的结果是( )
A.x=2 B.x=-2
C.x=4 D.x=-4
A
5.
解方程 . 下面几种解法中,简便得是( )
A.先两边同乘6 B.先两边同乘5.
C.先去括号再移项 D. 括号内先通分
C
小试牛刀
6.解方程.
(1)
小试牛刀
(2)
6.解方程.
课堂小结
课堂小结
设未知数,列方程
用一元一次方程解决实际问题的基本过程如下:
实际问题
一元一次方程
实际问题
的答案
一元一次方程的解(x=a)
解
方
程
检 验
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
