冀教版(新)七上-2.8 平面图形的旋转【优质教案】
文档属性
| 名称 | 冀教版(新)七上-2.8 平面图形的旋转【优质教案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 317.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览


文档简介
班海数学精批——一本可精细批改的教辅
2.8 平面图形的旋转
学习目标:
1.理解旋转的有关概念,能按要求作出简单平面图形旋转后的图形;(重点、难点)
2.理解并掌握图形旋转的性质及其应用.(重点、难点)
学习重点:掌握旋转的有关概念.
学习难点:掌握图形旋转的性质及其应用.
1、知识链接
1.几何研究的主要内容是图形的_______、_________和___________;
几何图形分________和___________.
2.我们身边有许多平面图形,试举例说明.
___________、__________、___________、___________、____________.
3.角的定义
角可以看做一条射线绕着端点_____到另一位置所形成的图形.
2、新知预习
观察与思考
1.旋转的有关概念
观察下列图片:
(1)时钟上的秒针在不停的转动; (2)大风车的转动;(3)飞速转动的电风扇叶片;(4)汽车上的括水器;(5)由平面图形转动而产生的奇妙图案.
想一想,这些情景中的转动现象,有什么共同特征
··○○○
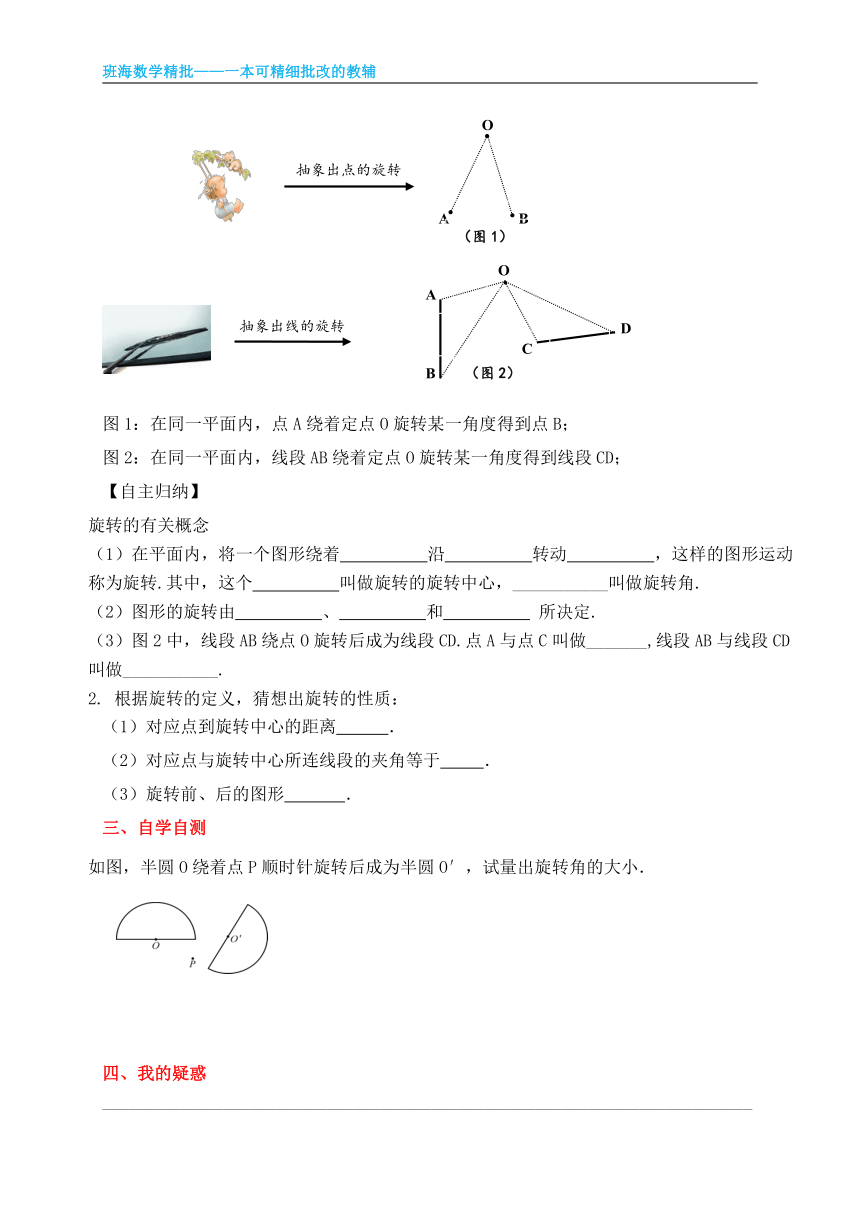
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B;
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD;
【自主归纳】
旋转的有关概念
(1)在平面内,将一个图形绕着 沿 转动 ,这样的图形运动称为旋转.其中,这个 叫做旋转的旋转中心,___________叫做旋转角.
(2)图形的旋转由 、 和 所决定.
(3)图2中,线段AB绕点O旋转后成为线段CD.点A与点C叫做_______,线段AB与线段CD叫做___________.
2. 根据旋转的定义,猜想出旋转的性质:
(1)对应点到旋转中心的距离 .
(2)对应点与旋转中心所连线段的夹角等于 .
(3)旋转前、后的图形 .
三、自学自测
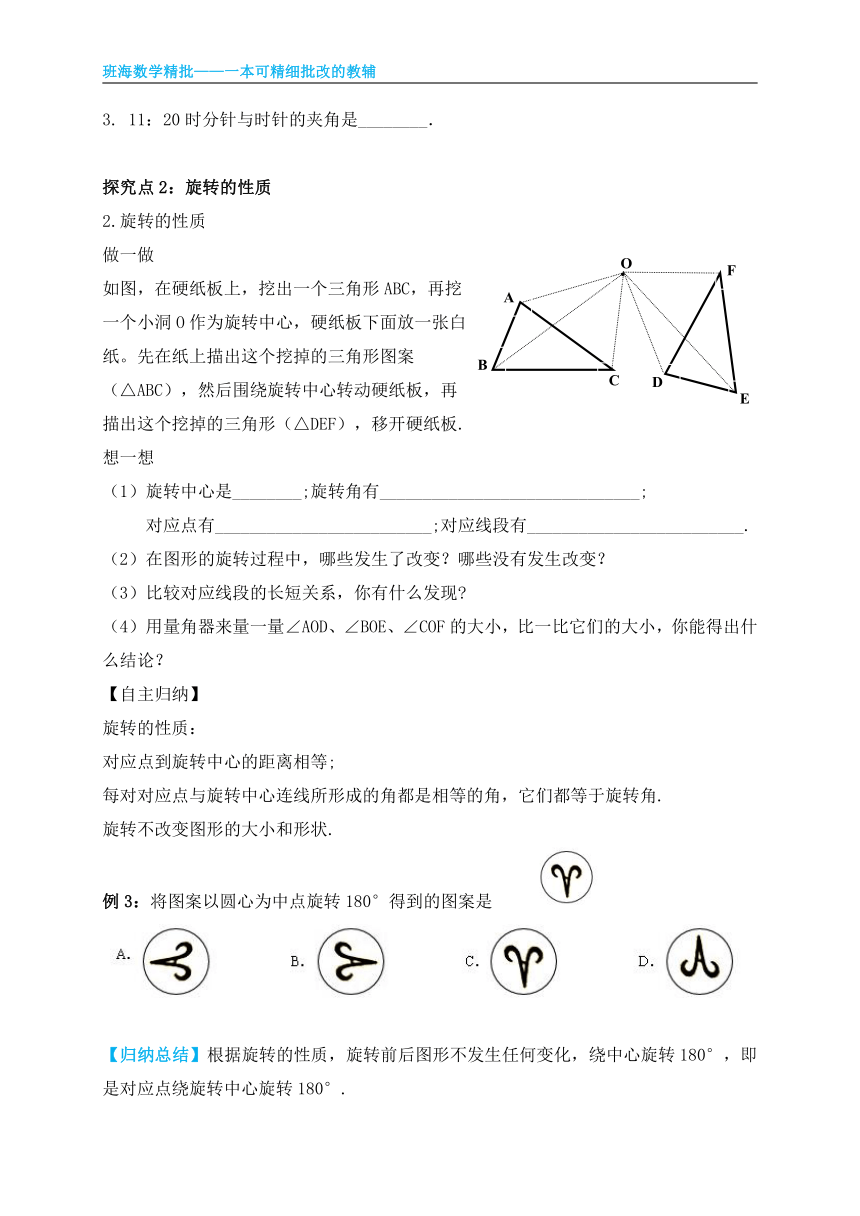
如图,半圆O绕着点P顺时针旋转后成为半圆O′,试量出旋转角的大小.
四、我的疑惑
_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
_____________________________________________________________________________ _____________________________________________________________________________
1、
2、要点探究
探究点1:生活中的旋转现象
例1:下列生活实践中,不是旋转的是( )
A.传送带传送货物 B.螺旋桨的运动 C.风车风轮的运动 D.自行车车轮的运动
【归纳总结】正确理解旋转的定义是关键,旋转就是将图形绕某点旋转一定的角度,旋转后所得图形与原图形的形状、大小一样.
例2:时钟在下午4点到5点之间,什么时刻分针和时针能够构成45°角.
【归纳总结】钟表上分针每分钟转过6°的角,每小时转过360°角,时针每分钟转过0.5°的角,每小时转过30°的角,钟表上一大格为30°.
【针对训练】
1.下列现象中,属于旋转的是( )
A.摩托车在急刹车时向前滑动 B.拧开水龙头
C.雪橇在雪地里滑动 D.电梯的上升与下降
2.时钟钟面上的秒针绕中心旋转180°,则下列说法正确的是( )
A.时针不动,分针旋转了6° B.时针不动,分针旋转了3°
C.时针和分针都没有旋转 D.分针旋转3°,时针旋转角度很小
3. 11:20时分针与时针的夹角是________.
探究点2:旋转的性质
2.旋转的性质
做一做
如图,在硬纸板上,挖出一个三角形ABC,再挖
一个小洞O作为旋转中心,硬纸板下面放一张白
纸。先在纸上描出这个挖掉的三角形图案
(△ABC),然后围绕旋转中心转动硬纸板,再
描出这个挖掉的三角形(△DEF),移开硬纸板.
想一想
(1)旋转中心是________;旋转角有______________________________;
对应点有_________________________;对应线段有_________________________.
(2)在图形的旋转过程中,哪些发生了改变?哪些没有发生改变?
(3)比较对应线段的长短关系,你有什么发现
(4)用量角器来量一量∠AOD、∠BOE、∠COF的大小,比一比它们的大小,你能得出什么结论?
【自主归纳】
旋转的性质:
对应点到旋转中心的距离相等;
每对对应点与旋转中心连线所形成的角都是相等的角,它们都等于旋转角.
旋转不改变图形的大小和形状.
例3:将图案以圆心为中点旋转180°得到的图案是
【归纳总结】根据旋转的性质,旋转前后图形不发生任何变化,绕中心旋转180°,即是对应点绕旋转中心旋转180°.
例4:如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B、A、C’在同一条直线上,则三角板ABC的旋转角度为( )
【针对训练】
1.将数字“6”旋转180°后得到数字“9”,将数字“9”旋转180°后得到数字“6”,现将数字“69”旋转180°后,得到的数字是_________.
探究点3:作图——旋转变换
例5:将△ABC放在每个小正方形为1的网格中,点B、C落在格点上,P是△ABC内部一点,(1)将△ABC绕点A逆时针旋转90°,画出旋转后的图形;
(2)将△APC绕点C顺时针旋转60°,画出旋转后的图形.
(保留作图痕迹)
【归纳总结】旋转作图的步骤:(1)确定旋转中心、旋转方向及旋转角的大小;
(2)确定已知图形的关键点(比如线段的两个端点、三角形的三个顶点等);
(3)确定各关键点的对应点.(将图形的各关键点与旋转中心连接,按规定方向旋转规定角度,找到该点的对应点);(4)按原图顶点的顺序连接各对应点,即得旋转后的图形.
【针对训练】
二、课堂小结
内容
旋转的有关定义 在平面内,将一个图形绕着 沿 转动 , 这样的图形运动称为旋转.其中,这个 叫做旋转的旋转中心,_ _________叫做旋转角.
旋转的性质 对应点到_________的距离相等;每对对应点与旋转中心连线所形成的角都是________的角,它们都等于__________. 旋转不改变图形的________和__________.
1.以下现象中属于旋转的有( )个.
(1)荡秋千 ;(2)火车行驶;(3)方向盘的移动;(4)钟表的摆动;(5)圆规画圆.
A.1 B.2 C.3 D.4
2.时钟上的分针匀速旋转一周需要60min,则经过20min,分针旋转了( )
A.20° B.60° C.90° D.120°
6.学校早上8时开始上课,45分钟后开始下课,这节课分针转动的角度为________.
7.将一个自然数旋转180°后,可以发现一个有趣的现象,有的自然数旋转后还是自然数.例如,808,旋转180°后仍是808,.又如169旋转180°后是691.而有的旋转180°后就不是自然数了,如37.试写出一个旋转180°后仍等于本身的五位数:_______(数字不能完全相同).
8.如图所示,画出三角形ABC绕点C逆时针旋转90°后的图形.(画在图上)
当堂检测参考答案:
1.C 2.D 3.B 4.A
5.17°
6.270°
7.80108
8.如图所示:
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
自主学习
抽象出点的旋转
A
B
(图1)
O
抽象出线的旋转
·
O
A
B
C
D
(图2)
合作探究
·
O
A
B
C
F
D
E
【归纳总结】 本题考查的是旋转的性质,掌握对应点与旋转中心的连线所形成的角等于旋转角是解题的关键.
A.60° B.90° C.120° D.150°
2.如图,将直角三角形ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于__________.
请在途中画出线段AB以O为旋转中心逆时针分别旋转90°,180°,270° 时对应的图形.
当堂检测
3.
4.如图,在直角三角形ABC中,∠BAC=90°,将直角三角形ABC绕点C按逆时针方向旋转48°得到直角三角形A’B’C’,点A在边B’C上,则∠B’的大小为( )
A.42° B.48° C.52° D.58°
5.如图所示,△ABC中,∠BAC=33°,将△ABC绕点A顺时针方向旋转50°,对应得到△AB’C’,则∠B’AC的度数为:___________ .
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.8 平面图形的旋转
学习目标:
1.理解旋转的有关概念,能按要求作出简单平面图形旋转后的图形;(重点、难点)
2.理解并掌握图形旋转的性质及其应用.(重点、难点)
学习重点:掌握旋转的有关概念.
学习难点:掌握图形旋转的性质及其应用.
1、知识链接
1.几何研究的主要内容是图形的_______、_________和___________;
几何图形分________和___________.
2.我们身边有许多平面图形,试举例说明.
___________、__________、___________、___________、____________.
3.角的定义
角可以看做一条射线绕着端点_____到另一位置所形成的图形.
2、新知预习
观察与思考
1.旋转的有关概念
观察下列图片:
(1)时钟上的秒针在不停的转动; (2)大风车的转动;(3)飞速转动的电风扇叶片;(4)汽车上的括水器;(5)由平面图形转动而产生的奇妙图案.
想一想,这些情景中的转动现象,有什么共同特征
··○○○
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B;
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD;
【自主归纳】
旋转的有关概念
(1)在平面内,将一个图形绕着 沿 转动 ,这样的图形运动称为旋转.其中,这个 叫做旋转的旋转中心,___________叫做旋转角.
(2)图形的旋转由 、 和 所决定.
(3)图2中,线段AB绕点O旋转后成为线段CD.点A与点C叫做_______,线段AB与线段CD叫做___________.
2. 根据旋转的定义,猜想出旋转的性质:
(1)对应点到旋转中心的距离 .
(2)对应点与旋转中心所连线段的夹角等于 .
(3)旋转前、后的图形 .
三、自学自测
如图,半圆O绕着点P顺时针旋转后成为半圆O′,试量出旋转角的大小.
四、我的疑惑
_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
_____________________________________________________________________________ _____________________________________________________________________________
1、
2、要点探究
探究点1:生活中的旋转现象
例1:下列生活实践中,不是旋转的是( )
A.传送带传送货物 B.螺旋桨的运动 C.风车风轮的运动 D.自行车车轮的运动
【归纳总结】正确理解旋转的定义是关键,旋转就是将图形绕某点旋转一定的角度,旋转后所得图形与原图形的形状、大小一样.
例2:时钟在下午4点到5点之间,什么时刻分针和时针能够构成45°角.
【归纳总结】钟表上分针每分钟转过6°的角,每小时转过360°角,时针每分钟转过0.5°的角,每小时转过30°的角,钟表上一大格为30°.
【针对训练】
1.下列现象中,属于旋转的是( )
A.摩托车在急刹车时向前滑动 B.拧开水龙头
C.雪橇在雪地里滑动 D.电梯的上升与下降
2.时钟钟面上的秒针绕中心旋转180°,则下列说法正确的是( )
A.时针不动,分针旋转了6° B.时针不动,分针旋转了3°
C.时针和分针都没有旋转 D.分针旋转3°,时针旋转角度很小
3. 11:20时分针与时针的夹角是________.
探究点2:旋转的性质
2.旋转的性质
做一做
如图,在硬纸板上,挖出一个三角形ABC,再挖
一个小洞O作为旋转中心,硬纸板下面放一张白
纸。先在纸上描出这个挖掉的三角形图案
(△ABC),然后围绕旋转中心转动硬纸板,再
描出这个挖掉的三角形(△DEF),移开硬纸板.
想一想
(1)旋转中心是________;旋转角有______________________________;
对应点有_________________________;对应线段有_________________________.
(2)在图形的旋转过程中,哪些发生了改变?哪些没有发生改变?
(3)比较对应线段的长短关系,你有什么发现
(4)用量角器来量一量∠AOD、∠BOE、∠COF的大小,比一比它们的大小,你能得出什么结论?
【自主归纳】
旋转的性质:
对应点到旋转中心的距离相等;
每对对应点与旋转中心连线所形成的角都是相等的角,它们都等于旋转角.
旋转不改变图形的大小和形状.
例3:将图案以圆心为中点旋转180°得到的图案是
【归纳总结】根据旋转的性质,旋转前后图形不发生任何变化,绕中心旋转180°,即是对应点绕旋转中心旋转180°.
例4:如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B、A、C’在同一条直线上,则三角板ABC的旋转角度为( )
【针对训练】
1.将数字“6”旋转180°后得到数字“9”,将数字“9”旋转180°后得到数字“6”,现将数字“69”旋转180°后,得到的数字是_________.
探究点3:作图——旋转变换
例5:将△ABC放在每个小正方形为1的网格中,点B、C落在格点上,P是△ABC内部一点,(1)将△ABC绕点A逆时针旋转90°,画出旋转后的图形;
(2)将△APC绕点C顺时针旋转60°,画出旋转后的图形.
(保留作图痕迹)
【归纳总结】旋转作图的步骤:(1)确定旋转中心、旋转方向及旋转角的大小;
(2)确定已知图形的关键点(比如线段的两个端点、三角形的三个顶点等);
(3)确定各关键点的对应点.(将图形的各关键点与旋转中心连接,按规定方向旋转规定角度,找到该点的对应点);(4)按原图顶点的顺序连接各对应点,即得旋转后的图形.
【针对训练】
二、课堂小结
内容
旋转的有关定义 在平面内,将一个图形绕着 沿 转动 , 这样的图形运动称为旋转.其中,这个 叫做旋转的旋转中心,_ _________叫做旋转角.
旋转的性质 对应点到_________的距离相等;每对对应点与旋转中心连线所形成的角都是________的角,它们都等于__________. 旋转不改变图形的________和__________.
1.以下现象中属于旋转的有( )个.
(1)荡秋千 ;(2)火车行驶;(3)方向盘的移动;(4)钟表的摆动;(5)圆规画圆.
A.1 B.2 C.3 D.4
2.时钟上的分针匀速旋转一周需要60min,则经过20min,分针旋转了( )
A.20° B.60° C.90° D.120°
6.学校早上8时开始上课,45分钟后开始下课,这节课分针转动的角度为________.
7.将一个自然数旋转180°后,可以发现一个有趣的现象,有的自然数旋转后还是自然数.例如,808,旋转180°后仍是808,.又如169旋转180°后是691.而有的旋转180°后就不是自然数了,如37.试写出一个旋转180°后仍等于本身的五位数:_______(数字不能完全相同).
8.如图所示,画出三角形ABC绕点C逆时针旋转90°后的图形.(画在图上)
当堂检测参考答案:
1.C 2.D 3.B 4.A
5.17°
6.270°
7.80108
8.如图所示:
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
自主学习
抽象出点的旋转
A
B
(图1)
O
抽象出线的旋转
·
O
A
B
C
D
(图2)
合作探究
·
O
A
B
C
F
D
E
【归纳总结】 本题考查的是旋转的性质,掌握对应点与旋转中心的连线所形成的角等于旋转角是解题的关键.
A.60° B.90° C.120° D.150°
2.如图,将直角三角形ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于__________.
请在途中画出线段AB以O为旋转中心逆时针分别旋转90°,180°,270° 时对应的图形.
当堂检测
3.
4.如图,在直角三角形ABC中,∠BAC=90°,将直角三角形ABC绕点C按逆时针方向旋转48°得到直角三角形A’B’C’,点A在边B’C上,则∠B’的大小为( )
A.42° B.48° C.52° D.58°
5.如图所示,△ABC中,∠BAC=33°,将△ABC绕点A顺时针方向旋转50°,对应得到△AB’C’,则∠B’AC的度数为:___________ .
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
