冀教版(新)八上-13.3 全等三角形的判定 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-13.3 全等三角形的判定 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:08 | ||
图片预览








文档简介
(共32张PPT)
13.3 全等三角形的判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
小明不小心将一块大脸猫的玻璃摔成了三块(如图所示),为了配一块和原来完全一样的玻璃,他带哪一块玻璃就可以了? 你能替他解决这个难题吗? 带着问题我们还是一块儿来学习一下这节的内容吧!
新课精讲
探索新知
1
知识点
判定两三角形全等的基本事实:边角边
问题 1
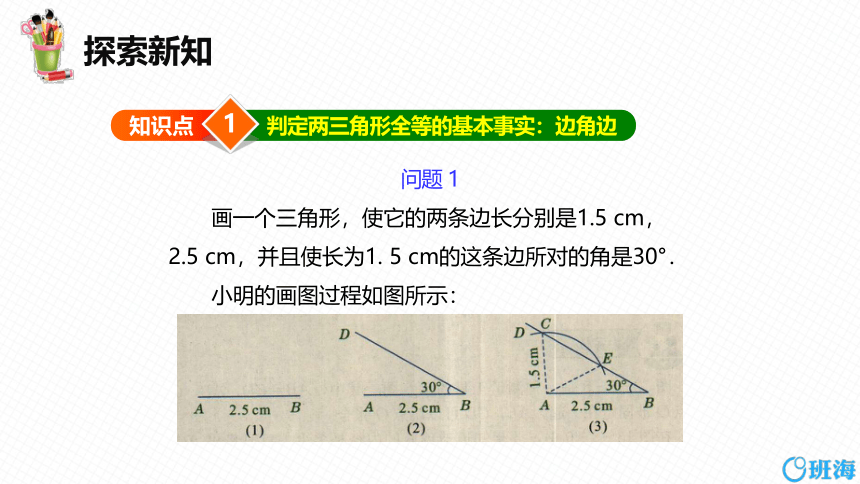
画一个三角形,使它的两条边长分别是1.5 cm,2.5 cm,并且使长为1. 5 cm的这条边所对的角是30°.
小明的画图过程如图所示:
探索新知
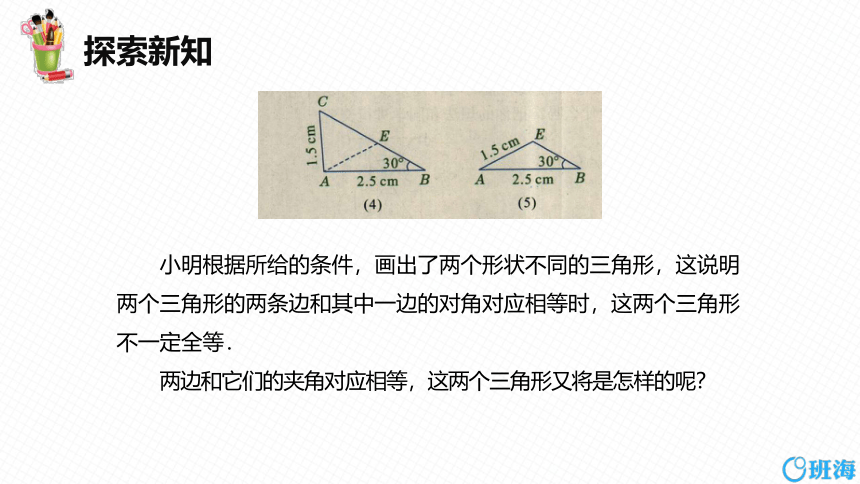
小明根据所给的条件,画出了两个形状不同的三角形,这说明两个三角形的两条边和其中一边的对角对应相等时,这两个三角形不一定全等.
两边和它们的夹角对应相等,这两个三角形又将是怎样的呢?
探索新知
问题 2
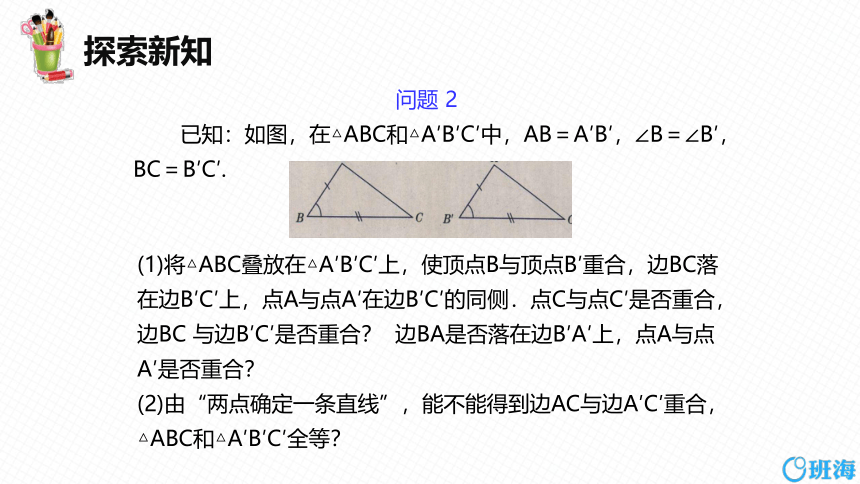
已知:如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,BC=B′C′.
(1)将△ABC叠放在△A′B′C′上,使顶点B与顶点B′重合,边BC落在边B′C′上,点A与点A′在边B′C′的同侧.点C与点C′是否重合,边BC 与边B′C′是否重合? 边BA是否落在边B′A′上,点A与点A′是否重合?
(2)由“两点确定一条直线”,能不能得到边AC与边A′C′重合,△ABC和△A′B′C′全等?
探索新知
归 纳
基本事实二
如果两个三角形的两边和它们的夹角对应相等,那么这两个三角形全等 .
基本事实二可简记为“边角边”或“SAS”.
探索新知
证明书写格式:
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′(SAS) .
要点精析:
(1)相等的元素:两边及这两边的夹角;
(2)在书写两个三角形全等的条件边角边时,要按边、角、边的顺序来写, 即把夹角相等写在中间,以突出两边及其夹角对应相等.
探索新知
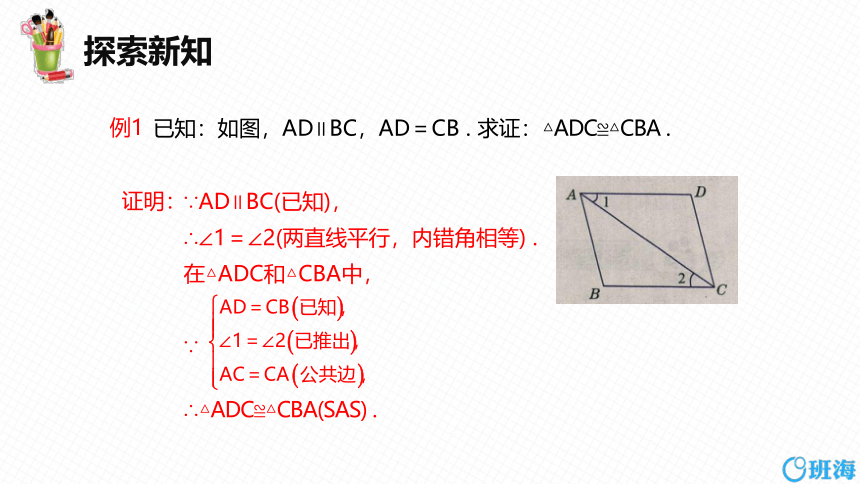
已知:如图,AD∥BC,AD=CB . 求证:△ADC≌△CBA .
例1
证明:
∵AD∥BC(已知),
∴∠1=∠2(两直线平行,内错角相等) .
在△ADC和△CBA中,
∵
∴△ADC≌△CBA(SAS) .
探索新知
总 结
在三角形全等的条件中,要注意“SAS”和“SSA”的区别,“SAS”指的是两边及其夹角对应相等;而“SSA”指的是有两边和一边的对角对应相等,它是不能证明两个三角形全等的.
典题精讲
1 已知:如图,AC=DB,∠ACB=∠DBC.求证:△ABD≌△DCB .
在△ABC和△DCB中,
∵
∴△ABC≌△DCB(SAS).
证明:
典题精讲
2 如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
B
典题精讲
3 如图,AE∥DF,AE=DF,要使 △EAC≌△FDB,需要添加下列选项中的( )
A.AB=CD
B.EC=BF
C.∠A=∠D
D.AB=BC
A
探索新知
2
知识点
判定全等三角形的基本事实:“边角边”的简单应用
图(1)是一种测量工具的示意图.其中,AB=CD,AB,CD的中点O被固定在一起,AB,CD可以绕点O张合.
在图(2)中,要想知道玻璃瓶的内径是多少,只要量出AC的长就可以了. 你知道这是为什么吗 把你的想法和同学进行交流 .
(1)
(2)
【创新应用题】如图,在湖的两岸点A,B之间建一座观赏桥,由于条
件限制,无法直接测量A,B两点之间的距离.
请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求解或推理过程,结果用字母表示).
本题让我们了解了测量两点之间距离的一种方法,设计时,只要需要测量的线段在直线AB一侧便可实施,就可以达到目的.
探索新知
例2
导引:
探索新知
(1)如图所示.
(2)在湖岸上找到可以直接到达点A,B的一点O,
连接BO并延长到点C,使OC=OB;
连接AO并延长到点D,使OD=OA,
连接CD,则测量出CD的长度即为AB的长度.
(3)设CD=m .
∵OD=OA,OC=OB,∠COD=∠BOA,
∴△COD ≌△BOA(SAS).
∴CD=AB,即AB=m .
解:
探索新知
总 结
解答本题的关键是构造全等三角形,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的数量关系.
典题精讲
1 已知:如图,AC,BD相交于点O,且AO=CO,BO=DO.
求证:AB=CD .
在△AOB和△COD中,
∵
∴△AOB≌△COD(SAS).
∴AB=CD . (全等三角形的对应边相等)
证明:
典题精讲
2 如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm
B
典题精讲
3 如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌ △DEF,这个添加的条件可以是AB=_____.
DE
学以致用
小试牛刀
1.两边和它们的______分别相等的两个三角形全等,可以简写成“________”或“______”.其书写模式为:
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′.
夹角
边角边
SAS
AB
∠A′
AC
2.下列三角形中全等的是( )
A.①与② B.②与③
C.①与③ D.①②③
A
4.如图,不添加辅助线,下列条件中可以直接判定
△ABD≌△CBD的是( )
A.AB=CB,∠ADB=∠CDB B.AB=CB,∠A=∠C
C.AB=CB,∠ABD=∠CBD D.AB=CD,∠ADB=∠CDB
小试牛刀
3.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个
条件后,能应用“SAS”判定△ABC≌△DEF( )
A.BF=EC B.∠ACB=∠DFE
C.AC=DF D.∠A=∠D
A
C
小试牛刀
5.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,下列结论不正确的是( )
A.∠BAD=∠CAE B.△ABD≌△ACE
C.AB=BC D.BD=CE
C
6.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形
有( )
A.1对 B.2对
C.3对 D.4对
C
小试牛刀
7.如图是由8个全等的长方形组成的大正方形,线段AB的端点都在小长方形的顶点上,如果点P是某个小长方形的顶点,连接PA,PB,那么使△ABP为等腰直角三角形的点P的个数是( )
A.2个 B.3个
C.4个 D.5个
B
小试牛刀
8.如图,AB∥DE,AB=DE,BE=CF . 求证AC∥DF .
证明:∵AB∥DE,
∴∠B=∠DEF . ∵BE=CF,
∴BE+EC=CF+EC,即BC=EF .
又∵AB=DE ∴△ABC≌△DEF(SAS).
∴∠ACB=∠F . ∴AC∥DF .
小试牛刀
9. 如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D . 求证AC∥DE;
证明:
∴△ABC≌△DFE(SAS).
∴∠ACB=∠DEF.
∴AC∥DE.
在△ABC和△DFE中,
课堂小结
课堂小结
应用“SAS”判定两个三角形全等的“两点注意”:
1. 对应:“SAS”包含“边”“角”两种元素,一定要注意元素的“对应”关系.
2. 顺序:在应用时一定要按边→角→边的顺序排列条件,绝不能出现边→边→角(或角→边→边)的错误,因为边边角(或角边边)不能保证两个三角形全等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
13.3 全等三角形的判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
小明不小心将一块大脸猫的玻璃摔成了三块(如图所示),为了配一块和原来完全一样的玻璃,他带哪一块玻璃就可以了? 你能替他解决这个难题吗? 带着问题我们还是一块儿来学习一下这节的内容吧!
新课精讲
探索新知
1
知识点
判定两三角形全等的基本事实:边角边
问题 1
画一个三角形,使它的两条边长分别是1.5 cm,2.5 cm,并且使长为1. 5 cm的这条边所对的角是30°.
小明的画图过程如图所示:
探索新知
小明根据所给的条件,画出了两个形状不同的三角形,这说明两个三角形的两条边和其中一边的对角对应相等时,这两个三角形不一定全等.
两边和它们的夹角对应相等,这两个三角形又将是怎样的呢?
探索新知
问题 2
已知:如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,BC=B′C′.
(1)将△ABC叠放在△A′B′C′上,使顶点B与顶点B′重合,边BC落在边B′C′上,点A与点A′在边B′C′的同侧.点C与点C′是否重合,边BC 与边B′C′是否重合? 边BA是否落在边B′A′上,点A与点A′是否重合?
(2)由“两点确定一条直线”,能不能得到边AC与边A′C′重合,△ABC和△A′B′C′全等?
探索新知
归 纳
基本事实二
如果两个三角形的两边和它们的夹角对应相等,那么这两个三角形全等 .
基本事实二可简记为“边角边”或“SAS”.
探索新知
证明书写格式:
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′(SAS) .
要点精析:
(1)相等的元素:两边及这两边的夹角;
(2)在书写两个三角形全等的条件边角边时,要按边、角、边的顺序来写, 即把夹角相等写在中间,以突出两边及其夹角对应相等.
探索新知
已知:如图,AD∥BC,AD=CB . 求证:△ADC≌△CBA .
例1
证明:
∵AD∥BC(已知),
∴∠1=∠2(两直线平行,内错角相等) .
在△ADC和△CBA中,
∵
∴△ADC≌△CBA(SAS) .
探索新知
总 结
在三角形全等的条件中,要注意“SAS”和“SSA”的区别,“SAS”指的是两边及其夹角对应相等;而“SSA”指的是有两边和一边的对角对应相等,它是不能证明两个三角形全等的.
典题精讲
1 已知:如图,AC=DB,∠ACB=∠DBC.求证:△ABD≌△DCB .
在△ABC和△DCB中,
∵
∴△ABC≌△DCB(SAS).
证明:
典题精讲
2 如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
B
典题精讲
3 如图,AE∥DF,AE=DF,要使 △EAC≌△FDB,需要添加下列选项中的( )
A.AB=CD
B.EC=BF
C.∠A=∠D
D.AB=BC
A
探索新知
2
知识点
判定全等三角形的基本事实:“边角边”的简单应用
图(1)是一种测量工具的示意图.其中,AB=CD,AB,CD的中点O被固定在一起,AB,CD可以绕点O张合.
在图(2)中,要想知道玻璃瓶的内径是多少,只要量出AC的长就可以了. 你知道这是为什么吗 把你的想法和同学进行交流 .
(1)
(2)
【创新应用题】如图,在湖的两岸点A,B之间建一座观赏桥,由于条
件限制,无法直接测量A,B两点之间的距离.
请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求解或推理过程,结果用字母表示).
本题让我们了解了测量两点之间距离的一种方法,设计时,只要需要测量的线段在直线AB一侧便可实施,就可以达到目的.
探索新知
例2
导引:
探索新知
(1)如图所示.
(2)在湖岸上找到可以直接到达点A,B的一点O,
连接BO并延长到点C,使OC=OB;
连接AO并延长到点D,使OD=OA,
连接CD,则测量出CD的长度即为AB的长度.
(3)设CD=m .
∵OD=OA,OC=OB,∠COD=∠BOA,
∴△COD ≌△BOA(SAS).
∴CD=AB,即AB=m .
解:
探索新知
总 结
解答本题的关键是构造全等三角形,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的数量关系.
典题精讲
1 已知:如图,AC,BD相交于点O,且AO=CO,BO=DO.
求证:AB=CD .
在△AOB和△COD中,
∵
∴△AOB≌△COD(SAS).
∴AB=CD . (全等三角形的对应边相等)
证明:
典题精讲
2 如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm
B
典题精讲
3 如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌ △DEF,这个添加的条件可以是AB=_____.
DE
学以致用
小试牛刀
1.两边和它们的______分别相等的两个三角形全等,可以简写成“________”或“______”.其书写模式为:
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′.
夹角
边角边
SAS
AB
∠A′
AC
2.下列三角形中全等的是( )
A.①与② B.②与③
C.①与③ D.①②③
A
4.如图,不添加辅助线,下列条件中可以直接判定
△ABD≌△CBD的是( )
A.AB=CB,∠ADB=∠CDB B.AB=CB,∠A=∠C
C.AB=CB,∠ABD=∠CBD D.AB=CD,∠ADB=∠CDB
小试牛刀
3.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个
条件后,能应用“SAS”判定△ABC≌△DEF( )
A.BF=EC B.∠ACB=∠DFE
C.AC=DF D.∠A=∠D
A
C
小试牛刀
5.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,下列结论不正确的是( )
A.∠BAD=∠CAE B.△ABD≌△ACE
C.AB=BC D.BD=CE
C
6.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形
有( )
A.1对 B.2对
C.3对 D.4对
C
小试牛刀
7.如图是由8个全等的长方形组成的大正方形,线段AB的端点都在小长方形的顶点上,如果点P是某个小长方形的顶点,连接PA,PB,那么使△ABP为等腰直角三角形的点P的个数是( )
A.2个 B.3个
C.4个 D.5个
B
小试牛刀
8.如图,AB∥DE,AB=DE,BE=CF . 求证AC∥DF .
证明:∵AB∥DE,
∴∠B=∠DEF . ∵BE=CF,
∴BE+EC=CF+EC,即BC=EF .
又∵AB=DE ∴△ABC≌△DEF(SAS).
∴∠ACB=∠F . ∴AC∥DF .
小试牛刀
9. 如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D . 求证AC∥DE;
证明:
∴△ABC≌△DFE(SAS).
∴∠ACB=∠DEF.
∴AC∥DE.
在△ABC和△DFE中,
课堂小结
课堂小结
应用“SAS”判定两个三角形全等的“两点注意”:
1. 对应:“SAS”包含“边”“角”两种元素,一定要注意元素的“对应”关系.
2. 顺序:在应用时一定要按边→角→边的顺序排列条件,绝不能出现边→边→角(或角→边→边)的错误,因为边边角(或角边边)不能保证两个三角形全等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
