冀教版(新)八上-13.4 三角形的尺规作图【优质课件】
文档属性
| 名称 | 冀教版(新)八上-13.4 三角形的尺规作图【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
13.4 三角形的尺规作图
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
用直尺(没有刻度)和圆规作图,是一种具有特殊要求的作图方法 . 这种作图方法不必用具体数值,只按给定图形进行再作图 . 这也是它与画图的区别所在 .
新课精讲
探索新知
1
知识点
尺规作图
我们前面所画的图形大都是用刻度尺、三角尺、量角器和圆规等各种工具画出的.实际上,只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图的方法被称为尺规作图.
我们已经学过的尺规作图有:
作一条线段等于已知线段,作一个角等于已知角. 在这个基础上,我们就可以用尺规作三角形了.
探索新知
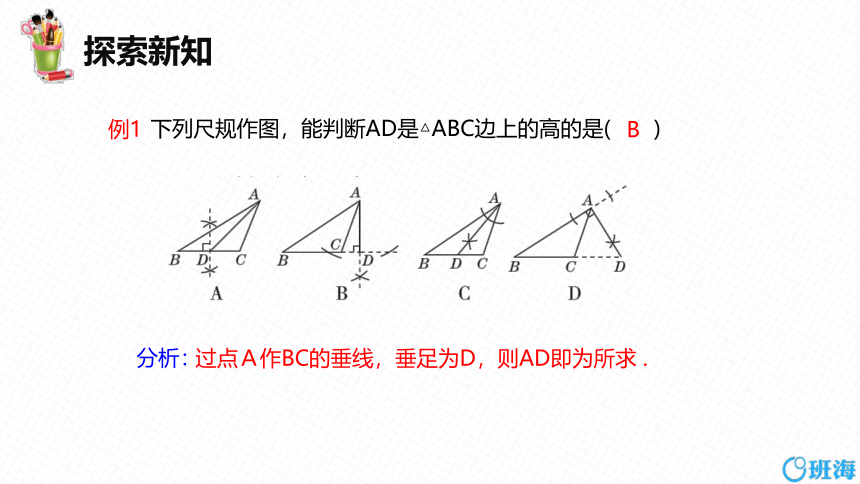
下列尺规作图,能判断AD是△ABC边上的高的是( )
例1
B
分析:
过点A作BC的垂线,垂足为D,则AD即为所求 .
探索新知
总 结
本题考查了作图—复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法 . 解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图 .
1 尺规作图的画图工具是( )
A.刻度尺、圆规
B.三角板和量角器
C.直尺和量角器
D.没有刻度的直尺和圆规
D
典题精讲
典题精讲
2 如图,用尺规作出∠OBF=∠AOB,作图痕迹 是( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
典题精讲
3 下列属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.已知∠α,作∠AOB,使∠AOB=2∠α
C.画线段AC=3 cm
D.用三角板作AB的垂线
B
探索新知
2
知识点
用尺规作三角形
已知三边,用尺规作三角形.
如图,已知线段a,b,c.
求作:△ABC,使AB=c,BC=a,AC=b.
由作一条线段等于已知线段,能够作出边AB,即A,B两点确定. 而BC=a,AC=b . 故以点A为圆心,b为半径画弧,以点B为圆心,a为半径画弧,两弧的交点就是点C .
例2
分析:
探索新知
作法:
第一步:作线段AB等于c.
第二步:以点A为圆心,b为半径画弧.
探索新知
第三步:以点B为圆心,a为半径画弧,两弧交于点C.
第四步:连接AC,BC,△ABC即为所求.
探索新知
总 结
由三角形全等的判定可以知道,每一种判定两个三角形全等的条件(SSS,SAS,ASA,AAS)都只能作出唯一的三角形.
典题精讲
1 已知:线段a,求作△ABC,使AB=BC=AC=a.
如图.
(1)作∠MCN=∠α.
(2)在射线CN,CM上分别截取CA=b,CB=a.
(3)连接AB.
△ABC即为所求做的三角形.
作法:
典题精讲
2 利用基本作图方法,不能作出唯一三角形的是( )
A.已知两边及其夹角
B.已知两角及其夹边
C.已知两边及一边的对角
D.已知三边
C
典题精讲
3 根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=1
D.∠C=90°,AB=6
A
学以致用
小试牛刀
1 . 只用______(没有刻度)和______画图的方法称为尺规作图.已学
过的尺规作图包括:①作一条线段等于__________;②作一个角
等于________ .
直尺
圆规
己知线段
己知角
2.利用尺规作三角形,有几种基本类型:
已知三角形的两边及其夹角,作符合要求的三角形,其依据是“______”;
已知三角形的两角及其夹边,作符合要求的三角形,其依据是“______”;
已知三角形的三边,作符合要求的三角形,其依据是“______ .“
SAS
ASA
SSS
小试牛刀
3 . 已知三边作三角形,用到的基本作图方法是( )
A. 作一个角等于已知角
B. 平分一个已知角
C. 在射线上截取一线段等于已知线段
D. 作一条直线的垂线
C
4 . 如图所示,小敏做题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,
然后粘贴在上面,她作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
C
小试牛刀
5 . 如图,是数轴的一部分,其单位长度为a,已知△ABC中,AB=3a,BC=4a,AC=5a.用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法);
解:如图
小试牛刀
6 . 已知:线段a,c,∠α.求作:△ABC.使BC=a,AB=c,
∠ABC=∠α.
解:(1)作图如下 .
①作∠ABC=∠a,② 作BC=a,AB=c,
③连接AC . △ABC即为所求 .
课堂小结
课堂小结
1.尺规作图的定义:
在几何作图中,把用没有刻度的直尺和圆规作图,简称尺规作图.
注意:尺规作图指的是只用没有刻度的直尺和圆规两种工具.
2.常见的几种尺规作图:
(1)已学到的基本作图:
①作一条线段等于已知线段;②作一个角等于已知角.
(2)作三角形:①已知两边及其夹角作三角形;②已知三边作三角形;③已知两角及其夹边作三角形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
13.4 三角形的尺规作图
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
用直尺(没有刻度)和圆规作图,是一种具有特殊要求的作图方法 . 这种作图方法不必用具体数值,只按给定图形进行再作图 . 这也是它与画图的区别所在 .
新课精讲
探索新知
1
知识点
尺规作图
我们前面所画的图形大都是用刻度尺、三角尺、量角器和圆规等各种工具画出的.实际上,只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图的方法被称为尺规作图.
我们已经学过的尺规作图有:
作一条线段等于已知线段,作一个角等于已知角. 在这个基础上,我们就可以用尺规作三角形了.
探索新知
下列尺规作图,能判断AD是△ABC边上的高的是( )
例1
B
分析:
过点A作BC的垂线,垂足为D,则AD即为所求 .
探索新知
总 结
本题考查了作图—复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法 . 解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图 .
1 尺规作图的画图工具是( )
A.刻度尺、圆规
B.三角板和量角器
C.直尺和量角器
D.没有刻度的直尺和圆规
D
典题精讲
典题精讲
2 如图,用尺规作出∠OBF=∠AOB,作图痕迹 是( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
典题精讲
3 下列属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.已知∠α,作∠AOB,使∠AOB=2∠α
C.画线段AC=3 cm
D.用三角板作AB的垂线
B
探索新知
2
知识点
用尺规作三角形
已知三边,用尺规作三角形.
如图,已知线段a,b,c.
求作:△ABC,使AB=c,BC=a,AC=b.
由作一条线段等于已知线段,能够作出边AB,即A,B两点确定. 而BC=a,AC=b . 故以点A为圆心,b为半径画弧,以点B为圆心,a为半径画弧,两弧的交点就是点C .
例2
分析:
探索新知
作法:
第一步:作线段AB等于c.
第二步:以点A为圆心,b为半径画弧.
探索新知
第三步:以点B为圆心,a为半径画弧,两弧交于点C.
第四步:连接AC,BC,△ABC即为所求.
探索新知
总 结
由三角形全等的判定可以知道,每一种判定两个三角形全等的条件(SSS,SAS,ASA,AAS)都只能作出唯一的三角形.
典题精讲
1 已知:线段a,求作△ABC,使AB=BC=AC=a.
如图.
(1)作∠MCN=∠α.
(2)在射线CN,CM上分别截取CA=b,CB=a.
(3)连接AB.
△ABC即为所求做的三角形.
作法:
典题精讲
2 利用基本作图方法,不能作出唯一三角形的是( )
A.已知两边及其夹角
B.已知两角及其夹边
C.已知两边及一边的对角
D.已知三边
C
典题精讲
3 根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=1
D.∠C=90°,AB=6
A
学以致用
小试牛刀
1 . 只用______(没有刻度)和______画图的方法称为尺规作图.已学
过的尺规作图包括:①作一条线段等于__________;②作一个角
等于________ .
直尺
圆规
己知线段
己知角
2.利用尺规作三角形,有几种基本类型:
已知三角形的两边及其夹角,作符合要求的三角形,其依据是“______”;
已知三角形的两角及其夹边,作符合要求的三角形,其依据是“______”;
已知三角形的三边,作符合要求的三角形,其依据是“______ .“
SAS
ASA
SSS
小试牛刀
3 . 已知三边作三角形,用到的基本作图方法是( )
A. 作一个角等于已知角
B. 平分一个已知角
C. 在射线上截取一线段等于已知线段
D. 作一条直线的垂线
C
4 . 如图所示,小敏做题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,
然后粘贴在上面,她作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
C
小试牛刀
5 . 如图,是数轴的一部分,其单位长度为a,已知△ABC中,AB=3a,BC=4a,AC=5a.用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法);
解:如图
小试牛刀
6 . 已知:线段a,c,∠α.求作:△ABC.使BC=a,AB=c,
∠ABC=∠α.
解:(1)作图如下 .
①作∠ABC=∠a,② 作BC=a,AB=c,
③连接AC . △ABC即为所求 .
课堂小结
课堂小结
1.尺规作图的定义:
在几何作图中,把用没有刻度的直尺和圆规作图,简称尺规作图.
注意:尺规作图指的是只用没有刻度的直尺和圆规两种工具.
2.常见的几种尺规作图:
(1)已学到的基本作图:
①作一条线段等于已知线段;②作一个角等于已知角.
(2)作三角形:①已知两边及其夹角作三角形;②已知三边作三角形;③已知两角及其夹边作三角形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
