冀教版(新)八上-14.1 平方根 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-14.1 平方根 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:08 | ||
图片预览










文档简介
(共31张PPT)
14.1 平方根
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,每个小正方形的边长是1,我们通过剪开,拼接会得到大正方形,我知道小正方形的面积是1,因为右边的大正方形是由左边的两个小正方形剪拼成的,所以大正方形的面积是2. 因为正方形的面积是边长乘一边长,所以a2=2,那么a等于多少呢?我们也就是找一个数,是它的平方等于2,由于正方形的边长是正数,
所以就是找一个正数,使这个正数的平方等于2,我们把a叫做2的算术平方根,如果一个正数x的平方等于a,即x2=a,
那么这个正数x就叫做a的算术平方根.
新课精讲
探索新知
1
知识点
算术平方根的定义
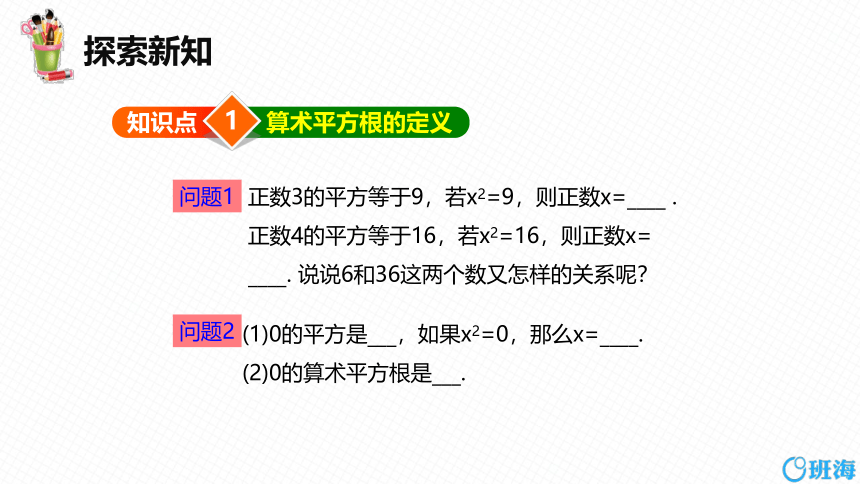
正数3的平方等于9,若x2=9,则正数x=____ .
正数4的平方等于16,若x2=16,则正数x=
____. 说说6和36这两个数又怎样的关系呢?
问题1
问题2
(1)0的平方是___,如果x2=0,那么x=____.
(2)0的算术平方根是___.
探索新知
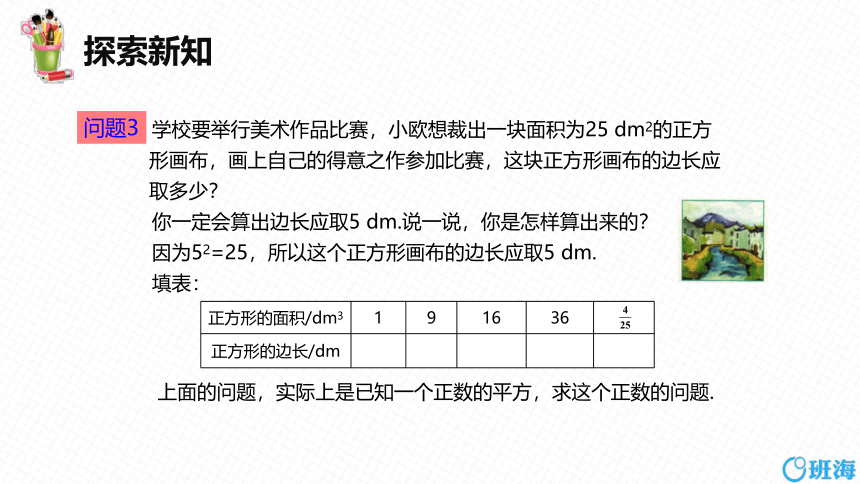
学校要举行美术作品比赛,小欧想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
你一定会算出边长应取5 dm.说一说,你是怎样算出来的?
因为52=25,所以这个正方形画布的边长应取5 dm.
填表:
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
问题3
正方形的面积/dm3 1 9 16 36
正方形的边长/dm
探索新知
结 论
一个正数的两个平方根互为相反数. 我们把一
个正数a的正的平方根 叫做0的算术平方根
(arithmetic square root).
探索新知
下列说法中,正确的是( )
A.9的平方根是±3,应表示为92=±3
B.±3是9的平方根,应表示为± =3
C.把9开平方能得到9的平方根,即 =±3
D.9的算术平方根是3,应表示为 =3
例1
D
导引:先根据每个式子的结构分析其意义,然后根据其意义求值.
探索新知
总 结
必须弄清以下符号的意义:± (a≥0)表示非负数a的平方根, (a≥0)表示非负数a的算术平方根;把非负数a开平方,求它的平方根可用± 表示.
1 的算术平方根是_____ .
2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
典题精讲
3 x是16的算术平方根,那么x的算术平方根是( )
A. 4 B. 2 C. D. ±4
B
探索新知
2
知识点
求算术平方根
当求得一个正数的算术平方根后,它的负的平方
根可相应求得 .
例如,9的算术平方根为3,它的负的平方根就是
-3,即 =3,- =-3.
的算术平方根为 ,它的负的平方根就是- ,
即
0的平方根只有一个,就是0,我们也说0的算术平
方根为0,即 =0 .
探索新知
(1)正数的算术平方根是一个正数;
(2)0的算术平方根是0;
(3)负数没有算术平方根;
(4)被开方数越大,对应的算术平方根也越大;
探索新知
例2 计算下列各式:
(1) (2) (3) (4)
解:
探索新知
(1)求一个数的算术平方根时,首先要弄清是求哪个数的算术平方根,分清求 与81的算术平方根的不同意义,不要被表面现象迷惑.求 的值实质是求81的算术平方根;求的算术平方根实质是求9的算术平方根.
(2)求一个非负数的算术平方根常借助于平方运算,因此熟记常用平方数对求一个数的算术平方根十分有用.
总 结
1 填空:
(1) 的算术平方根是______;
(2)若 =6,则x=________;
(3)若2x+1的算术平方根是2,则x=_____.
4
±6
典题精讲
典题精讲
2 等于( )
A.2 B.3 C.4 D.5
3 设 =a,则下列结论正确的是( )
A.a=441 B.a=4412
C.a=-21 D.a=21
B
D
探索新知
3
知识点
算术平方根的非负性( ≥0,a≥0)
(1)因为___2=64,所以64的算术平方根是____,即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,
即 =______.
(3)因为____2=0,所以0的算术平方根是_____,即 =______.
问题1
问题2
讨论:在 中,被开方数a是一个 数,算术平方根 是一个 数.
探索新知
所以算术平方根 具有双重非负性:①被开方
数a是___,即a≥0;②算术平方根 本身是非负数,
即____.
归 纳
探索新知
(1)算术平方根 具有双重非负性:
①被开方数a是非负数,即a≥0;
②算术平方根是非负数,即 ≥0 .
(2)算术平方根是它本身的数只有0和1 .
探索新知
例3 已知y= +5,求x+y的值.
导引:只有非负数才有算术平方根,由此我们可以得知x-8≥0且8-x≥0,而同时满足这两个条件的x的取值只有x=8,进而求出y的值,x+y的值随即可知.
解:由题意可得x-8≥0且8-x≥0,即x≥8且x≤8 . ∴x=8 .
当x=8时,y=5. ∴x+y=8+5=13 .
探索新知
在一个条件式子中同时含有类似 与 的
式子,即条件式子中被开方数互为相反数,只有它
们都等于0时,这两个式子才都有意义.
总 结
典题精讲
1 设a-2是一个数的算术平方根,那么( )
A.a≥0 B.a>0
C.a>2 D.a≥2
2 下列算式有意义的是( )
A. B.
C. D.
C
D
学以致用
小试牛刀
1 . 已知边长为m的正方形面积为12,则下列说法中,错误的是( )
①m是无理数;
②m是方程m2-12=0的解;
③m满足不等式组;
④m是12的算术平方根.
A. ①② B. ①③ C. ③ D. ①②④
C
小试牛刀
2 . 一个自然数的算术平方根为a,则和这个自然数相邻的下一个
自然数是( )
A. a+1 B. a2+1 C. D.
B
3 . 已知一个表面积为12dm 的正方体,则这个正方体的棱长为( )
A. 1dm B. dm C. dm D. 3dm
B
小试牛刀
4.下列命题中,正确的个数有( )
①1的平方根是1 ;
②1是1的算术平方根;
③( 1)2的平方根是 1;
④0的算术平方根是它本身 .
A.1个 B.2个 C.3个 D.4个
B
小试牛刀
6 . 已知9的算术平方根为a,|b|=4,求a-b的值.
解:9的算术平方根为a,|b|=4,
a= =3,b=4或b=-4,
a-b=3-4=-1,a-b=3-(-4)=7,∴a-b的值是-1或7.
5 . 已知x,y都是有理数,且y= + +3,求2x-y的值 .
解:由题意得2-x=0,解得x=2 .
所以y=3.因此2x-y=2x2-3=1 .
课堂小结
课堂小结
通过这节课的学习,我们要掌握以下的内容:
(1)算术平方根的概念,式子 中的双重非负性:一是a≥0,二是 ≥0.
(2)算术平方根的性质:一个正数的算术平方根是一个正数;0的算术平方根是0;负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
14.1 平方根
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,每个小正方形的边长是1,我们通过剪开,拼接会得到大正方形,我知道小正方形的面积是1,因为右边的大正方形是由左边的两个小正方形剪拼成的,所以大正方形的面积是2. 因为正方形的面积是边长乘一边长,所以a2=2,那么a等于多少呢?我们也就是找一个数,是它的平方等于2,由于正方形的边长是正数,
所以就是找一个正数,使这个正数的平方等于2,我们把a叫做2的算术平方根,如果一个正数x的平方等于a,即x2=a,
那么这个正数x就叫做a的算术平方根.
新课精讲
探索新知
1
知识点
算术平方根的定义
正数3的平方等于9,若x2=9,则正数x=____ .
正数4的平方等于16,若x2=16,则正数x=
____. 说说6和36这两个数又怎样的关系呢?
问题1
问题2
(1)0的平方是___,如果x2=0,那么x=____.
(2)0的算术平方根是___.
探索新知
学校要举行美术作品比赛,小欧想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
你一定会算出边长应取5 dm.说一说,你是怎样算出来的?
因为52=25,所以这个正方形画布的边长应取5 dm.
填表:
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
问题3
正方形的面积/dm3 1 9 16 36
正方形的边长/dm
探索新知
结 论
一个正数的两个平方根互为相反数. 我们把一
个正数a的正的平方根 叫做0的算术平方根
(arithmetic square root).
探索新知
下列说法中,正确的是( )
A.9的平方根是±3,应表示为92=±3
B.±3是9的平方根,应表示为± =3
C.把9开平方能得到9的平方根,即 =±3
D.9的算术平方根是3,应表示为 =3
例1
D
导引:先根据每个式子的结构分析其意义,然后根据其意义求值.
探索新知
总 结
必须弄清以下符号的意义:± (a≥0)表示非负数a的平方根, (a≥0)表示非负数a的算术平方根;把非负数a开平方,求它的平方根可用± 表示.
1 的算术平方根是_____ .
2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
典题精讲
3 x是16的算术平方根,那么x的算术平方根是( )
A. 4 B. 2 C. D. ±4
B
探索新知
2
知识点
求算术平方根
当求得一个正数的算术平方根后,它的负的平方
根可相应求得 .
例如,9的算术平方根为3,它的负的平方根就是
-3,即 =3,- =-3.
的算术平方根为 ,它的负的平方根就是- ,
即
0的平方根只有一个,就是0,我们也说0的算术平
方根为0,即 =0 .
探索新知
(1)正数的算术平方根是一个正数;
(2)0的算术平方根是0;
(3)负数没有算术平方根;
(4)被开方数越大,对应的算术平方根也越大;
探索新知
例2 计算下列各式:
(1) (2) (3) (4)
解:
探索新知
(1)求一个数的算术平方根时,首先要弄清是求哪个数的算术平方根,分清求 与81的算术平方根的不同意义,不要被表面现象迷惑.求 的值实质是求81的算术平方根;求的算术平方根实质是求9的算术平方根.
(2)求一个非负数的算术平方根常借助于平方运算,因此熟记常用平方数对求一个数的算术平方根十分有用.
总 结
1 填空:
(1) 的算术平方根是______;
(2)若 =6,则x=________;
(3)若2x+1的算术平方根是2,则x=_____.
4
±6
典题精讲
典题精讲
2 等于( )
A.2 B.3 C.4 D.5
3 设 =a,则下列结论正确的是( )
A.a=441 B.a=4412
C.a=-21 D.a=21
B
D
探索新知
3
知识点
算术平方根的非负性( ≥0,a≥0)
(1)因为___2=64,所以64的算术平方根是____,即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,
即 =______.
(3)因为____2=0,所以0的算术平方根是_____,即 =______.
问题1
问题2
讨论:在 中,被开方数a是一个 数,算术平方根 是一个 数.
探索新知
所以算术平方根 具有双重非负性:①被开方
数a是___,即a≥0;②算术平方根 本身是非负数,
即____.
归 纳
探索新知
(1)算术平方根 具有双重非负性:
①被开方数a是非负数,即a≥0;
②算术平方根是非负数,即 ≥0 .
(2)算术平方根是它本身的数只有0和1 .
探索新知
例3 已知y= +5,求x+y的值.
导引:只有非负数才有算术平方根,由此我们可以得知x-8≥0且8-x≥0,而同时满足这两个条件的x的取值只有x=8,进而求出y的值,x+y的值随即可知.
解:由题意可得x-8≥0且8-x≥0,即x≥8且x≤8 . ∴x=8 .
当x=8时,y=5. ∴x+y=8+5=13 .
探索新知
在一个条件式子中同时含有类似 与 的
式子,即条件式子中被开方数互为相反数,只有它
们都等于0时,这两个式子才都有意义.
总 结
典题精讲
1 设a-2是一个数的算术平方根,那么( )
A.a≥0 B.a>0
C.a>2 D.a≥2
2 下列算式有意义的是( )
A. B.
C. D.
C
D
学以致用
小试牛刀
1 . 已知边长为m的正方形面积为12,则下列说法中,错误的是( )
①m是无理数;
②m是方程m2-12=0的解;
③m满足不等式组;
④m是12的算术平方根.
A. ①② B. ①③ C. ③ D. ①②④
C
小试牛刀
2 . 一个自然数的算术平方根为a,则和这个自然数相邻的下一个
自然数是( )
A. a+1 B. a2+1 C. D.
B
3 . 已知一个表面积为12dm 的正方体,则这个正方体的棱长为( )
A. 1dm B. dm C. dm D. 3dm
B
小试牛刀
4.下列命题中,正确的个数有( )
①1的平方根是1 ;
②1是1的算术平方根;
③( 1)2的平方根是 1;
④0的算术平方根是它本身 .
A.1个 B.2个 C.3个 D.4个
B
小试牛刀
6 . 已知9的算术平方根为a,|b|=4,求a-b的值.
解:9的算术平方根为a,|b|=4,
a= =3,b=4或b=-4,
a-b=3-4=-1,a-b=3-(-4)=7,∴a-b的值是-1或7.
5 . 已知x,y都是有理数,且y= + +3,求2x-y的值 .
解:由题意得2-x=0,解得x=2 .
所以y=3.因此2x-y=2x2-3=1 .
课堂小结
课堂小结
通过这节课的学习,我们要掌握以下的内容:
(1)算术平方根的概念,式子 中的双重非负性:一是a≥0,二是 ≥0.
(2)算术平方根的性质:一个正数的算术平方根是一个正数;0的算术平方根是0;负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
