冀教版(新)八上-14.2 立方根【优质课件】
文档属性
| 名称 | 冀教版(新)八上-14.2 立方根【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:08 | ||
图片预览










文档简介
(共40张PPT)
14.2 立方根
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
这是由8个同样大小的单位立方体组成的魔方,这8个单位立方体可以重新排列,组成魔方表面的各种不同图案 .
新课精讲
探索新知
1
知识点
立方根
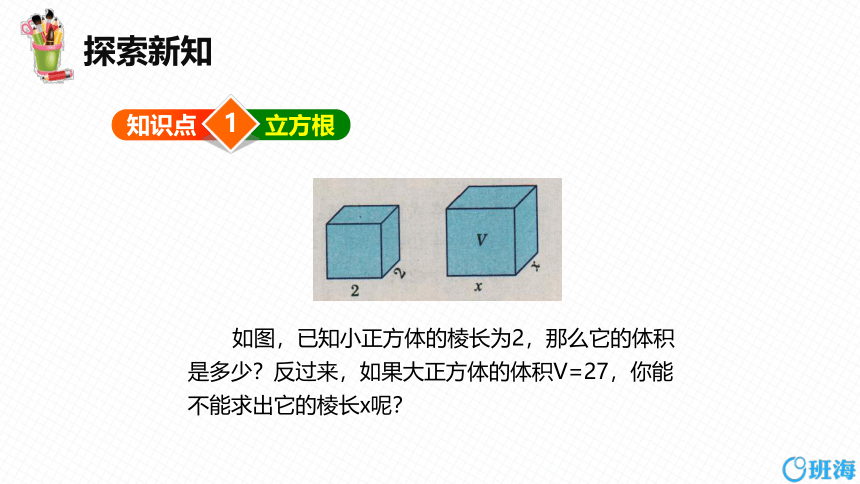
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
探索新知
求满足下列各式的x的值:
(1)x3=-1; (2)x3=64; (3)x3=0.008; (4)x3 =-
问题
小亮是这样想的:由已知小正方体的棱长为2,可以求出它的体积为23 = 8;同样,根据正方体的体公式以及立方运算,由大正方体的体积,也可以求出它的棱长.
他是这样做的:因为33=27,所以,这个大正方体的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么做的?
探索新知
结 论
一般地,如果一个数x的立方等于a,即x3=a,
那么这个数x就叫做a的立方根(cube root),也叫
做a的三次方根.
例如,-1的立方根为-1,64的立方根为4,
0.008的立方根为0.2,- 的立方根为-
探索新知
立方根:一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.
表示方法:一个数a的立方根,用符号“ ”
表示,读作“三次根号a”,其中a是被开方数,3是根指数.
探索新知
下列说法正确的是( )
A. 负数没有立方根
B. -9的立方根是
=3
任何正数都有两个立方根,它们互为相反数
例1
B
解析:任何一个数都有唯一的立方根,所以选项A,D不正确,因为33=27,所以 ≠3,故选项C也不正确,选项B正确.
探索新知
总 结
1.判断一个数x是不是某数a的立方根,就看x3是不是等于a .
2.求一个数的立方根,应先找到一个立方等于所求数的数,再求立方根 .
典题精讲
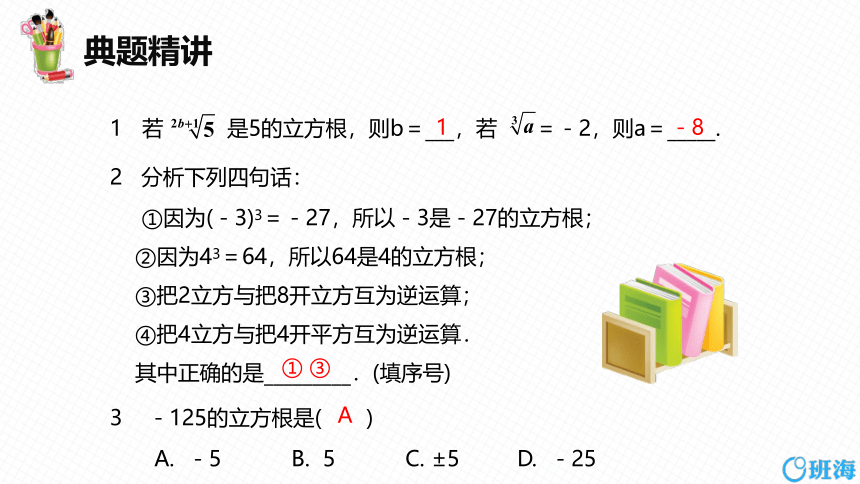
若 是5的立方根,则b=___,若 =-2,则a=_____.
2 分析下列四句话:
①因为(-3)3=-27,所以-3是-27的立方根;
②因为43=64,所以64是4的立方根;
③把2立方与把8开立方互为逆运算;
④把4立方与把4开平方互为逆运算.
其中正确的是_________.(填序号)
1
-8
① ③
3 -125的立方根是( )
A. -5 B. 5 C. ±5 D. -25
A
探索新知
2
知识点
立方根的性质
根据立方根的意义填空,看看正数、0、负数的立方根各有什么特点?
1. 因为23=8,所以8的立方根是 ( );
2. 因为(0.5)3=0.125,所以0.125的立方根是( );
3.因为(0)3 =0,所以0的立方根是( );
4.因为(-2)3 =-8,所以8的立方根是( );
5.因为 ,所以 的立方根是( ).
问题
探索新知
结 论
一个正数有一个正的立方根 .
一个负数有一个负的立方根 .
0的立方根是0 .
探索新知
例2 求下列各数的立方根:
(1) (2) -8; (3)-0.064 .
解:
(1)因为 ,所以 的立方根为 ,即
(2)因为(-2)3 =-8,所以-8的立方根为-2,即 =-2 .
(3)因为(-0.4)3 =-0.064,所以-0.064的立方根为-0.4,即 =-0. 4 .
易见:
探索新知
如果被开方数为带分数,一般先将被开方数化为假分数,然后再求其立方根.求一个数的立方根时要注意结果的正负.
总 结
典题精讲
求下列各数的立方根:
(1)-125; (2)- ; (3)2 ; (4)-0.008 .
解:(1)因为(-5)3=-125,所以-125的立方根是-5,即 =-5 .
(2)因为 ,所以- 的立方根是- ,即
(3)因为 ,而 ,所以 的立方根是 ,即
(4)因为(-0.2)3=-0.008,所以-0.008的立方根是-0.2,即 =-0.2 .
典题精讲
2 下列说法正确的是( )
A.0.8的立方根是0.2 B.1的立方根为±1
C.-1的立方根是-1 D.-25没有立方根
C
3 下列说法:
①负数没有立方根;
②一个数的立方根不是正数就是负数;
③一个正数或负数的立方根和这个数同号,0的立方根是0;
④如果一个数的立方根是这个数本身,那么这个数必是1或0 .
其中错误的是( )
A.①②③ B.①②④ C.②③④ D.①③④
B
探索新知
3
知识点
求立方根(开平方)
1.因为(3)3=27,所以 =___.
2.因为(-4)3=-64,所以 =____.
3.因为x3=a,所以 =____.
探索新知
求一个数立方根的运算,叫做开立方. 开立方与立方也是互逆运算 .
结 论
探索新知
开立方:求一个数的立方根的运算,叫做开立方.
要点精析:(1)任何一个数都有立方根,而负数没有平方根.
(2)开立方与立方互为逆运算,我们可以通过立方来求一个数的立方根.
探索新知
例3 求下列各式的值:
解:
探索新知
利用立方运算求一个的立方根,要注意正数有一个正的立方根,负数有一个负的立方根,0的立方根是0.
总 结
典题精讲
1 计算:
解:
典题精讲
2 下列各式中,正确的是( )
A. =±2 B. =5
C. =±2 D. =5
3 的算术平方根是( )
A.2 B.±2
C. D.±
C
B
探索新知
3
知识点
( )3与 的性质
性质:(1)一个正数有一个正的立方根;(2)一个负数有一个负的立方根;(3)0的立方根是0;(4) =a;(5)
要点精析:(1)互为相反数的数的立方根也互为相反数;
(2)利用 ,可以把求一个负数的立方根转化为求一个正数的立方根的相反数.
探索新知
例4 已知 =1-a2,求a的值.
导引:这是关于“一个数的立方根等于它本身”的题,因此只需找出立方根等于本身的数即可.
解:一个数的立方根等于它本身的数有0,1,-1 .
当1-a2=0时,a2=1,则a=±1;
当1-a2=1时,a2=0,则a=0;
当1-a2=-1时,a2=2,则a=±
综上,a的值为:±1,± ,0 .
探索新知
根据立方根的意义解决问题,关键要将式子的意义用立方根翻译出来,如本题就是“立方根等于本身”.
总 结
典题精讲
若 与 互为相反数且y≠0,求 的值.
解:由题意,得
又因为 ,
所以 ,所以1-2x=2-3y,
即2x+1=3y.
又因为y≠0,所以 =3 .
典题精讲
2 若x<0,则 等于( )
A.x B.2x
C.0 D.-2x
3 当a取__________时, 有意义.
任意数
D
学以致用
小试牛刀
1 . 下列判断中,错误的有( )
(1)有立方根的数必有平方根
(2)有平方根的数必有立方根
(3)零的平方根、立方根、算术平方根都是零
(4)不论a是什么实数, 必有意义.
A.1个 B.2个 C.3个 D.4个
A
小试牛刀
2 . 下列说法错误的是( )
A.1是(-1) 的算术平方根 B.0的平方根是0
C.-27的立方根是-3 D. =±13
D
3 . 下列说法正确的是( )
A.负数没有立方根
B.一个数有两个立方根
C.如果一个数有立方根,那么它一定有平方根
D.一个数的立方根与被开方数同号
D
小试牛刀
4 . 求下列各式中的x:
(1)4x2=9; (2)(2x-1)3=-8.
4
9
2
3
1
2
解:(1)4x2=9;
变形得:x2= ,
开方得:x=± ,
解:(2)开立方得:2x-1=-2,
解得:x=- .
小试牛刀
5 . 要制作一个体积为512cm 的正方体形状的包装箱,这个包装箱的
边长应该是( )
A.6cm B.±6cm C.8cm D.±8cm
C
6 . 下列说法中,正确的是( )
A.-4的算术平方根是2 B.- 是2的一个平方根
C.(-1)2的立方根是-1 D. =±5
B
小试牛刀
7 . 已知4x-37的立方根为3,试求2x+4的平方根和算数平方根 .
解:4x-37的立方根为3
4x-37=3
4x=27+37
4x=64
x=16
2x+4=36 平方根=±6 算数平方根=6
课堂小结
课堂小结
平方根 立方根
区别 定义 一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根 一般地,如果一个数x的立方等于a,即x3=a,那么这个数x叫做a的立方根
性质 正数有两个平方根,它们互为相反数 正数有一个立方根,仍为正数
负数没有平方根 负数有一个立方根,仍为负数
表示法 ± (a≥0) (a为任意数)
联系 ①开平方与开立方都与相应的乘方运算互为逆运算 ②0的平方根和立方根都是0 平方根与立方根的区别与联系:
课堂小结
求一个负数的立方根的方法:先求出这个负数的绝对值的立方根,然后再取它的相反数即可;其实质是利用互为相反数的两个数的立方根互为相反数,即 来求解;也就是说三次根号内的负号可以移到三次根号外面.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
14.2 立方根
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
这是由8个同样大小的单位立方体组成的魔方,这8个单位立方体可以重新排列,组成魔方表面的各种不同图案 .
新课精讲
探索新知
1
知识点
立方根
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
探索新知
求满足下列各式的x的值:
(1)x3=-1; (2)x3=64; (3)x3=0.008; (4)x3 =-
问题
小亮是这样想的:由已知小正方体的棱长为2,可以求出它的体积为23 = 8;同样,根据正方体的体公式以及立方运算,由大正方体的体积,也可以求出它的棱长.
他是这样做的:因为33=27,所以,这个大正方体的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么做的?
探索新知
结 论
一般地,如果一个数x的立方等于a,即x3=a,
那么这个数x就叫做a的立方根(cube root),也叫
做a的三次方根.
例如,-1的立方根为-1,64的立方根为4,
0.008的立方根为0.2,- 的立方根为-
探索新知
立方根:一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.
表示方法:一个数a的立方根,用符号“ ”
表示,读作“三次根号a”,其中a是被开方数,3是根指数.
探索新知
下列说法正确的是( )
A. 负数没有立方根
B. -9的立方根是
=3
任何正数都有两个立方根,它们互为相反数
例1
B
解析:任何一个数都有唯一的立方根,所以选项A,D不正确,因为33=27,所以 ≠3,故选项C也不正确,选项B正确.
探索新知
总 结
1.判断一个数x是不是某数a的立方根,就看x3是不是等于a .
2.求一个数的立方根,应先找到一个立方等于所求数的数,再求立方根 .
典题精讲
若 是5的立方根,则b=___,若 =-2,则a=_____.
2 分析下列四句话:
①因为(-3)3=-27,所以-3是-27的立方根;
②因为43=64,所以64是4的立方根;
③把2立方与把8开立方互为逆运算;
④把4立方与把4开平方互为逆运算.
其中正确的是_________.(填序号)
1
-8
① ③
3 -125的立方根是( )
A. -5 B. 5 C. ±5 D. -25
A
探索新知
2
知识点
立方根的性质
根据立方根的意义填空,看看正数、0、负数的立方根各有什么特点?
1. 因为23=8,所以8的立方根是 ( );
2. 因为(0.5)3=0.125,所以0.125的立方根是( );
3.因为(0)3 =0,所以0的立方根是( );
4.因为(-2)3 =-8,所以8的立方根是( );
5.因为 ,所以 的立方根是( ).
问题
探索新知
结 论
一个正数有一个正的立方根 .
一个负数有一个负的立方根 .
0的立方根是0 .
探索新知
例2 求下列各数的立方根:
(1) (2) -8; (3)-0.064 .
解:
(1)因为 ,所以 的立方根为 ,即
(2)因为(-2)3 =-8,所以-8的立方根为-2,即 =-2 .
(3)因为(-0.4)3 =-0.064,所以-0.064的立方根为-0.4,即 =-0. 4 .
易见:
探索新知
如果被开方数为带分数,一般先将被开方数化为假分数,然后再求其立方根.求一个数的立方根时要注意结果的正负.
总 结
典题精讲
求下列各数的立方根:
(1)-125; (2)- ; (3)2 ; (4)-0.008 .
解:(1)因为(-5)3=-125,所以-125的立方根是-5,即 =-5 .
(2)因为 ,所以- 的立方根是- ,即
(3)因为 ,而 ,所以 的立方根是 ,即
(4)因为(-0.2)3=-0.008,所以-0.008的立方根是-0.2,即 =-0.2 .
典题精讲
2 下列说法正确的是( )
A.0.8的立方根是0.2 B.1的立方根为±1
C.-1的立方根是-1 D.-25没有立方根
C
3 下列说法:
①负数没有立方根;
②一个数的立方根不是正数就是负数;
③一个正数或负数的立方根和这个数同号,0的立方根是0;
④如果一个数的立方根是这个数本身,那么这个数必是1或0 .
其中错误的是( )
A.①②③ B.①②④ C.②③④ D.①③④
B
探索新知
3
知识点
求立方根(开平方)
1.因为(3)3=27,所以 =___.
2.因为(-4)3=-64,所以 =____.
3.因为x3=a,所以 =____.
探索新知
求一个数立方根的运算,叫做开立方. 开立方与立方也是互逆运算 .
结 论
探索新知
开立方:求一个数的立方根的运算,叫做开立方.
要点精析:(1)任何一个数都有立方根,而负数没有平方根.
(2)开立方与立方互为逆运算,我们可以通过立方来求一个数的立方根.
探索新知
例3 求下列各式的值:
解:
探索新知
利用立方运算求一个的立方根,要注意正数有一个正的立方根,负数有一个负的立方根,0的立方根是0.
总 结
典题精讲
1 计算:
解:
典题精讲
2 下列各式中,正确的是( )
A. =±2 B. =5
C. =±2 D. =5
3 的算术平方根是( )
A.2 B.±2
C. D.±
C
B
探索新知
3
知识点
( )3与 的性质
性质:(1)一个正数有一个正的立方根;(2)一个负数有一个负的立方根;(3)0的立方根是0;(4) =a;(5)
要点精析:(1)互为相反数的数的立方根也互为相反数;
(2)利用 ,可以把求一个负数的立方根转化为求一个正数的立方根的相反数.
探索新知
例4 已知 =1-a2,求a的值.
导引:这是关于“一个数的立方根等于它本身”的题,因此只需找出立方根等于本身的数即可.
解:一个数的立方根等于它本身的数有0,1,-1 .
当1-a2=0时,a2=1,则a=±1;
当1-a2=1时,a2=0,则a=0;
当1-a2=-1时,a2=2,则a=±
综上,a的值为:±1,± ,0 .
探索新知
根据立方根的意义解决问题,关键要将式子的意义用立方根翻译出来,如本题就是“立方根等于本身”.
总 结
典题精讲
若 与 互为相反数且y≠0,求 的值.
解:由题意,得
又因为 ,
所以 ,所以1-2x=2-3y,
即2x+1=3y.
又因为y≠0,所以 =3 .
典题精讲
2 若x<0,则 等于( )
A.x B.2x
C.0 D.-2x
3 当a取__________时, 有意义.
任意数
D
学以致用
小试牛刀
1 . 下列判断中,错误的有( )
(1)有立方根的数必有平方根
(2)有平方根的数必有立方根
(3)零的平方根、立方根、算术平方根都是零
(4)不论a是什么实数, 必有意义.
A.1个 B.2个 C.3个 D.4个
A
小试牛刀
2 . 下列说法错误的是( )
A.1是(-1) 的算术平方根 B.0的平方根是0
C.-27的立方根是-3 D. =±13
D
3 . 下列说法正确的是( )
A.负数没有立方根
B.一个数有两个立方根
C.如果一个数有立方根,那么它一定有平方根
D.一个数的立方根与被开方数同号
D
小试牛刀
4 . 求下列各式中的x:
(1)4x2=9; (2)(2x-1)3=-8.
4
9
2
3
1
2
解:(1)4x2=9;
变形得:x2= ,
开方得:x=± ,
解:(2)开立方得:2x-1=-2,
解得:x=- .
小试牛刀
5 . 要制作一个体积为512cm 的正方体形状的包装箱,这个包装箱的
边长应该是( )
A.6cm B.±6cm C.8cm D.±8cm
C
6 . 下列说法中,正确的是( )
A.-4的算术平方根是2 B.- 是2的一个平方根
C.(-1)2的立方根是-1 D. =±5
B
小试牛刀
7 . 已知4x-37的立方根为3,试求2x+4的平方根和算数平方根 .
解:4x-37的立方根为3
4x-37=3
4x=27+37
4x=64
x=16
2x+4=36 平方根=±6 算数平方根=6
课堂小结
课堂小结
平方根 立方根
区别 定义 一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根 一般地,如果一个数x的立方等于a,即x3=a,那么这个数x叫做a的立方根
性质 正数有两个平方根,它们互为相反数 正数有一个立方根,仍为正数
负数没有平方根 负数有一个立方根,仍为负数
表示法 ± (a≥0) (a为任意数)
联系 ①开平方与开立方都与相应的乘方运算互为逆运算 ②0的平方根和立方根都是0 平方根与立方根的区别与联系:
课堂小结
求一个负数的立方根的方法:先求出这个负数的绝对值的立方根,然后再取它的相反数即可;其实质是利用互为相反数的两个数的立方根互为相反数,即 来求解;也就是说三次根号内的负号可以移到三次根号外面.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
