冀教版(新)八上-14.3 实数 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-14.3 实数 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:08 | ||
图片预览







文档简介
(共29张PPT)
14.3 实数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
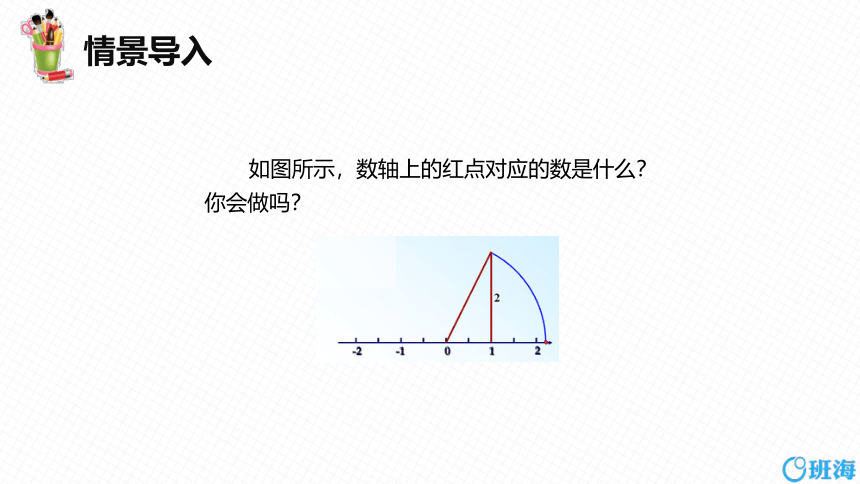
情景导入
如图所示,数轴上的红点对应的数是什么? 你会做吗?
新课精讲
探索新知
1
知识点
实数与数轴的关系
1.如图1所示,将面积分别为2和3的两个正方形放置在数轴上,使得正方形的一个顶点和原点O重合,一条边恰好落在数轴正方向上,其另一个顶点分别为数轴上的点A和点B .
(1)线段OA,OB的长分别是多少?
(2)点A,B在数轴上对应的数分别是哪两个数?
探索新知
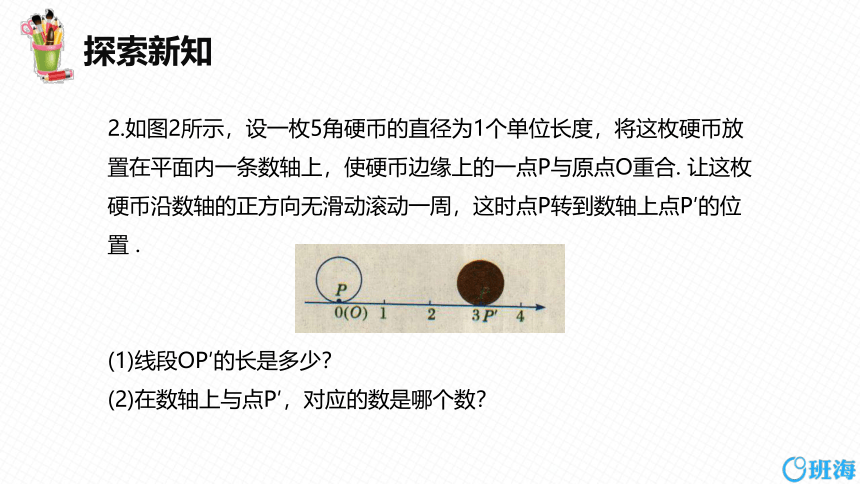
2.如图2所示,设一枚5角硬币的直径为1个单位长度,将这枚硬币放置在平面内一条数轴上,使硬币边缘上的一点P与原点O重合. 让这枚硬币沿数轴的正方向无滑动滚动一周,这时点P转到数轴上点P′的位置 .
(1)线段OP′的长是多少?
(2)在数轴上与点P′,对应的数是哪个数?
探索新知
实际上,图1中小正方形的边长是 ,所以线段OA的长为 ,与点A对应的数是 ;同理,线段OB的长为 ,与点B对应的数是 ;图2中线段OP′的长等于π,与点P′对应的数是π .
由此可知,无理数 , ,π可以用数轴上的点来表示 . 在图1所示的数轴上,按负方向取点A′,使OA′ =OA,则点A对应的数是- .
同理可知,无理数- ,-π也可以用数轴上的点来表示 . 事实上,每个有理数或无理数都可以用数轴上的一个点来表示;反过来,数轴上的点表示的数是有理数或无理数 .
探索新知
结 论
实数和数轴上的点是一一对应(one-to-one correspon-Dence)的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
探索新知
实数与数轴间的关系:
实数与数轴上的点是一一对应的.
它包含着两层含义:
(1)每一个实数都可以用数轴上的一个点来表示;
(2)数轴上的每一个点都表示一个实数.
探索新知
导引:比较一组实数的大小和比较一组有理数的大小一样,可先求出其中无理数的近似数,再将这些数在数轴上表示出来,然后根据“在数轴上右边的点表示的数总比左边的点表示的数大”求解.
解:将各数的大致位置在数轴上表示出来,如图所示.
由图可知,各数用“<”可以连接成:-2 <- <0< <2.5 .
用“<”连接下列各数:- , ,-2 , 2.5 , 0 .
例1
探索新知
总 结
根据“实数与数轴上的点是一一对应的”,并且“在数轴上右边的点表示的数总比左边的点表示的数大”,我们可以利用数形结合思想比较实数的大小.
典题精讲
实数a,b在数轴上的对应点的位置如图所示,把-a,-b,0按照从小到大的顺序排列,正确的是( )
A.-a<0<-b
B.0<-a<-b
C.-b<0<-a
D.0<-b<-a
C
典题精讲
2 和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
A.a<0 B.ab<0
C.aD
D
探索新知
2
知识点
实数的性质
参照有理数的有关概念,谈谈实数的下列概念:
(1) 实数的绝对值 .
(2) 互为相反数的实数 .
(3) —个实数的倒数 .
探索新知
结 论
一个正实数的绝对值是它本身.
一个负实数的绝对值是它的相反数.
0的绝对值是0.
探索新知
在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
(1)相反数:实数a的相反数为-a,若a,b互为相反数,则a+b=0;
(2)非零实数a的倒数为 ,若a,b互为倒数,则ab=1;
(3)绝对值:一个正实数的绝对值是它本身,一个负实数的绝对值是它的相反数,0的绝对值是0.
即:|a|=
探索新知
例2 (1)分别写出- ,π-3.14的相反数;
(2)指出- ,1- 分别是什么数的相反数;
解:(1)因为 ,-(π-3.14) =3.14-π,所以,- ,π-3.14的相反数分别为 , 3.14-π .
(2)因为
所以 分别是 的相反数 .
探索新知
(4)因为
所以绝对值为 的数是 或- .
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数 .
解:(3)因为
所以
典题精讲
1 把下列各数分别填入相应的圈内:
正实数
负实数
有理数
无理数
…
…
…
…
解:正实数:
负实数:
有理数:
无理数:
典题精讲
2 是 的( )
A.相反数 B.倒数
C.负平方根 D.绝对值
3 2- 的绝对值是( )
A.2- B. -2
C.2+ D.±(2- )
A
B
学以致用
小试牛刀
1 . 关于 的叙述,错误的是( )
是有理数 B. 面积为12的正方形边长是
C. 是12的算术平方根 D. 在数轴上可以找到表示 的点
2 . 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A. π-1 B. -π-1
C. -π-1或π-1 D. -π-1或π+1
A
C
小试牛刀
3 . 当a为实数时, =-a,则实数a的数轴上的对应点( ) A.原点的右侧 B.原点的左侧
C.原点或原点的右侧 D.原点或原点的左侧
D
4 . - 的绝对值是( )
A. B. C. - D. 5
C
小试牛刀
5 . 在实数范围内,下列判断正确的是( )
A.若|x|=|y|,则x=y
B.若|x|=( ) ,则x=y
C.若x>y,则x >y
D.若 > ,则x>y
D
小试牛刀
6 . 实数a、b、c在数轴上对应点的位置如图所示,
化简
解:由数轴可知a所以a<0,a-b<0,c-a>0,b-a>0,
所以原式=|a|+(a-b)+c-a+|b-a|
=-a+a-b+c-a+b-a
=c-2a .
课堂小结
课堂小结
1.当数的范围从有理数扩充到实数后,有理数中关于相反数、倒数和绝对值的相关性质同样适用于实数.
2.实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上一个点来表示,反过来数轴上任何一个点都表示一个实数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
14.3 实数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,数轴上的红点对应的数是什么? 你会做吗?
新课精讲
探索新知
1
知识点
实数与数轴的关系
1.如图1所示,将面积分别为2和3的两个正方形放置在数轴上,使得正方形的一个顶点和原点O重合,一条边恰好落在数轴正方向上,其另一个顶点分别为数轴上的点A和点B .
(1)线段OA,OB的长分别是多少?
(2)点A,B在数轴上对应的数分别是哪两个数?
探索新知
2.如图2所示,设一枚5角硬币的直径为1个单位长度,将这枚硬币放置在平面内一条数轴上,使硬币边缘上的一点P与原点O重合. 让这枚硬币沿数轴的正方向无滑动滚动一周,这时点P转到数轴上点P′的位置 .
(1)线段OP′的长是多少?
(2)在数轴上与点P′,对应的数是哪个数?
探索新知
实际上,图1中小正方形的边长是 ,所以线段OA的长为 ,与点A对应的数是 ;同理,线段OB的长为 ,与点B对应的数是 ;图2中线段OP′的长等于π,与点P′对应的数是π .
由此可知,无理数 , ,π可以用数轴上的点来表示 . 在图1所示的数轴上,按负方向取点A′,使OA′ =OA,则点A对应的数是- .
同理可知,无理数- ,-π也可以用数轴上的点来表示 . 事实上,每个有理数或无理数都可以用数轴上的一个点来表示;反过来,数轴上的点表示的数是有理数或无理数 .
探索新知
结 论
实数和数轴上的点是一一对应(one-to-one correspon-Dence)的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
探索新知
实数与数轴间的关系:
实数与数轴上的点是一一对应的.
它包含着两层含义:
(1)每一个实数都可以用数轴上的一个点来表示;
(2)数轴上的每一个点都表示一个实数.
探索新知
导引:比较一组实数的大小和比较一组有理数的大小一样,可先求出其中无理数的近似数,再将这些数在数轴上表示出来,然后根据“在数轴上右边的点表示的数总比左边的点表示的数大”求解.
解:将各数的大致位置在数轴上表示出来,如图所示.
由图可知,各数用“<”可以连接成:-2 <- <0< <2.5 .
用“<”连接下列各数:- , ,-2 , 2.5 , 0 .
例1
探索新知
总 结
根据“实数与数轴上的点是一一对应的”,并且“在数轴上右边的点表示的数总比左边的点表示的数大”,我们可以利用数形结合思想比较实数的大小.
典题精讲
实数a,b在数轴上的对应点的位置如图所示,把-a,-b,0按照从小到大的顺序排列,正确的是( )
A.-a<0<-b
B.0<-a<-b
C.-b<0<-a
D.0<-b<-a
C
典题精讲
2 和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
A.a<0 B.ab<0
C.aD
D
探索新知
2
知识点
实数的性质
参照有理数的有关概念,谈谈实数的下列概念:
(1) 实数的绝对值 .
(2) 互为相反数的实数 .
(3) —个实数的倒数 .
探索新知
结 论
一个正实数的绝对值是它本身.
一个负实数的绝对值是它的相反数.
0的绝对值是0.
探索新知
在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
(1)相反数:实数a的相反数为-a,若a,b互为相反数,则a+b=0;
(2)非零实数a的倒数为 ,若a,b互为倒数,则ab=1;
(3)绝对值:一个正实数的绝对值是它本身,一个负实数的绝对值是它的相反数,0的绝对值是0.
即:|a|=
探索新知
例2 (1)分别写出- ,π-3.14的相反数;
(2)指出- ,1- 分别是什么数的相反数;
解:(1)因为 ,-(π-3.14) =3.14-π,所以,- ,π-3.14的相反数分别为 , 3.14-π .
(2)因为
所以 分别是 的相反数 .
探索新知
(4)因为
所以绝对值为 的数是 或- .
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数 .
解:(3)因为
所以
典题精讲
1 把下列各数分别填入相应的圈内:
正实数
负实数
有理数
无理数
…
…
…
…
解:正实数:
负实数:
有理数:
无理数:
典题精讲
2 是 的( )
A.相反数 B.倒数
C.负平方根 D.绝对值
3 2- 的绝对值是( )
A.2- B. -2
C.2+ D.±(2- )
A
B
学以致用
小试牛刀
1 . 关于 的叙述,错误的是( )
是有理数 B. 面积为12的正方形边长是
C. 是12的算术平方根 D. 在数轴上可以找到表示 的点
2 . 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A. π-1 B. -π-1
C. -π-1或π-1 D. -π-1或π+1
A
C
小试牛刀
3 . 当a为实数时, =-a,则实数a的数轴上的对应点( ) A.原点的右侧 B.原点的左侧
C.原点或原点的右侧 D.原点或原点的左侧
D
4 . - 的绝对值是( )
A. B. C. - D. 5
C
小试牛刀
5 . 在实数范围内,下列判断正确的是( )
A.若|x|=|y|,则x=y
B.若|x|=( ) ,则x=y
C.若x>y,则x >y
D.若 > ,则x>y
D
小试牛刀
6 . 实数a、b、c在数轴上对应点的位置如图所示,
化简
解:由数轴可知a
所以原式=|a|+(a-b)+c-a+|b-a|
=-a+a-b+c-a+b-a
=c-2a .
课堂小结
课堂小结
1.当数的范围从有理数扩充到实数后,有理数中关于相反数、倒数和绝对值的相关性质同样适用于实数.
2.实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上一个点来表示,反过来数轴上任何一个点都表示一个实数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
