冀教版(新)八上-14.3 实数 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-14.3 实数 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
14.3 实数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
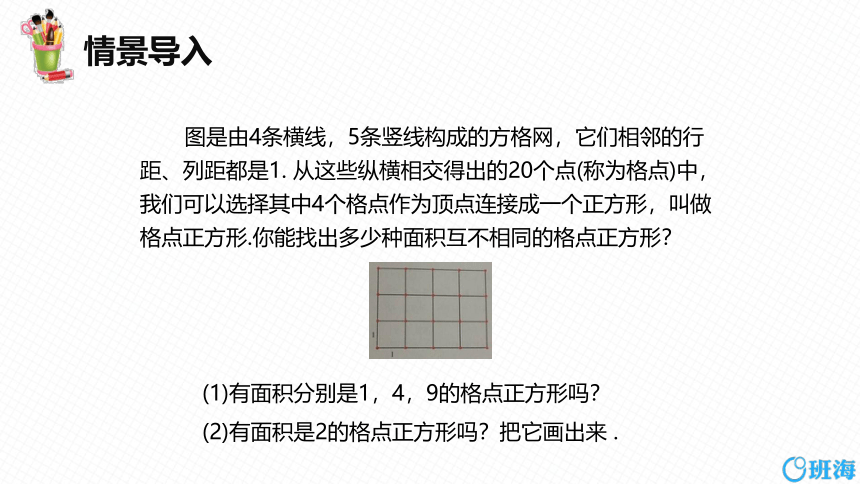
图是由4条横线,5条竖线构成的方格网,它们相邻的行距、列距都是1. 从这些纵横相交得出的20个点(称为格点)中,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.你能找出多少种面积互不相同的格点正方形?
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?把它画出来 .
新课精讲
探索新知
1
知识点
有理数及其局限性
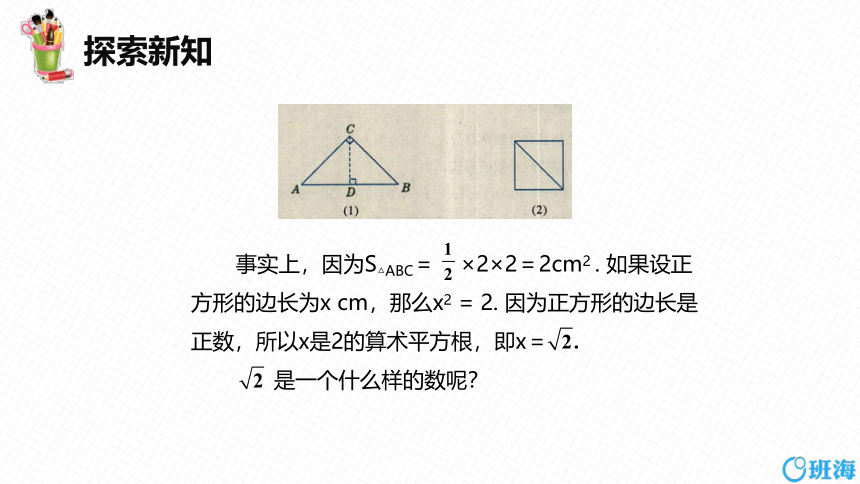
如图(1)所示,在半透明纸上画一个两条直角边都是2 cm的直角三角形ABC,然后剪下这个三角形,再沿斜边上的高CD剪开后,拼成如图(2)所示的正方形 .
(1)这个三角形的面积和拼成的正方形的面积是不是相等?面积是多少?
(2)如果设正方形的边长为x cm,那么x与这个正方形的面积有怎样的关系?
探索新知
事实上,因为S△ABC= ×2×2=2cm2 . 如果设正方形的边长为x cm,那么x2 = 2. 因为正方形的边长是正数,所以x是2的算术平方根,即x=
是一个什么样的数呢?
探索新知
是整数吗?-3,-2,-1,0,1,2,3的平方2吗?你认为有平方后等于2的整数吗?
是分数吗? 的平方等于2吗?你认为有平方后等于2的分数吗?
会是有理数吗?
事实上, 不是有理数 . 借助计算机可以得到
= 1. 414 213 562 373 095 048 801 688 724 209 698 078 569 … .
它是一个无限不循环小数.
我们早就认识的圆周率π,它也是一个无限不循环小数:π
=3. 141 592 653 589 793 238 462 643 383 279 502 884 197 1 ….
问题1
探索新知
有理数包括整数和分数两部分.
(1)整数可以写成小数的形式,如
-10=-10. 0,-1=-1.0, 0=0.0,50=50.0.
对于任意给定的一个整数,你能将它写成小数的形
式吗?
(2)分数可以写成有限小数或无限循环小数,如
=-0.01, =-0.6, =3. 5, =0.187 5,
=-0.333 33…=-0.3, =0. 666 66…=0.6,
问题2
.
.
探索新知
=318 18 …=0.318.
任意给定一个分数,你能将它写成有限小数或无限循环小数的形式吗?(可以借助计算器计算)
(3)有理数是不是总可以写成有限小数或无限循环小数的形式呢?
事实上,有理数总可以写成有限小数或无限循环小数的形式,而 ,π是无限不循环小数.
问题2
.
.
探索新知
结 论
我们把无限不循环小数叫做无理数(irrational number).
其实,无理数有很多,像
=1.732 05…, =2.236 06…, =2.449 48…,
=1.259 92…, =1.442 24…, =2.154 43…,
1. 212 212 221 …(每两个1之间依次多一个2)等,都是无限不循环小数,它们都是无理数.
无理数包括正无理数和负无理数. 如 等,都是正无理数; 等,都是负无理数 .
一般地,如果a是一个正无理数,那么-a是一个负无理数 .
探索新知
下列各数:3.141 59,- ,0.131 131 113…(每两个3之间依次多一个1),-π, ,- 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
B
例1
导引:∵3.141 59是有限小数,∴3.141 59是有理数;
∵- =-2,∴- 是有理数;∵ =5,
∴ 是有理数;∵- 是分数,∴- 是有理数; ∵ 0.131 131 113…(每两个3之间依次多一个1),-π都是无限不循环小数,∴ 0.131 131 113…(每两个3之间依次多一个1),-π是无理数.
探索新知
总 结
(1)对有理数和无理数进行区分时,应先对某些数进行计算或化简,然后根据最后结果进行分类,不能仅看到用根号表示的数就认为是无理数.
(2)π是无理数,化简后含π的数也是无理数.
典题精讲
1 下列说法正确的是( )
A.无限小数都是无理数
B.带根号的数都是无理数
C.无限不循环小数都是无理数
D.无理数都是开方开不尽的数
C
典题精讲
有理数按定义分,它包括______和______;按性质分,它包括____________、0、____________.
3 以下各正方形的边长不是有理数的是( )
A.面积为25的正方形
B.面积为16的正方形
C.面积为8的正方形
D.面积为1.44的正方形
整数
C
分数
正有理数
负有理数
探索新知
2
知识点
实数及其分类
有理数和无理数统称为实数(real number) . 这样,
我们认识的数的范围又一次扩大了,我们可以将实数
按如下方式分类:
探索新知
例2 把下列各数分别填在相应的括号内.
- ,13,-12,+6, ,0,0.8, ,-4.2.
正数:{ ,…};
负数:{ ,…};
正整数:{ ,…};
正分数:{ ,…};
负整数:{ ,…};
负分数:{ ,…}.
13,+6, ,0.8,
- ,-12,-4.2
13,+6
,0.8,
-12
- ,-4.2
探索新知
分析:以前学过的0以外的数就是正数,正数前面加上“-”号就是负数,再看它们是整数还是分数.
点拨:从两个方面看,一是判断正负情况,二是判断是整数还是分数.有限小数和无限循环小数都属于分数.
典题精讲
1 请将下列实数分别填入相应的括号内:
0,2 015,3.144,- ,- ,(-4)3,- , , ,
5.212 112 111 2…(每两个2之间依次多一个1).
有理数:{ …};
无理数:{ …};
整数:{ …};
分数:{ …};
正实数:{ …};
负实数:{ …}.
- ,- ,(-4)3, , ,
.
0, 2 015,3.144,- ,(-4)3, ,
.
5.212 112 111 2…(每两个2之间依次多一个1),
0, 2 015,(-4)3, ,
3.144,- ,
.
2 015,3.144, , 5.212 112 111 2…(每两个2之间依次多一个1),
.
典题精讲
2 把下列各数填入相应的大括号内:
-7,0.32, ,3.14,0, , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), ,- .
有理数:{ ,…};
无理数:{ ,…};
正实数:{ ,…};
实数:{ ,…}.
.
-7,0.32, ,3.14,0
.
, ,0.101 001 000 1…(相邻两个1之间0的个数逐次加1), ,-
0.32, ,3.14, ,0.101 001 000 1…(相邻两
个1之间0的个数逐次加1),
.
-7,0.32, ,3.14,0, , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), ,-
.
典题精讲
3 把下列各数填入相应的圈内(如图):
-|-3|,21.33…,-1.234,- ,0,- ,
- , , , ,1.212 112 111 2…
(相邻两个2之间1的个数依次增加1).
典题精讲
解:
学以致用
小试牛刀
1 . 下列各数中为无理数的是( )
A.-1 B. 3.14 C.π D. 0
C
2 . 下列实数中,是无理数的为( )
A.-4 B . 0. 101 001 C . D.
D
小试牛刀
3 . 在下列各数中是无理数的有:( )
, ,- π, 3.1415, 0.808 008 000 8…
A.2个 B.3个 C.4个 D.5个
B
4 . 下列说法正确的是( )
A.无限小数都是无理数 B.带根号的数都是无理数
C.无理数都是无限小数 D.有理数只是有限小数
C
小试牛刀
5 . 下列实数中属于无理数的是( )
A.3.14 B. C. D.
6 . 下列说法正确的是( )
A.正整数和负整数统称整数 B.0既不是正数,又不是负数
C.0只表示没有 D.正数和负数统称有理数
B
B
小试牛刀
7 . 把下列各数分别填入相应的集合中: -(-230),-2.1, ,0,
-0.99,1.31,5, ,3.14246792…,- .
(1)整数集合:{ …};
(2)负分数集合:{ …};
(3)非正数集合:{ …};
(4)正有理数集合:{ …};
(5)无理数集合: { …}.
-(-230),5,0,
-2.1,-0.99,-
-2.1,-0.99,- ,0,
-(-230), ,1.31,5,
,3.14246792…,
课堂小结
课堂小结
1.无理数的特征:
(1)无理数的小数部分位数无限;
(2)无理数的小数部分不循环,不能表示成分数的形式.
2.常见的无理数的形式:
(1)无限不循环的小数;
(2)特殊字母,如“π”;
(3)an=b(n为大于1的自然数)中b为有理数,则a可能为无理数.
课堂小结
1.实数的概念:有理数和无理数统称为实数.
2.实数的分类:
(1)按定义分类:
课堂小结
(2)按性质分类:
3.易错警示:分类标准不同,分法也就不同,但不管哪种分法都要做到不重不漏;0既不是正实数,也不是负实数.
课堂小结
实数和有理数的绝对值求法相同,都要分为
正数、负数、0来考虑,如下所示:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
14.3 实数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
图是由4条横线,5条竖线构成的方格网,它们相邻的行距、列距都是1. 从这些纵横相交得出的20个点(称为格点)中,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.你能找出多少种面积互不相同的格点正方形?
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?把它画出来 .
新课精讲
探索新知
1
知识点
有理数及其局限性
如图(1)所示,在半透明纸上画一个两条直角边都是2 cm的直角三角形ABC,然后剪下这个三角形,再沿斜边上的高CD剪开后,拼成如图(2)所示的正方形 .
(1)这个三角形的面积和拼成的正方形的面积是不是相等?面积是多少?
(2)如果设正方形的边长为x cm,那么x与这个正方形的面积有怎样的关系?
探索新知
事实上,因为S△ABC= ×2×2=2cm2 . 如果设正方形的边长为x cm,那么x2 = 2. 因为正方形的边长是正数,所以x是2的算术平方根,即x=
是一个什么样的数呢?
探索新知
是整数吗?-3,-2,-1,0,1,2,3的平方2吗?你认为有平方后等于2的整数吗?
是分数吗? 的平方等于2吗?你认为有平方后等于2的分数吗?
会是有理数吗?
事实上, 不是有理数 . 借助计算机可以得到
= 1. 414 213 562 373 095 048 801 688 724 209 698 078 569 … .
它是一个无限不循环小数.
我们早就认识的圆周率π,它也是一个无限不循环小数:π
=3. 141 592 653 589 793 238 462 643 383 279 502 884 197 1 ….
问题1
探索新知
有理数包括整数和分数两部分.
(1)整数可以写成小数的形式,如
-10=-10. 0,-1=-1.0, 0=0.0,50=50.0.
对于任意给定的一个整数,你能将它写成小数的形
式吗?
(2)分数可以写成有限小数或无限循环小数,如
=-0.01, =-0.6, =3. 5, =0.187 5,
=-0.333 33…=-0.3, =0. 666 66…=0.6,
问题2
.
.
探索新知
=318 18 …=0.318.
任意给定一个分数,你能将它写成有限小数或无限循环小数的形式吗?(可以借助计算器计算)
(3)有理数是不是总可以写成有限小数或无限循环小数的形式呢?
事实上,有理数总可以写成有限小数或无限循环小数的形式,而 ,π是无限不循环小数.
问题2
.
.
探索新知
结 论
我们把无限不循环小数叫做无理数(irrational number).
其实,无理数有很多,像
=1.732 05…, =2.236 06…, =2.449 48…,
=1.259 92…, =1.442 24…, =2.154 43…,
1. 212 212 221 …(每两个1之间依次多一个2)等,都是无限不循环小数,它们都是无理数.
无理数包括正无理数和负无理数. 如 等,都是正无理数; 等,都是负无理数 .
一般地,如果a是一个正无理数,那么-a是一个负无理数 .
探索新知
下列各数:3.141 59,- ,0.131 131 113…(每两个3之间依次多一个1),-π, ,- 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
B
例1
导引:∵3.141 59是有限小数,∴3.141 59是有理数;
∵- =-2,∴- 是有理数;∵ =5,
∴ 是有理数;∵- 是分数,∴- 是有理数; ∵ 0.131 131 113…(每两个3之间依次多一个1),-π都是无限不循环小数,∴ 0.131 131 113…(每两个3之间依次多一个1),-π是无理数.
探索新知
总 结
(1)对有理数和无理数进行区分时,应先对某些数进行计算或化简,然后根据最后结果进行分类,不能仅看到用根号表示的数就认为是无理数.
(2)π是无理数,化简后含π的数也是无理数.
典题精讲
1 下列说法正确的是( )
A.无限小数都是无理数
B.带根号的数都是无理数
C.无限不循环小数都是无理数
D.无理数都是开方开不尽的数
C
典题精讲
有理数按定义分,它包括______和______;按性质分,它包括____________、0、____________.
3 以下各正方形的边长不是有理数的是( )
A.面积为25的正方形
B.面积为16的正方形
C.面积为8的正方形
D.面积为1.44的正方形
整数
C
分数
正有理数
负有理数
探索新知
2
知识点
实数及其分类
有理数和无理数统称为实数(real number) . 这样,
我们认识的数的范围又一次扩大了,我们可以将实数
按如下方式分类:
探索新知
例2 把下列各数分别填在相应的括号内.
- ,13,-12,+6, ,0,0.8, ,-4.2.
正数:{ ,…};
负数:{ ,…};
正整数:{ ,…};
正分数:{ ,…};
负整数:{ ,…};
负分数:{ ,…}.
13,+6, ,0.8,
- ,-12,-4.2
13,+6
,0.8,
-12
- ,-4.2
探索新知
分析:以前学过的0以外的数就是正数,正数前面加上“-”号就是负数,再看它们是整数还是分数.
点拨:从两个方面看,一是判断正负情况,二是判断是整数还是分数.有限小数和无限循环小数都属于分数.
典题精讲
1 请将下列实数分别填入相应的括号内:
0,2 015,3.144,- ,- ,(-4)3,- , , ,
5.212 112 111 2…(每两个2之间依次多一个1).
有理数:{ …};
无理数:{ …};
整数:{ …};
分数:{ …};
正实数:{ …};
负实数:{ …}.
- ,- ,(-4)3, , ,
.
0, 2 015,3.144,- ,(-4)3, ,
.
5.212 112 111 2…(每两个2之间依次多一个1),
0, 2 015,(-4)3, ,
3.144,- ,
.
2 015,3.144, , 5.212 112 111 2…(每两个2之间依次多一个1),
.
典题精讲
2 把下列各数填入相应的大括号内:
-7,0.32, ,3.14,0, , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), ,- .
有理数:{ ,…};
无理数:{ ,…};
正实数:{ ,…};
实数:{ ,…}.
.
-7,0.32, ,3.14,0
.
, ,0.101 001 000 1…(相邻两个1之间0的个数逐次加1), ,-
0.32, ,3.14, ,0.101 001 000 1…(相邻两
个1之间0的个数逐次加1),
.
-7,0.32, ,3.14,0, , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), ,-
.
典题精讲
3 把下列各数填入相应的圈内(如图):
-|-3|,21.33…,-1.234,- ,0,- ,
- , , , ,1.212 112 111 2…
(相邻两个2之间1的个数依次增加1).
典题精讲
解:
学以致用
小试牛刀
1 . 下列各数中为无理数的是( )
A.-1 B. 3.14 C.π D. 0
C
2 . 下列实数中,是无理数的为( )
A.-4 B . 0. 101 001 C . D.
D
小试牛刀
3 . 在下列各数中是无理数的有:( )
, ,- π, 3.1415, 0.808 008 000 8…
A.2个 B.3个 C.4个 D.5个
B
4 . 下列说法正确的是( )
A.无限小数都是无理数 B.带根号的数都是无理数
C.无理数都是无限小数 D.有理数只是有限小数
C
小试牛刀
5 . 下列实数中属于无理数的是( )
A.3.14 B. C. D.
6 . 下列说法正确的是( )
A.正整数和负整数统称整数 B.0既不是正数,又不是负数
C.0只表示没有 D.正数和负数统称有理数
B
B
小试牛刀
7 . 把下列各数分别填入相应的集合中: -(-230),-2.1, ,0,
-0.99,1.31,5, ,3.14246792…,- .
(1)整数集合:{ …};
(2)负分数集合:{ …};
(3)非正数集合:{ …};
(4)正有理数集合:{ …};
(5)无理数集合: { …}.
-(-230),5,0,
-2.1,-0.99,-
-2.1,-0.99,- ,0,
-(-230), ,1.31,5,
,3.14246792…,
课堂小结
课堂小结
1.无理数的特征:
(1)无理数的小数部分位数无限;
(2)无理数的小数部分不循环,不能表示成分数的形式.
2.常见的无理数的形式:
(1)无限不循环的小数;
(2)特殊字母,如“π”;
(3)an=b(n为大于1的自然数)中b为有理数,则a可能为无理数.
课堂小结
1.实数的概念:有理数和无理数统称为实数.
2.实数的分类:
(1)按定义分类:
课堂小结
(2)按性质分类:
3.易错警示:分类标准不同,分法也就不同,但不管哪种分法都要做到不重不漏;0既不是正实数,也不是负实数.
课堂小结
实数和有理数的绝对值求法相同,都要分为
正数、负数、0来考虑,如下所示:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
