冀教版(新)八上-15.1 二次根式 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-15.1 二次根式 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:08 | ||
图片预览










文档简介
(共36张PPT)
15.1 二次根式
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
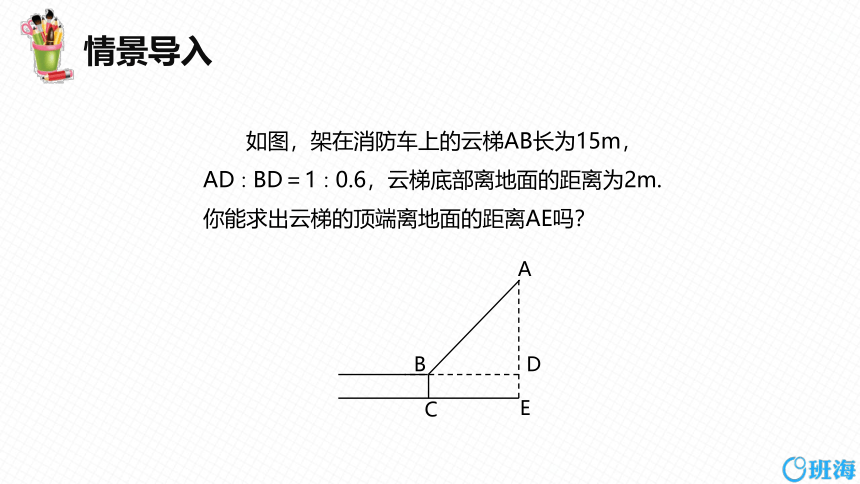
如图,架在消防车上的云梯AB长为15m,AD∶BD=1∶0.6,云梯底部离地面的距离为2m. 你能求出云梯的顶端离地面的距离AE吗?
A
B
C
E
D
情景导入
一艘快艇的航线如下图所示,从O港出发,1小时后回到O港. 若行驶中快艇的速度保持不变. 则快艇驶完AB这段路程用了多少时间
A
B
O
北
东
45°
45°
新课精讲
探索新知
1
知识点
二次根式的定义
1. (1) 2,18, , 的算术平方根是怎样表示的?
(2) 非负数m,p+q,t2-1的算术平方根又是怎样表示的?
探索新知
2. 学校要修建一个占地面积为S m2 的圆形喷水池,它的半径应为多少米? 如果在这个圆形喷水池的外围增加一个占地面积为a m2的环型绿化带,那么所成大圆的半径应为多少米?
探索新知
二次根式:形如 (a≥0)的式子叫做二次根式,其中
“ ”称为二次根号,a称为被开方数.
要点精析:
(1)二次根式的定义是从代数式的结构形式上界定的,
必须含有二次根号“ ”;“ ”的根指数为2,
即 ,“2”一般省略不写.
(2)被开方数a可以是一个数,也可以是一个含有字母的
式子,但前提是a必须大于或等于0.
探索新知
(3)在具体问题中,已知二次根式 ,就意味着给出了a≥0这一条件.
(4)形如 (a≥0)的式子也是二次根式.b与 是相乘的关系,当b为带分数时,要写成假分数的形式.
易错警示:
(1)二次根式是从形式上定义的,不能从化简结果上判断,
如: 等都是二次根式.
(2)像 +1(a≥0)这样的式子只能称为含有二次根式的式子,不能称为二次根式.
探索新知
判断下列各式是否为二次根式,并说明理由.
(1) (2) (3)
(4) +1(a≥0); (5) (6)
判断一个式子是不是二次根式,实质是看它是否具备
二次根式定义的条件,紧扣定义进行识别.
例 1
导引:
探索新知
(1)∵ 的根指数是3,∴ 不是二次根式.
(2)∵不论x为何值,都有x2+1>0,∴ 是二次根式.
(3)当-5a≥0,即a≤0时, 是二次根式;
当a>0时,-5a<0,则 不是二次根式.
∴ 不一定是二次根式.
(4) +1(a≥0)只能称为含有二次根式的代数式,不能称为二次根式.
探索新知
(5)当x=-3时, 无意义,∴ 也无意义;
当x≠-3时, >0,∴ 是二次根式.
∴ 不一定是二次根式.
(6)当a=4,即a-4=0时, 是二次根式;
当a≠4时,-(a-4)2<0,∴ 不是二次根式.
∴ 不一定是二次根式.
探索新知
总 结
二次根式的识别方法:判断一个式子是否为二次根式,一定要紧扣二次根式的定义,看所给的式子是否同时具备二次根式的两个特征:
(1)含根号且根指数为2(通常省略不写);
(2)被开方数为非负数.
典题精讲
1 下列各式中,一定是二次根式的是( )
A. B.
C. D.
D
2 下列式子不一定是二次根式的是( )
A. B. C. D.
A
典题精讲
3 下列式子:
中,一定是二次根式的有( )
A.2个 B.3个
C.4个 D.5个
C
探索新知
2
知识点
二次根式的“双重”非负性
(a≥0) 是一个非负数 .
1.理解二次根式的非负性应从算术平方根入手,当a≥0时, 表示a的算术平方根,因此 ≥0 . 所以“二次根式”包含有两个“非负”即:(1)被开方数非负:a≥0;
(2)二次根式的值非负: ≥0 .
2.若 则 a=0,b=0. 由于二次根式 都是非负数,所以它们的值都为0 .
探索新知
若 则x-y的值为( )
A.1 B.-1 C.7 D.-7
例 2
分析:
据非负数的性质列式求出x、y的值,然后代入代数式
进行计算即可得解.
因为 都是非负数,它们的和
为0,所以
所以y+3=0,x+y-1=0,
解得y=-3,x=4,所以x-y=7. 故选C.
C
探索新知
总 结
两个非负数的和为0时,这两个非负数都为0.
典题精讲
1 若 求a2012+b2012的值.
∵
又∵
∴a+1=0,b-1=0,∴a=-1,b=1,
∴原式=(-1)2012+12012=1+1=2 .
解:
分析:
根据两个非负数的和为0,则这两个非负数都为0,列方程求出a和b的值,再把a和b的值代入所求的代数式中,求出代数式的值 .
2 若 则xy=____.
9
探索新知
3
知识点
二次根式的
1.小亮和小颖对二次根式“ (a≥0)”分别有如下的观点 .
你认同小亮和小颖的观点吗 请举例说明.
2.计算 (a≥0),并与大家交流你的结果 .
小亮的观点
因为 表示的是非负数a的算术平方根,所以,根据算术平方根的意义,有
≥0.
小颖的观点
因为 表示的是非负数a的算术平方根,所以,根据算术平方根和被开方数的关系,有
探索新知
归 纳
事实上,对于二次根式,有
(a≥0)是一个非负数,
=a(a≥0),
=a(a≥0).
探索新知
化简:
(1) (2)
例 3
解:
探索新知
总 结
运用 =a(a≥0), 进行化简的方法:
(1)化简 直接运用 =a(a≥0).
(2)化简 一般有两个步骤:①去掉二次根号,写成绝对值的形式,即 =|a|;②去掉绝对值符号,根据绝对值的意义进行化简,即
典题精讲
1 化简:
(1) (2)
解:
解:
典题精讲
=|x-1|+|x-3|.
∵1≤x<3,∴x-1≥0,x-3<0.
∴原式=x-1-(x-3)=2
解:
解:
典题精讲
2 下列结论正确的是( )
A. B.
C. D.
A
3 若 =1-2a,则( )
A.a> B.a≤
C.a> D.a≥
B
学以致用
小试牛刀
1 . 化简 结果是( )
A. B. C.0 D.无法化简
C
2 . 下列二次根式中: 、 、 、 、 ,最简二次
根式的个数为( )
A.1个 B.2个 C.3个 D.4个
C
小试牛刀
3 . 要使 有意义,a能取的最小整数值为( )
A.0 B.1 C.-1 D.-4
A
4 . 要使式子 有意义,则x的取值范围是( )
A.x>0 B.x≥-2 C.x≥2 D.x≤2
D
小试牛刀
5.下列各式中不是二次根式的是( )
B. C. D.
6.下列式子:
① ;② ;③ ;④ ,
其中二次根式的个数有( )
A.1个 B.2个 C.3个 D.4个
C
B
小试牛刀
7.实数a,b在数轴上对应点的位置如图所示,化简|a|+ 的结果是( )
A.-2a+b B.2a-b
C.-b D.b
A
小试牛刀
8 . 已知a、b为一等腰三角形的两边长,且满足等式
=b-4,求此等腰三角形的周长.
解:根据题意得,3a-6≥0且2-a≥0,
解得a≥2且a≤2,
所以,a=2,b-4=0,解得b=4,
①当腰为2,底为4时不能构成三角形;
②当腰为4,底为2时,周长为4+4+2=10.
故答案为:10.
课堂小结
课堂小结
1. 二次根式的条件:
(1)带二次根号“ ”;(2)被开方数是非负数.
2. 常见具有“非负性”的三类数: (n为正整数);
3. 二次根式的性质:
(1) 中a≥0, ≥0,即一个非负数的算术平方根是一个非负数;
(2) =a(a≥0),即一个非负数的算术平方根的平方等于它本身;
(3) 即一个数的平方的算术平方根等于它的绝对值.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
15.1 二次根式
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,架在消防车上的云梯AB长为15m,AD∶BD=1∶0.6,云梯底部离地面的距离为2m. 你能求出云梯的顶端离地面的距离AE吗?
A
B
C
E
D
情景导入
一艘快艇的航线如下图所示,从O港出发,1小时后回到O港. 若行驶中快艇的速度保持不变. 则快艇驶完AB这段路程用了多少时间
A
B
O
北
东
45°
45°
新课精讲
探索新知
1
知识点
二次根式的定义
1. (1) 2,18, , 的算术平方根是怎样表示的?
(2) 非负数m,p+q,t2-1的算术平方根又是怎样表示的?
探索新知
2. 学校要修建一个占地面积为S m2 的圆形喷水池,它的半径应为多少米? 如果在这个圆形喷水池的外围增加一个占地面积为a m2的环型绿化带,那么所成大圆的半径应为多少米?
探索新知
二次根式:形如 (a≥0)的式子叫做二次根式,其中
“ ”称为二次根号,a称为被开方数.
要点精析:
(1)二次根式的定义是从代数式的结构形式上界定的,
必须含有二次根号“ ”;“ ”的根指数为2,
即 ,“2”一般省略不写.
(2)被开方数a可以是一个数,也可以是一个含有字母的
式子,但前提是a必须大于或等于0.
探索新知
(3)在具体问题中,已知二次根式 ,就意味着给出了a≥0这一条件.
(4)形如 (a≥0)的式子也是二次根式.b与 是相乘的关系,当b为带分数时,要写成假分数的形式.
易错警示:
(1)二次根式是从形式上定义的,不能从化简结果上判断,
如: 等都是二次根式.
(2)像 +1(a≥0)这样的式子只能称为含有二次根式的式子,不能称为二次根式.
探索新知
判断下列各式是否为二次根式,并说明理由.
(1) (2) (3)
(4) +1(a≥0); (5) (6)
判断一个式子是不是二次根式,实质是看它是否具备
二次根式定义的条件,紧扣定义进行识别.
例 1
导引:
探索新知
(1)∵ 的根指数是3,∴ 不是二次根式.
(2)∵不论x为何值,都有x2+1>0,∴ 是二次根式.
(3)当-5a≥0,即a≤0时, 是二次根式;
当a>0时,-5a<0,则 不是二次根式.
∴ 不一定是二次根式.
(4) +1(a≥0)只能称为含有二次根式的代数式,不能称为二次根式.
探索新知
(5)当x=-3时, 无意义,∴ 也无意义;
当x≠-3时, >0,∴ 是二次根式.
∴ 不一定是二次根式.
(6)当a=4,即a-4=0时, 是二次根式;
当a≠4时,-(a-4)2<0,∴ 不是二次根式.
∴ 不一定是二次根式.
探索新知
总 结
二次根式的识别方法:判断一个式子是否为二次根式,一定要紧扣二次根式的定义,看所给的式子是否同时具备二次根式的两个特征:
(1)含根号且根指数为2(通常省略不写);
(2)被开方数为非负数.
典题精讲
1 下列各式中,一定是二次根式的是( )
A. B.
C. D.
D
2 下列式子不一定是二次根式的是( )
A. B. C. D.
A
典题精讲
3 下列式子:
中,一定是二次根式的有( )
A.2个 B.3个
C.4个 D.5个
C
探索新知
2
知识点
二次根式的“双重”非负性
(a≥0) 是一个非负数 .
1.理解二次根式的非负性应从算术平方根入手,当a≥0时, 表示a的算术平方根,因此 ≥0 . 所以“二次根式”包含有两个“非负”即:(1)被开方数非负:a≥0;
(2)二次根式的值非负: ≥0 .
2.若 则 a=0,b=0. 由于二次根式 都是非负数,所以它们的值都为0 .
探索新知
若 则x-y的值为( )
A.1 B.-1 C.7 D.-7
例 2
分析:
据非负数的性质列式求出x、y的值,然后代入代数式
进行计算即可得解.
因为 都是非负数,它们的和
为0,所以
所以y+3=0,x+y-1=0,
解得y=-3,x=4,所以x-y=7. 故选C.
C
探索新知
总 结
两个非负数的和为0时,这两个非负数都为0.
典题精讲
1 若 求a2012+b2012的值.
∵
又∵
∴a+1=0,b-1=0,∴a=-1,b=1,
∴原式=(-1)2012+12012=1+1=2 .
解:
分析:
根据两个非负数的和为0,则这两个非负数都为0,列方程求出a和b的值,再把a和b的值代入所求的代数式中,求出代数式的值 .
2 若 则xy=____.
9
探索新知
3
知识点
二次根式的
1.小亮和小颖对二次根式“ (a≥0)”分别有如下的观点 .
你认同小亮和小颖的观点吗 请举例说明.
2.计算 (a≥0),并与大家交流你的结果 .
小亮的观点
因为 表示的是非负数a的算术平方根,所以,根据算术平方根的意义,有
≥0.
小颖的观点
因为 表示的是非负数a的算术平方根,所以,根据算术平方根和被开方数的关系,有
探索新知
归 纳
事实上,对于二次根式,有
(a≥0)是一个非负数,
=a(a≥0),
=a(a≥0).
探索新知
化简:
(1) (2)
例 3
解:
探索新知
总 结
运用 =a(a≥0), 进行化简的方法:
(1)化简 直接运用 =a(a≥0).
(2)化简 一般有两个步骤:①去掉二次根号,写成绝对值的形式,即 =|a|;②去掉绝对值符号,根据绝对值的意义进行化简,即
典题精讲
1 化简:
(1) (2)
解:
解:
典题精讲
=|x-1|+|x-3|.
∵1≤x<3,∴x-1≥0,x-3<0.
∴原式=x-1-(x-3)=2
解:
解:
典题精讲
2 下列结论正确的是( )
A. B.
C. D.
A
3 若 =1-2a,则( )
A.a> B.a≤
C.a> D.a≥
B
学以致用
小试牛刀
1 . 化简 结果是( )
A. B. C.0 D.无法化简
C
2 . 下列二次根式中: 、 、 、 、 ,最简二次
根式的个数为( )
A.1个 B.2个 C.3个 D.4个
C
小试牛刀
3 . 要使 有意义,a能取的最小整数值为( )
A.0 B.1 C.-1 D.-4
A
4 . 要使式子 有意义,则x的取值范围是( )
A.x>0 B.x≥-2 C.x≥2 D.x≤2
D
小试牛刀
5.下列各式中不是二次根式的是( )
B. C. D.
6.下列式子:
① ;② ;③ ;④ ,
其中二次根式的个数有( )
A.1个 B.2个 C.3个 D.4个
C
B
小试牛刀
7.实数a,b在数轴上对应点的位置如图所示,化简|a|+ 的结果是( )
A.-2a+b B.2a-b
C.-b D.b
A
小试牛刀
8 . 已知a、b为一等腰三角形的两边长,且满足等式
=b-4,求此等腰三角形的周长.
解:根据题意得,3a-6≥0且2-a≥0,
解得a≥2且a≤2,
所以,a=2,b-4=0,解得b=4,
①当腰为2,底为4时不能构成三角形;
②当腰为4,底为2时,周长为4+4+2=10.
故答案为:10.
课堂小结
课堂小结
1. 二次根式的条件:
(1)带二次根号“ ”;(2)被开方数是非负数.
2. 常见具有“非负性”的三类数: (n为正整数);
3. 二次根式的性质:
(1) 中a≥0, ≥0,即一个非负数的算术平方根是一个非负数;
(2) =a(a≥0),即一个非负数的算术平方根的平方等于它本身;
(3) 即一个数的平方的算术平方根等于它的绝对值.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
