冀教版(新)八上-16.3 角的平分线 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-16.3 角的平分线 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
16.3 角的平分线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
小丽用4根两两分别相等的木条订成了一个四边形 . 其中AB=AD,BC=DC . 他的做法是把点A放在角的顶点,AB和AD沿角的两边放下,沿AC画一条射线AE,AE就是角的平分线 . 小丽的做法有道理吗 你能从中悟出什么规律 AC上得点有什么性质吗 你是怎样得到的
新课精讲
探索新知
1
知识点
角平分线的判定
1. 写出角平分线的性质定理的逆命题.
2. 根据这个逆命题的内容,画出图形.
3. 结合图形,提出你对这个逆命题是否正确的猜想.
4. 设法验证你的猜想.
探索新知
归 纳
到角的两边距离相等的点在角平分线上.
探索新知
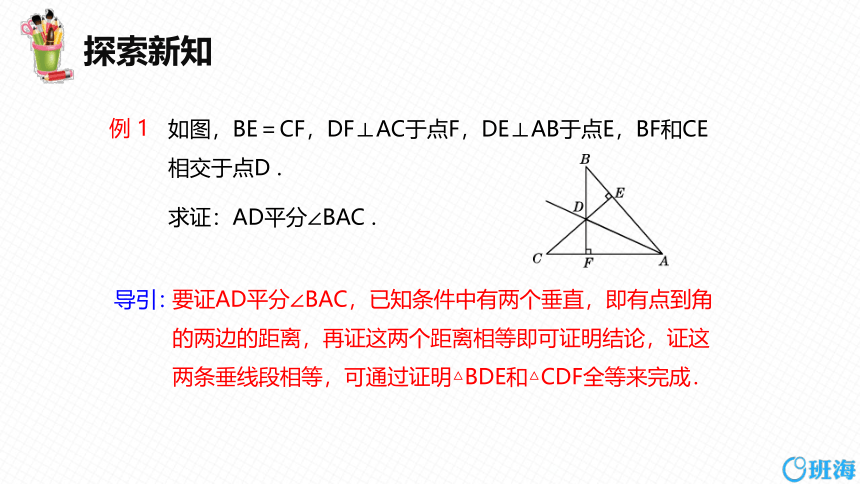
如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D .
求证:AD平分∠BAC .
例 1
要证AD平分∠BAC,已知条件中有两个垂直,即有点到角的两边的距离,再证这两个距离相等即可证明结论,证这两条垂线段相等,可通过证明△BDE和△CDF全等来完成.
导引:
探索新知
∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,∵
∴△BDE≌△CDF(AAS),
∴DE=DF.
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC .
证明:
探索新知
总 结
判定角平分线的两步:
(1)找出角的两边的垂线段;(2)证明两条垂线段相等.
1 在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.点M
B.点N
C.点P
D.点Q
A
典题精讲
典题精讲
2 如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
典题精讲
3 如图,已知AB=AD,CB=CD,连接AC,BD
交于点O.求证:AC⊥BD.
∵AB=AD,∴点A在线段BD的垂直平分线上 .
∵CD=CB,∴点C在线段BD的垂直平分线上 .
∵过两点有且只有一条直线,∴直线AC是线段BD的垂直平分线,
∴AC⊥BD .
证明:
探索新知
2
知识点
三角形的角平分线
如图,AP,CP分别是△ABC的外角∠MAC和∠NCA的平分线,它们交于点P,PD⊥BM于D,PF⊥BN于F . 求证BP为∠MBN的平分线.
例 2
导引:
本题主要考查角平分线的判定方法.本题只要证明出
点P到BM,BN的距离相等即可,而点P是∠MAC与
∠NCA的平分线的交点,故P到AM,AC的距离相等,
到CA,CN的距离也相等,从而可证明PD=PF .
探索新知
证明:
过P作PE⊥AC于点E,如图所示.
∵AP平分∠MAC,PD⊥AM,PE⊥AC,
∴PD=PE,
∵CP平分∠ACN,PF⊥CN,PE⊥AC,
∴PE=PF,∴PD=PF,
∴P在∠MBN的平分线上,
即BP为∠MBN的平分线.
探索新知
总 结
三角形的三条内角平分线相交于一点,三角形的两条外角平分线与一条内角平分线也相交于一点.
1 已知,如图,∠ABC的平分线BD与△ACB的外角平分线
CD相交于点D,连接AD,若∠BDC=40°. 求∠DAC的度数.
典题精讲
解:
因为∠ABC的平分线BD与△ACB的外角平分线CD相交
于点D,所以,点D到直线AB,AC的距离相等,所以
AD是△BAC的外角平分线.
因为∠BDC=180°-∠DBC-∠ACB- (180°-∠ACB)
=180°- ∠ABC-90°- ∠ACB
= (180°-∠ABC-∠ACB)= ∠BAC=40°,所以∠BAC=80°,
2 如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶ S△CAO=_____________.
4∶5∶6
典题精讲
3 到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.以上均不对
B
学以致用
小试牛刀
1 . 如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相
交于点P,若PA=PB,则∠1与∠2的大小是( )
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
A
2 . 如图,△ABC中,∠ABC、∠ACB外角的平分线相交于点F,
连接AF,则下列结论正确的有( )
A.AF平分BC B.AF平分∠BAC
C.AF⊥BC D.以上结论都正确
B
小试牛刀
3 . 如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,
若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A. 有且只有1个
B. 有且只有2个
C. 组成∠E的角平分线
D. 组成∠E的角平分线所在的直线(E点除外)
D
小试牛刀
4 . 已知:如图所示,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=
CD . 求证:D在∠BAC的平分线上 .
解:∵CE⊥AB,BF⊥AC,∴∠BED=∠CFD=90°,
在△BDE和△CDF中,∠BED=∠CFD=90°,∠BDE=∠CDF,BD=CD ,
∴△BDE≌△CDF(AAS). ∴DE=DF .
又∵CE⊥AB,BF⊥AC,∴D在∠BAC的平分线上.
试题分析:首先根据已知条件易证Rt△BDE≌Rt△CDF
(AAS),则DE=DF,再由角平分线性质的逆定理
可得D在∠BAC的平分线上.
小试牛刀
5 . 已知如图所示,PA=PB,∠1+∠2=180°,求证:OP平分∠AOB.
解:证明:∵∠2+∠PBN=180°,∠1+∠2=180°,
∴∠1=∠PBN,过P作PM⊥OA于M,PN⊥OB于N,
则∠PMA=∠PNB=90°,在△PMA和△PNB中,
∴△PMA≌△PNB(AAS),∴PM=PN,
∵PM⊥OA,PN⊥OB,∴OP平分∠AOB.
∠1=∠PBN
∠PMA=∠PNB
PA=PB
课堂小结
课堂小结
角的平分线的性质与判定定理的关系:
1.都与距离有关,即垂直的条件都应具备.
2.点在角的平分线上 点到这个角两边的距离相等.
3.性质反映只要是角的平分线上的点,到角两边的距离就一定相等;判定定理反映只要是到角两边距离相等的点,都应在角的平分线上.
性质
判定定理
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
16.3 角的平分线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
小丽用4根两两分别相等的木条订成了一个四边形 . 其中AB=AD,BC=DC . 他的做法是把点A放在角的顶点,AB和AD沿角的两边放下,沿AC画一条射线AE,AE就是角的平分线 . 小丽的做法有道理吗 你能从中悟出什么规律 AC上得点有什么性质吗 你是怎样得到的
新课精讲
探索新知
1
知识点
角平分线的判定
1. 写出角平分线的性质定理的逆命题.
2. 根据这个逆命题的内容,画出图形.
3. 结合图形,提出你对这个逆命题是否正确的猜想.
4. 设法验证你的猜想.
探索新知
归 纳
到角的两边距离相等的点在角平分线上.
探索新知
如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D .
求证:AD平分∠BAC .
例 1
要证AD平分∠BAC,已知条件中有两个垂直,即有点到角的两边的距离,再证这两个距离相等即可证明结论,证这两条垂线段相等,可通过证明△BDE和△CDF全等来完成.
导引:
探索新知
∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,∵
∴△BDE≌△CDF(AAS),
∴DE=DF.
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC .
证明:
探索新知
总 结
判定角平分线的两步:
(1)找出角的两边的垂线段;(2)证明两条垂线段相等.
1 在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.点M
B.点N
C.点P
D.点Q
A
典题精讲
典题精讲
2 如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
典题精讲
3 如图,已知AB=AD,CB=CD,连接AC,BD
交于点O.求证:AC⊥BD.
∵AB=AD,∴点A在线段BD的垂直平分线上 .
∵CD=CB,∴点C在线段BD的垂直平分线上 .
∵过两点有且只有一条直线,∴直线AC是线段BD的垂直平分线,
∴AC⊥BD .
证明:
探索新知
2
知识点
三角形的角平分线
如图,AP,CP分别是△ABC的外角∠MAC和∠NCA的平分线,它们交于点P,PD⊥BM于D,PF⊥BN于F . 求证BP为∠MBN的平分线.
例 2
导引:
本题主要考查角平分线的判定方法.本题只要证明出
点P到BM,BN的距离相等即可,而点P是∠MAC与
∠NCA的平分线的交点,故P到AM,AC的距离相等,
到CA,CN的距离也相等,从而可证明PD=PF .
探索新知
证明:
过P作PE⊥AC于点E,如图所示.
∵AP平分∠MAC,PD⊥AM,PE⊥AC,
∴PD=PE,
∵CP平分∠ACN,PF⊥CN,PE⊥AC,
∴PE=PF,∴PD=PF,
∴P在∠MBN的平分线上,
即BP为∠MBN的平分线.
探索新知
总 结
三角形的三条内角平分线相交于一点,三角形的两条外角平分线与一条内角平分线也相交于一点.
1 已知,如图,∠ABC的平分线BD与△ACB的外角平分线
CD相交于点D,连接AD,若∠BDC=40°. 求∠DAC的度数.
典题精讲
解:
因为∠ABC的平分线BD与△ACB的外角平分线CD相交
于点D,所以,点D到直线AB,AC的距离相等,所以
AD是△BAC的外角平分线.
因为∠BDC=180°-∠DBC-∠ACB- (180°-∠ACB)
=180°- ∠ABC-90°- ∠ACB
= (180°-∠ABC-∠ACB)= ∠BAC=40°,所以∠BAC=80°,
2 如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶ S△CAO=_____________.
4∶5∶6
典题精讲
3 到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.以上均不对
B
学以致用
小试牛刀
1 . 如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相
交于点P,若PA=PB,则∠1与∠2的大小是( )
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
A
2 . 如图,△ABC中,∠ABC、∠ACB外角的平分线相交于点F,
连接AF,则下列结论正确的有( )
A.AF平分BC B.AF平分∠BAC
C.AF⊥BC D.以上结论都正确
B
小试牛刀
3 . 如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,
若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A. 有且只有1个
B. 有且只有2个
C. 组成∠E的角平分线
D. 组成∠E的角平分线所在的直线(E点除外)
D
小试牛刀
4 . 已知:如图所示,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=
CD . 求证:D在∠BAC的平分线上 .
解:∵CE⊥AB,BF⊥AC,∴∠BED=∠CFD=90°,
在△BDE和△CDF中,∠BED=∠CFD=90°,∠BDE=∠CDF,BD=CD ,
∴△BDE≌△CDF(AAS). ∴DE=DF .
又∵CE⊥AB,BF⊥AC,∴D在∠BAC的平分线上.
试题分析:首先根据已知条件易证Rt△BDE≌Rt△CDF
(AAS),则DE=DF,再由角平分线性质的逆定理
可得D在∠BAC的平分线上.
小试牛刀
5 . 已知如图所示,PA=PB,∠1+∠2=180°,求证:OP平分∠AOB.
解:证明:∵∠2+∠PBN=180°,∠1+∠2=180°,
∴∠1=∠PBN,过P作PM⊥OA于M,PN⊥OB于N,
则∠PMA=∠PNB=90°,在△PMA和△PNB中,
∴△PMA≌△PNB(AAS),∴PM=PN,
∵PM⊥OA,PN⊥OB,∴OP平分∠AOB.
∠1=∠PBN
∠PMA=∠PNB
PA=PB
课堂小结
课堂小结
角的平分线的性质与判定定理的关系:
1.都与距离有关,即垂直的条件都应具备.
2.点在角的平分线上 点到这个角两边的距离相等.
3.性质反映只要是角的平分线上的点,到角两边的距离就一定相等;判定定理反映只要是到角两边距离相等的点,都应在角的平分线上.
性质
判定定理
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
