冀教版(新)八上-17.1 等腰三角形 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-17.1 等腰三角形 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
17.1 等腰三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
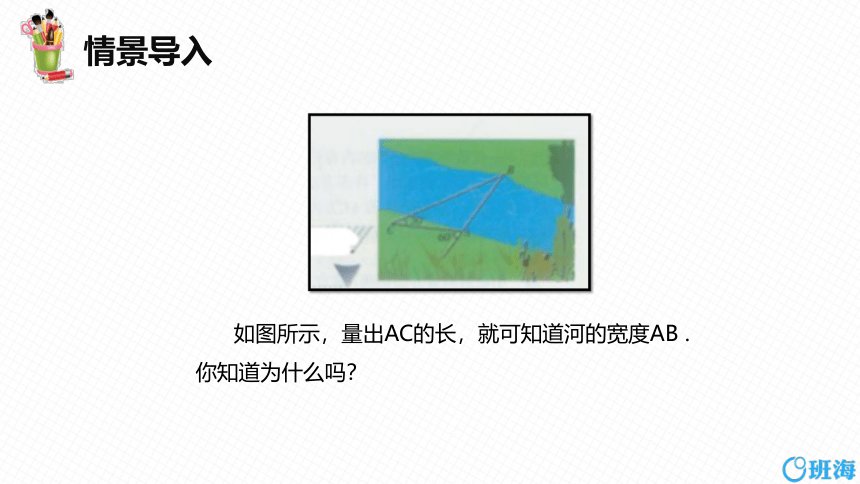
如图所示,量出AC的长,就可知道河的宽度AB .
你知道为什么吗?
新课精讲
探索新知
1
知识点
等腰三角形的判定
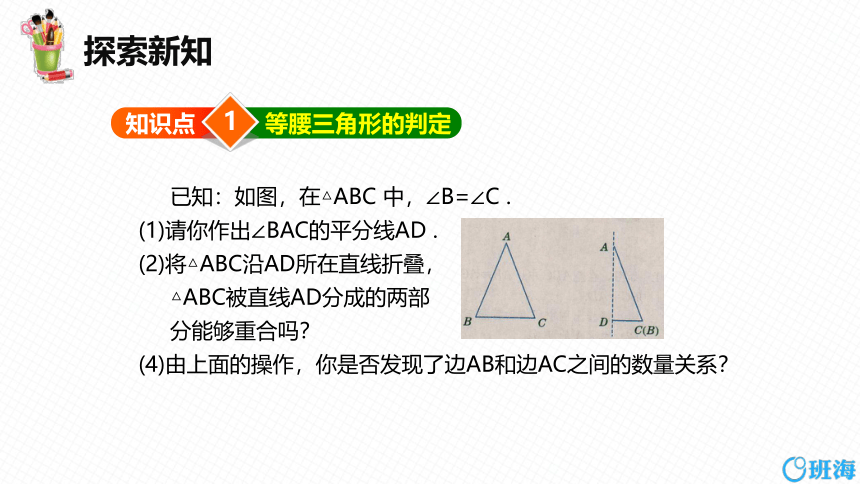
已知:如图,在△ABC 中,∠B=∠C .
(1)请你作出∠BAC的平分线AD .
(2)将△ABC沿AD所在直线折叠,
△ABC被直线AD分成的两部
分能够重合吗?
(4)由上面的操作,你是否发现了边AB和边AC之间的数量关系?
探索新知
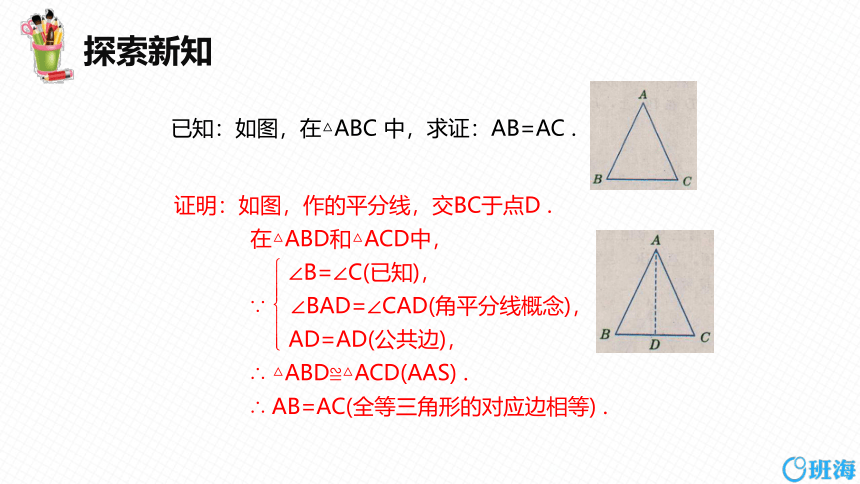
已知:如图,在△ABC 中,求证:AB=AC .
证明:如图,作的平分线,交BC于点D .
在△ABD和△ACD中,
∠B=∠C(已知),
∵ ∠BAD=∠CAD(角平分线概念),
AD=AD(公共边),
∴ △ABD≌△ACD(AAS) .
∴ AB=AC(全等三角形的对应边相等) .
探索新知
归 纳
如果一个三角形有两个角相等,那么这个三角形是等腰三角形. 其中,两个相等的角所对的边相等 . (简称“等角对等边”)
探索新知
导引:要说明△ABC为等腰三角形,由图可知即要说明∠B=∠C,而∠B,∠C分别在两个直角三角形中,因此只要说明∠B,∠C的余角∠BQP,∠R相等即可.
如图,在△ABC中, P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由.
例1
探索新知
解:△ABC是等腰三角形.理由如下:
∵AQ=AR,∴∠R=∠AQR .
又∵∠BQP=∠AQR,∴∠R=∠BQP .
在△QPB和△RPC中,
∠B+∠BQP=180°-∠BPQ=90°,
∠C+∠R=180°-∠CPR=90°,
∴∠B=∠C,
∴AB=AC,即△ABC为等腰三角形.
探索新知
总 结
本题运用了转化思想,将要说明的两等角利用等角的余角相等转化为说明其余角相等;对顶角相等这一隐含条件在推导角的相等关系中起了关键的桥梁作用.根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,就是要证明三角形有两个内角相等.所以证明两个角相等是判定等腰三角形的关键所在.
典题精讲
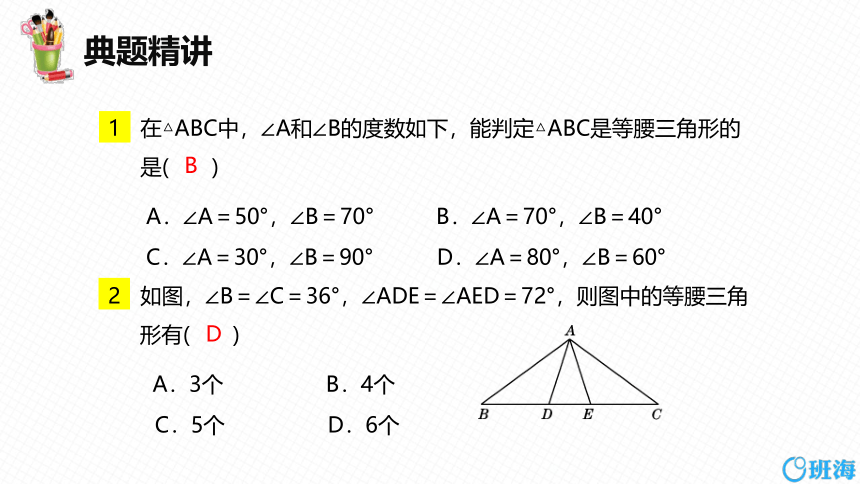
在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角
形有( )
A.3个 B.4个
C.5个 D.6个
B
D
典题精讲
如图,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,给出下列四个条件:
①∠DBO=∠ECO;②∠BDO=∠CEO;
③BD=CE;④OB=OC.
(1)上述四个条件中,哪两个可以判定△ABC是等腰三角形?
(2)选择第(1)题中的一种情形为条件,试说明△ABC是等腰三角形.
解:(1)①③,①④,②③和②④;
(2)以①④为条件,理由:∵OB=OC,∴∠OBC=∠OCB.
又∵∠DBO=∠ECO∴∠DBO+∠OBC=∠ECO+∠OCB,
即∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形.
探索新知
1
知识点
等边三角形的判定
1.三个内角都相等的三角形是等边三角形吗?说出你的理由 .
2.有一个角是60°的等腰三角形一定是等边三角形吗?说出你的理由 .
探索新知
三个角都相等的三角形是等边三角形 .
有一个角等于60°的等腰三角形是等边三角形 .
归 纳
探索新知
例2 如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,
AE∥BC . 证明:△ADE是等边三角形.
导引:由题中条件可证明△ABD≌△ACE,可得AD=AE,又易知∠CAE=60°,因此可以用判定定理2证△ADE是等边三角形.
探索新知
∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=∠BCA=60°,BD⊥AC,
∴∠BDA=90° . ∵AE⊥EC,∴∠CEA=90°,∴∠BDA=∠CEA .
∵AE∥BC,∴∠CAE=∠BCA=60°=∠BAD .
在△ABD和△ACE中,∵
∴△ABD≌△ACE . ∴ AD=AE,又∵∠DAE=60°, ∴△ADE是等边三角形.
证明:
探索新知
证明一个三角形是等边三角形的方法:
(1)若已知三边关系,则选用等边三角形定义来判定;
(2)若已知三角关系,则选用“三个角都相等的三角形是等边三角形”来判定;
(3)若已知是等腰三角形,则选用“有一个角等于60°的等腰三角形是等边三角形”来判定.
总 结
典题精讲
如图,已知点D是等边三角形ABC的边BC延长线上的一点,∠EBC=∠DAC,CE∥AB . 求证:△CDE是等边三角形.
证明:∵△ABC是等边三角形,
∴BC=AC,∠ABC=∠ACB=60° .
∵CE∥AB,∴∠ABC=∠ECD=60°,
∴∠BCE=∠ACD=180°-60°=120° .
在△ACD和△BCE中,∵
∴△ACD≌△BCE,∴CD=CE . ∴△CDE是等边三角形.
典题精讲
2 下列三角形:
①有两个角等于60°的三角形;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
D
典题精讲
如图,∠AOB=120°,OP平分∠AOB,且OP=2 . 若点M,N分
别在OA,OB上,且△PMN为等边三角形,则满足上述条件的
△PMN有( )
A.1个
B.2个
C.3个
D.3个以上
D
学以致用
小试牛刀
1.如果一个三角形有两个角相等,那么这两个角所对的边也________(简
写成“等角对________”).
相等
等边
2.在同一个三角形中,由边________可得出它所对的________相等;反过
来,由角________也能得出它所对的边________.
相等
角
相等
相等
3.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
A.2 B.3
C.4 D.5
D
小试牛刀
4.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形
有( )
A.3个 B.4个
C.5个 D.6个
D
5.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,
将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直
线最多可画( )
A.3条 B.4条 C.5条 D.6条
B
小试牛刀
6.如图,木工师傅从边长为90 cm的正三角形木板上锯出一个正六边形
木板,那么正六边形木板的边长为( )
A.34 cm
B.32 cm
C.30 cm
D.28 cm
C
小试牛刀
7.如图,A,C,B三点在同一条直线上,△DAC和△EBC都是等边三角形,
AE,BD分别与CD,CE交于点M,N.有如下结论:
①△ACE≌△DCB; ②CM=CN; ③AC=DN,
其中正确结论的个数是( )
A.3
B.2
C.1
D.0
B
小试牛刀
8.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的
一点,过点F 作FG⊥BC于G点,并交AB于E点.
求证:(1)AD∥FG;
证明:
∵AB=AC,D是BC的中点,
∴AD⊥BC . 又∵FG⊥BC, ∴ AD∥FG .
小试牛刀
(2)△AFE是等腰三角形.
∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD.
∵AD∥FG,
∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF .
∴AF=AE,即△AEF是等腰三角形.
课堂小结
课堂小结
等腰三角形的三种判定方法
(1)当三角形有两条边相等时,应用“有两条边相等的三角形是等腰三角形”来判定 .
(2)当三角形中有两个角相等时,应用“如果一个三角形有两个角相等,那么这两个角所对的边也相等”来证明 .
(3)当线段垂直平分线上的点与线段两端点构成三角形时,应用“线段垂直平分线上的点到线段两端点的距离相等,则构成的三角形式等腰三角形”来证明 .
课堂小结
根据条件判定等边三角形的解题技巧:
(1)若已知三边关系,则考虑用“三条边都相等的三角形是等边三角形”判定.
(2)若已知三角关系,则根据“三个角都相等的三角形是等边三角形”判定.
(3)若已知该三角形是等腰三角形,则根据“有一个角是60°的等腰三角形是等边三角形”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.1 等腰三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,量出AC的长,就可知道河的宽度AB .
你知道为什么吗?
新课精讲
探索新知
1
知识点
等腰三角形的判定
已知:如图,在△ABC 中,∠B=∠C .
(1)请你作出∠BAC的平分线AD .
(2)将△ABC沿AD所在直线折叠,
△ABC被直线AD分成的两部
分能够重合吗?
(4)由上面的操作,你是否发现了边AB和边AC之间的数量关系?
探索新知
已知:如图,在△ABC 中,求证:AB=AC .
证明:如图,作的平分线,交BC于点D .
在△ABD和△ACD中,
∠B=∠C(已知),
∵ ∠BAD=∠CAD(角平分线概念),
AD=AD(公共边),
∴ △ABD≌△ACD(AAS) .
∴ AB=AC(全等三角形的对应边相等) .
探索新知
归 纳
如果一个三角形有两个角相等,那么这个三角形是等腰三角形. 其中,两个相等的角所对的边相等 . (简称“等角对等边”)
探索新知
导引:要说明△ABC为等腰三角形,由图可知即要说明∠B=∠C,而∠B,∠C分别在两个直角三角形中,因此只要说明∠B,∠C的余角∠BQP,∠R相等即可.
如图,在△ABC中, P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由.
例1
探索新知
解:△ABC是等腰三角形.理由如下:
∵AQ=AR,∴∠R=∠AQR .
又∵∠BQP=∠AQR,∴∠R=∠BQP .
在△QPB和△RPC中,
∠B+∠BQP=180°-∠BPQ=90°,
∠C+∠R=180°-∠CPR=90°,
∴∠B=∠C,
∴AB=AC,即△ABC为等腰三角形.
探索新知
总 结
本题运用了转化思想,将要说明的两等角利用等角的余角相等转化为说明其余角相等;对顶角相等这一隐含条件在推导角的相等关系中起了关键的桥梁作用.根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,就是要证明三角形有两个内角相等.所以证明两个角相等是判定等腰三角形的关键所在.
典题精讲
在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角
形有( )
A.3个 B.4个
C.5个 D.6个
B
D
典题精讲
如图,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,给出下列四个条件:
①∠DBO=∠ECO;②∠BDO=∠CEO;
③BD=CE;④OB=OC.
(1)上述四个条件中,哪两个可以判定△ABC是等腰三角形?
(2)选择第(1)题中的一种情形为条件,试说明△ABC是等腰三角形.
解:(1)①③,①④,②③和②④;
(2)以①④为条件,理由:∵OB=OC,∴∠OBC=∠OCB.
又∵∠DBO=∠ECO∴∠DBO+∠OBC=∠ECO+∠OCB,
即∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形.
探索新知
1
知识点
等边三角形的判定
1.三个内角都相等的三角形是等边三角形吗?说出你的理由 .
2.有一个角是60°的等腰三角形一定是等边三角形吗?说出你的理由 .
探索新知
三个角都相等的三角形是等边三角形 .
有一个角等于60°的等腰三角形是等边三角形 .
归 纳
探索新知
例2 如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,
AE∥BC . 证明:△ADE是等边三角形.
导引:由题中条件可证明△ABD≌△ACE,可得AD=AE,又易知∠CAE=60°,因此可以用判定定理2证△ADE是等边三角形.
探索新知
∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=∠BCA=60°,BD⊥AC,
∴∠BDA=90° . ∵AE⊥EC,∴∠CEA=90°,∴∠BDA=∠CEA .
∵AE∥BC,∴∠CAE=∠BCA=60°=∠BAD .
在△ABD和△ACE中,∵
∴△ABD≌△ACE . ∴ AD=AE,又∵∠DAE=60°, ∴△ADE是等边三角形.
证明:
探索新知
证明一个三角形是等边三角形的方法:
(1)若已知三边关系,则选用等边三角形定义来判定;
(2)若已知三角关系,则选用“三个角都相等的三角形是等边三角形”来判定;
(3)若已知是等腰三角形,则选用“有一个角等于60°的等腰三角形是等边三角形”来判定.
总 结
典题精讲
如图,已知点D是等边三角形ABC的边BC延长线上的一点,∠EBC=∠DAC,CE∥AB . 求证:△CDE是等边三角形.
证明:∵△ABC是等边三角形,
∴BC=AC,∠ABC=∠ACB=60° .
∵CE∥AB,∴∠ABC=∠ECD=60°,
∴∠BCE=∠ACD=180°-60°=120° .
在△ACD和△BCE中,∵
∴△ACD≌△BCE,∴CD=CE . ∴△CDE是等边三角形.
典题精讲
2 下列三角形:
①有两个角等于60°的三角形;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
D
典题精讲
如图,∠AOB=120°,OP平分∠AOB,且OP=2 . 若点M,N分
别在OA,OB上,且△PMN为等边三角形,则满足上述条件的
△PMN有( )
A.1个
B.2个
C.3个
D.3个以上
D
学以致用
小试牛刀
1.如果一个三角形有两个角相等,那么这两个角所对的边也________(简
写成“等角对________”).
相等
等边
2.在同一个三角形中,由边________可得出它所对的________相等;反过
来,由角________也能得出它所对的边________.
相等
角
相等
相等
3.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
A.2 B.3
C.4 D.5
D
小试牛刀
4.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形
有( )
A.3个 B.4个
C.5个 D.6个
D
5.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,
将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直
线最多可画( )
A.3条 B.4条 C.5条 D.6条
B
小试牛刀
6.如图,木工师傅从边长为90 cm的正三角形木板上锯出一个正六边形
木板,那么正六边形木板的边长为( )
A.34 cm
B.32 cm
C.30 cm
D.28 cm
C
小试牛刀
7.如图,A,C,B三点在同一条直线上,△DAC和△EBC都是等边三角形,
AE,BD分别与CD,CE交于点M,N.有如下结论:
①△ACE≌△DCB; ②CM=CN; ③AC=DN,
其中正确结论的个数是( )
A.3
B.2
C.1
D.0
B
小试牛刀
8.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的
一点,过点F 作FG⊥BC于G点,并交AB于E点.
求证:(1)AD∥FG;
证明:
∵AB=AC,D是BC的中点,
∴AD⊥BC . 又∵FG⊥BC, ∴ AD∥FG .
小试牛刀
(2)△AFE是等腰三角形.
∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD.
∵AD∥FG,
∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF .
∴AF=AE,即△AEF是等腰三角形.
课堂小结
课堂小结
等腰三角形的三种判定方法
(1)当三角形有两条边相等时,应用“有两条边相等的三角形是等腰三角形”来判定 .
(2)当三角形中有两个角相等时,应用“如果一个三角形有两个角相等,那么这两个角所对的边也相等”来证明 .
(3)当线段垂直平分线上的点与线段两端点构成三角形时,应用“线段垂直平分线上的点到线段两端点的距离相等,则构成的三角形式等腰三角形”来证明 .
课堂小结
根据条件判定等边三角形的解题技巧:
(1)若已知三边关系,则考虑用“三条边都相等的三角形是等边三角形”判定.
(2)若已知三角关系,则根据“三个角都相等的三角形是等边三角形”判定.
(3)若已知该三角形是等腰三角形,则根据“有一个角是60°的等腰三角形是等边三角形”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
