冀教版(新)八上-17.2 直角三角形【优质课件】
文档属性
| 名称 | 冀教版(新)八上-17.2 直角三角形【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:17 | ||
图片预览










文档简介
(共39张PPT)
17.2 直角三角形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
这幅图画是云南西双版纳傣族干栏房,你能从图中找出形状为直角三角形的部分吗?
新课精讲
探索新知
1
知识点
直角三角形的性质与判定
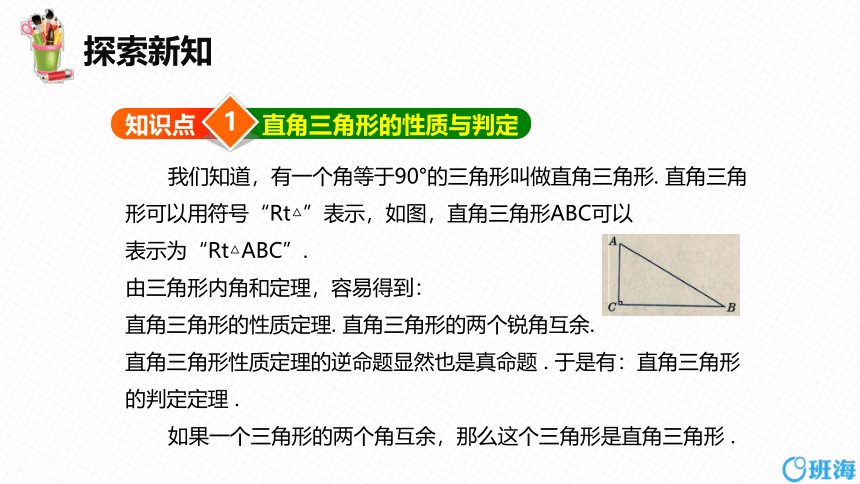
我们知道,有一个角等于90°的三角形叫做直角三角形. 直角三角形可以用符号“Rt△”表示,如图,直角三角形ABC可以
表示为“Rt△ABC”.
由三角形内角和定理,容易得到:
直角三角形的性质定理. 直角三角形的两个锐角互余.
直角三角形性质定理的逆命题显然也是真命题 . 于是有:直角三角形的判定定理 .
如果一个三角形的两个角互余,那么这个三角形是直角三角形 .
探索新知
“直角三角形的两个锐角互余”及“有两个角互余的三角形是直角三角形”都可以利用三角形的内角和定理推出.
(2)在直角三角形中,若已知两个锐角之间的关系,结合两锐角互余可以求出每个锐角的度数,而不必再使用三角形内角和定理求解.
(3)在判定一个三角形是直角三角形时,除利用直角三角形的定义外,还可找出有两个锐角互余,从而直接判定直角三角形.
探索新知
如图,已知∠A=32°,∠ADC=110°,BE⊥AC于点E,求∠B的度数.
例1
解:∵∠A=32°,∠ADC=110°,∴∠C=180°-32°-110°=38°.
又∵BE⊥AC,∴△BEC为直角三角形,
∴∠B=90°-∠C=90°-38°=52°(直角三角形的两个锐角互余).
点拨:直角三角形是特殊的三角形,在直角三角形中,可以利用直角三角形的两个锐角互余求角的度数的问题,也可以利用三角形内角和定理来求解.
探索新知
总 结
直角三角形是特殊的三角形,直角三角形的两锐角互余的本质是三角形内角和定理,是三角形内角和定理的一种简化应用,利用这一性质,在直角三角形中已知一锐角可求另一锐角.
典题精讲
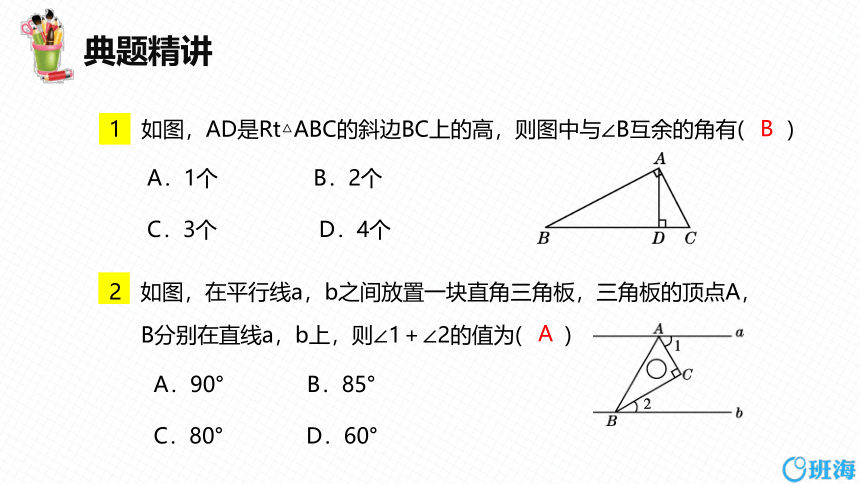
如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个
C.3个 D.4个
2 如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,
B分别在直线a,b上,则∠1+∠2的值为( )
A.90° B.85°
C.80° D.60°
B
A
探索新知
例2 如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平
分线与∠DFE的平分线相交于点P . 试说明△EFP为直角三角形.
导引:判定△EFP为直角三角形,有两种方法:①有一角是直角,②两锐角互余,即要说明∠EPF=90°或∠EFP+∠FEP=90°.
∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE .
∴∠PEF+∠PFE= (∠BEF+∠DFE)= ×180°=90° . ∴ △EFP为直角三角形.
解:
探索新知
根据直角三角形的定义可以判定直角三角形;由直角三角形的判定定理也可判定直角三角形.有两个角互余,由三角形内角和定理可知第三个角是直角,因此它的实质还是直角三角形的定义.
总 结
典题精讲
如图,BD平分∠ABC,∠ADB=60°,∠BDC=80°,∠C=70°. 试判断△ABD的形状.
解:在△DBC中,∠DBC=180°-∠BDC-∠C=
180°-80°-70°=30°.
∵BD平分∠ABC,∴∠ABD=∠DBC=30°.
在△ABD中,
∵∠ADB+∠ABD=60°+30°=90°,
∴△ABD是直角三角形.
典题精讲
如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数
为( )
A.50° B.45° C.40° D.30°
C
探索新知
2
知识点
直角三角形斜边上的中线性质
在一张半透明的纸上画出Rt△ABC,∠C=90°,如图(1);将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE, 如图(2);将纸展开,如图(3) .
探索新知
(1)∠ECF与∠B有怎样的关系?线段EC与线段EB有怎样的关系?
(2)由发现的上述关系以及∠A+∠B=∠ACB,∠ACE+∠ECF=∠ACB,你能判断∠ACE与∠A的大小关系吗?线段AE与线段CE呢?从而你发现了什么结论?将你的结论与大家交流 .
我们发现,CE=AE=EB,即CE是AB的中线,且CE= AB .
下面就来证明上面的“发现”.
探索新知
已知:如图,在 Rt△ABC 中,∠ACB= 90°, CD为斜边AB上的中线 .
求证:CD= AB .
证明:如图,过点D,作DE∥BC,交AC于 点E;作DF∥AC,交BC于点F .
在△AED 和△DFB 中,
∠A=∠FDB(两直线平行,同位角相等),
∵ AD=DB(中线的概念),
∠ADE=∠B(两直线平行,同位角相等),
探索新知
∴△AED≌△DFB (ASA) .
∴QE=DF,ED=FB . (全等三角形的对应边相等)
同理可证,△CDE≌△DCF .
从而,ED=FC,EC=FD .
∴ AE=EC,CF=FB . (等量代换)
又∵DE⊥AC,DF⊥BC,(两直线平行,同位角相等)
∴DE为AC的垂直平分线,DF为BC的垂直平分线 .
∴AD=CD=BD(线段垂直平分线的性质定理) .
CD= AB .
探索新知
直角三角形斜边上的中线等于斜边的一半 .
归 纳
探索新知
例3 如图,BD,CE是△ABC的两条高,M,N分别是BC,DE的中
点.求证:MN⊥DE .
导引:如图,连接EM,DM,由CE与BD为△ABC的
两条高,可得△BEC与△BDC均为直角三角形,根据M
为BC的中点,利用“直角三角形斜边上的中线等于斜边的一半”可得EM为BC的一半,DM也为BC的一半,通过等量代换可得EM=DM,又因为N为DE的中点,所以MN⊥DE .
探索新知
连接EM,DM,如图 .
∵CE,BD为△ABC的两条高,
∴CE⊥AB,BD⊥AC,
∴∠BEC=∠BDC=90° .
在Rt△BEC中,M为斜边BC的中点,
∴EM= BC .
在Rt△BDC中,M为斜边BC的中点,
∴DM= BC . ∴EM=DM .
又∵N为DE的中点,∴MN⊥DE .
证明:
探索新知
若题目中出现了一边的中点,往往需要用到中线,若又有直角,往往需要用到直角三角形斜边上的中线等于斜边的一半.
总 结
典题精讲
如图,在四边形ABCD中,∠DAB=∠DCB=90°,AC与BD相交于点O,M,N分别是BD,AC的中点.求证:MN⊥AC .
证明:连接AM,MC .
在△DCB和△BAD中,
∠DCB=∠DAB=90°,
∴△DCB和△BAD均为直角三角形.
∵M是BD的中点,
∴MC= BD,AM= BD . ∴MC= AM .
又∵N是AC的中点,∴MN⊥AC .
典题精讲
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
如图,在Rt△ACB中,∠ACB=90°,CD为AB边上的中线,∠A=
30°. 若CD=6,则BC的长度为( )
A.2 B.4
C.6 D.8
C
D
探索新知
3
知识点
含30°角的直角三角形的性质
证明:在直角三角形中,30°角所对的直角边等于斜边的一半 .
1.性质:在直角三角形中,30°角所对的直角边等于斜边的一半.
要点精析:(1)适用条件——含30°角的直角三角形.
(2)揭示的关系——30°角所对的直角边与斜边的关系.
拓展:在直角三角形中,若一直角边等于斜边的一半,则该直角边所对的角为30°.
2.作用:应用于证线段的倍数关系和计算角度.
探索新知
例4 如图17.2 6,在等边三角形ABC中,点D,E分别在边BC,AC
上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F .
(1)求∠F的度数;
(2)若CD=2,求DF的长.
导引:(1)根据平行线的性质可得∠EDC=∠B=60°,再根据三角形内角和定理即可求解;
(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
探索新知
(1)∵△ABC是等边三角形,∴∠B=60° .
∵DE∥AB,∴∠EDC=∠B=60° .
∵EF⊥DE,∴∠DEF=90° .
∴∠F=90°-∠EDC=30° .
(2)∵∠ACB=60°,∠EDC=60°,
∴∠DEC=60° . ∴∠ACB=∠EDC=∠DEC .
∴△EDC是等边三角形.∴DE=CD=2 .
∵∠DEF=90°,∠F=30°,
∴DF=2DE=4 .
解:
探索新知
利用含30°角的直角三角形的性质,关键有两个元素:一是30°的角;二是直角三角形.根据这两个元素可建立直角三角形中斜边与一条直角边之间的关系.
总 结
典题精讲
如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )
A.1 B.2
C.4 D.8
B
如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直
平分线ED交 AB于点E,交BC于点D,若CD=3,则
BD的长为_____.
6
典题精讲
在Rt△ABC中,∠A=30°,则下列结论正确的是( )
A.BC= AB
B.BC≠ AB
C.当∠B=90°时,BC= AB
D.当∠C=90°时,BC= AB
D
学以致用
小试牛刀
1 . 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中
点,DE=5,BC=8,则△DEF的周长是( )
A . 21 B . 18
C . 13 D . 15
C
2 . 如图,在△ABC中,∠BAC=90°,∠C=30°,D为BC的中点,AE
⊥BC,垂足为E,连接AD,则AB与DE的大小关系是( )
A . 3AB=4DE B . 2AB=3DE
C . AB=2DE D . AB=3DE
C
小试牛刀
3 . 如图是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=10m,∠A=30°,则立柱BC的长度是( )
A . 5m B . 8m
C . 10m D . 20m
A
4 . 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,
点D为BC的中点,AE⊥Bc,垂足为E,连接AD,
则图中与AD相等的线段有( )
A . 1条 B . 2条 C . 3条 D . 4条
C
小试牛刀
5 . 如图,在△ABC中,∠C为直角,∠A=30°,CD⊥AB于D,
若BD=2,则AB的长为( )
A.8 B.6 C.4 D.2
A
6 . 如图所示,在△ABC中,CD,BE是两条高,那么图中与∠A相等
的角的个数有( )
A.1个 B.2个 C.3个 D.4个
B
小试牛刀
7 . 如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
解:(1)∵∠ACB=90°,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B .
(2)在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,
又∵∠CEF=∠AED,∴∠CEF=∠CFE.
小试牛刀
8 . 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,
BQ⊥AD于Q,PQ=3,PE=1,∠PBQ=30°,求AD的长.
解:∵等边△ABC
∴AB=AC,∠BAC=∠C=60
∵AE=CD
∴△ABE≌△CAD (SAS) ∴AD=BE ∵BQ⊥AD, ∠PBQ=30°
∴BP=2PQ=6 ∴ BE=BP+PE=6+1=7 ∴ AD=7
课堂小结
课堂小结
在直角三角形中,30°角所对的直角边等于斜边的一半.这个定理将特殊的直角三角形中的角度关系转化为直角三角形中边的等量关系.在一般情况下,遇到30°角常用的添加辅助线的方法就是作垂直,构造含30°角的直角三角形,解决相关的线段问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.2 直角三角形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
这幅图画是云南西双版纳傣族干栏房,你能从图中找出形状为直角三角形的部分吗?
新课精讲
探索新知
1
知识点
直角三角形的性质与判定
我们知道,有一个角等于90°的三角形叫做直角三角形. 直角三角形可以用符号“Rt△”表示,如图,直角三角形ABC可以
表示为“Rt△ABC”.
由三角形内角和定理,容易得到:
直角三角形的性质定理. 直角三角形的两个锐角互余.
直角三角形性质定理的逆命题显然也是真命题 . 于是有:直角三角形的判定定理 .
如果一个三角形的两个角互余,那么这个三角形是直角三角形 .
探索新知
“直角三角形的两个锐角互余”及“有两个角互余的三角形是直角三角形”都可以利用三角形的内角和定理推出.
(2)在直角三角形中,若已知两个锐角之间的关系,结合两锐角互余可以求出每个锐角的度数,而不必再使用三角形内角和定理求解.
(3)在判定一个三角形是直角三角形时,除利用直角三角形的定义外,还可找出有两个锐角互余,从而直接判定直角三角形.
探索新知
如图,已知∠A=32°,∠ADC=110°,BE⊥AC于点E,求∠B的度数.
例1
解:∵∠A=32°,∠ADC=110°,∴∠C=180°-32°-110°=38°.
又∵BE⊥AC,∴△BEC为直角三角形,
∴∠B=90°-∠C=90°-38°=52°(直角三角形的两个锐角互余).
点拨:直角三角形是特殊的三角形,在直角三角形中,可以利用直角三角形的两个锐角互余求角的度数的问题,也可以利用三角形内角和定理来求解.
探索新知
总 结
直角三角形是特殊的三角形,直角三角形的两锐角互余的本质是三角形内角和定理,是三角形内角和定理的一种简化应用,利用这一性质,在直角三角形中已知一锐角可求另一锐角.
典题精讲
如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个
C.3个 D.4个
2 如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,
B分别在直线a,b上,则∠1+∠2的值为( )
A.90° B.85°
C.80° D.60°
B
A
探索新知
例2 如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平
分线与∠DFE的平分线相交于点P . 试说明△EFP为直角三角形.
导引:判定△EFP为直角三角形,有两种方法:①有一角是直角,②两锐角互余,即要说明∠EPF=90°或∠EFP+∠FEP=90°.
∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE .
∴∠PEF+∠PFE= (∠BEF+∠DFE)= ×180°=90° . ∴ △EFP为直角三角形.
解:
探索新知
根据直角三角形的定义可以判定直角三角形;由直角三角形的判定定理也可判定直角三角形.有两个角互余,由三角形内角和定理可知第三个角是直角,因此它的实质还是直角三角形的定义.
总 结
典题精讲
如图,BD平分∠ABC,∠ADB=60°,∠BDC=80°,∠C=70°. 试判断△ABD的形状.
解:在△DBC中,∠DBC=180°-∠BDC-∠C=
180°-80°-70°=30°.
∵BD平分∠ABC,∴∠ABD=∠DBC=30°.
在△ABD中,
∵∠ADB+∠ABD=60°+30°=90°,
∴△ABD是直角三角形.
典题精讲
如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数
为( )
A.50° B.45° C.40° D.30°
C
探索新知
2
知识点
直角三角形斜边上的中线性质
在一张半透明的纸上画出Rt△ABC,∠C=90°,如图(1);将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE, 如图(2);将纸展开,如图(3) .
探索新知
(1)∠ECF与∠B有怎样的关系?线段EC与线段EB有怎样的关系?
(2)由发现的上述关系以及∠A+∠B=∠ACB,∠ACE+∠ECF=∠ACB,你能判断∠ACE与∠A的大小关系吗?线段AE与线段CE呢?从而你发现了什么结论?将你的结论与大家交流 .
我们发现,CE=AE=EB,即CE是AB的中线,且CE= AB .
下面就来证明上面的“发现”.
探索新知
已知:如图,在 Rt△ABC 中,∠ACB= 90°, CD为斜边AB上的中线 .
求证:CD= AB .
证明:如图,过点D,作DE∥BC,交AC于 点E;作DF∥AC,交BC于点F .
在△AED 和△DFB 中,
∠A=∠FDB(两直线平行,同位角相等),
∵ AD=DB(中线的概念),
∠ADE=∠B(两直线平行,同位角相等),
探索新知
∴△AED≌△DFB (ASA) .
∴QE=DF,ED=FB . (全等三角形的对应边相等)
同理可证,△CDE≌△DCF .
从而,ED=FC,EC=FD .
∴ AE=EC,CF=FB . (等量代换)
又∵DE⊥AC,DF⊥BC,(两直线平行,同位角相等)
∴DE为AC的垂直平分线,DF为BC的垂直平分线 .
∴AD=CD=BD(线段垂直平分线的性质定理) .
CD= AB .
探索新知
直角三角形斜边上的中线等于斜边的一半 .
归 纳
探索新知
例3 如图,BD,CE是△ABC的两条高,M,N分别是BC,DE的中
点.求证:MN⊥DE .
导引:如图,连接EM,DM,由CE与BD为△ABC的
两条高,可得△BEC与△BDC均为直角三角形,根据M
为BC的中点,利用“直角三角形斜边上的中线等于斜边的一半”可得EM为BC的一半,DM也为BC的一半,通过等量代换可得EM=DM,又因为N为DE的中点,所以MN⊥DE .
探索新知
连接EM,DM,如图 .
∵CE,BD为△ABC的两条高,
∴CE⊥AB,BD⊥AC,
∴∠BEC=∠BDC=90° .
在Rt△BEC中,M为斜边BC的中点,
∴EM= BC .
在Rt△BDC中,M为斜边BC的中点,
∴DM= BC . ∴EM=DM .
又∵N为DE的中点,∴MN⊥DE .
证明:
探索新知
若题目中出现了一边的中点,往往需要用到中线,若又有直角,往往需要用到直角三角形斜边上的中线等于斜边的一半.
总 结
典题精讲
如图,在四边形ABCD中,∠DAB=∠DCB=90°,AC与BD相交于点O,M,N分别是BD,AC的中点.求证:MN⊥AC .
证明:连接AM,MC .
在△DCB和△BAD中,
∠DCB=∠DAB=90°,
∴△DCB和△BAD均为直角三角形.
∵M是BD的中点,
∴MC= BD,AM= BD . ∴MC= AM .
又∵N是AC的中点,∴MN⊥AC .
典题精讲
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
如图,在Rt△ACB中,∠ACB=90°,CD为AB边上的中线,∠A=
30°. 若CD=6,则BC的长度为( )
A.2 B.4
C.6 D.8
C
D
探索新知
3
知识点
含30°角的直角三角形的性质
证明:在直角三角形中,30°角所对的直角边等于斜边的一半 .
1.性质:在直角三角形中,30°角所对的直角边等于斜边的一半.
要点精析:(1)适用条件——含30°角的直角三角形.
(2)揭示的关系——30°角所对的直角边与斜边的关系.
拓展:在直角三角形中,若一直角边等于斜边的一半,则该直角边所对的角为30°.
2.作用:应用于证线段的倍数关系和计算角度.
探索新知
例4 如图17.2 6,在等边三角形ABC中,点D,E分别在边BC,AC
上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F .
(1)求∠F的度数;
(2)若CD=2,求DF的长.
导引:(1)根据平行线的性质可得∠EDC=∠B=60°,再根据三角形内角和定理即可求解;
(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
探索新知
(1)∵△ABC是等边三角形,∴∠B=60° .
∵DE∥AB,∴∠EDC=∠B=60° .
∵EF⊥DE,∴∠DEF=90° .
∴∠F=90°-∠EDC=30° .
(2)∵∠ACB=60°,∠EDC=60°,
∴∠DEC=60° . ∴∠ACB=∠EDC=∠DEC .
∴△EDC是等边三角形.∴DE=CD=2 .
∵∠DEF=90°,∠F=30°,
∴DF=2DE=4 .
解:
探索新知
利用含30°角的直角三角形的性质,关键有两个元素:一是30°的角;二是直角三角形.根据这两个元素可建立直角三角形中斜边与一条直角边之间的关系.
总 结
典题精讲
如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )
A.1 B.2
C.4 D.8
B
如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直
平分线ED交 AB于点E,交BC于点D,若CD=3,则
BD的长为_____.
6
典题精讲
在Rt△ABC中,∠A=30°,则下列结论正确的是( )
A.BC= AB
B.BC≠ AB
C.当∠B=90°时,BC= AB
D.当∠C=90°时,BC= AB
D
学以致用
小试牛刀
1 . 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中
点,DE=5,BC=8,则△DEF的周长是( )
A . 21 B . 18
C . 13 D . 15
C
2 . 如图,在△ABC中,∠BAC=90°,∠C=30°,D为BC的中点,AE
⊥BC,垂足为E,连接AD,则AB与DE的大小关系是( )
A . 3AB=4DE B . 2AB=3DE
C . AB=2DE D . AB=3DE
C
小试牛刀
3 . 如图是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=10m,∠A=30°,则立柱BC的长度是( )
A . 5m B . 8m
C . 10m D . 20m
A
4 . 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,
点D为BC的中点,AE⊥Bc,垂足为E,连接AD,
则图中与AD相等的线段有( )
A . 1条 B . 2条 C . 3条 D . 4条
C
小试牛刀
5 . 如图,在△ABC中,∠C为直角,∠A=30°,CD⊥AB于D,
若BD=2,则AB的长为( )
A.8 B.6 C.4 D.2
A
6 . 如图所示,在△ABC中,CD,BE是两条高,那么图中与∠A相等
的角的个数有( )
A.1个 B.2个 C.3个 D.4个
B
小试牛刀
7 . 如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
解:(1)∵∠ACB=90°,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B .
(2)在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,
又∵∠CEF=∠AED,∴∠CEF=∠CFE.
小试牛刀
8 . 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,
BQ⊥AD于Q,PQ=3,PE=1,∠PBQ=30°,求AD的长.
解:∵等边△ABC
∴AB=AC,∠BAC=∠C=60
∵AE=CD
∴△ABE≌△CAD (SAS) ∴AD=BE ∵BQ⊥AD, ∠PBQ=30°
∴BP=2PQ=6 ∴ BE=BP+PE=6+1=7 ∴ AD=7
课堂小结
课堂小结
在直角三角形中,30°角所对的直角边等于斜边的一半.这个定理将特殊的直角三角形中的角度关系转化为直角三角形中边的等量关系.在一般情况下,遇到30°角常用的添加辅助线的方法就是作垂直,构造含30°角的直角三角形,解决相关的线段问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
