冀教版(新)八上-17.3 勾股定理 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-17.3 勾股定理 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:17 | ||
图片预览








文档简介
(共33张PPT)
17.3 勾股定理
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
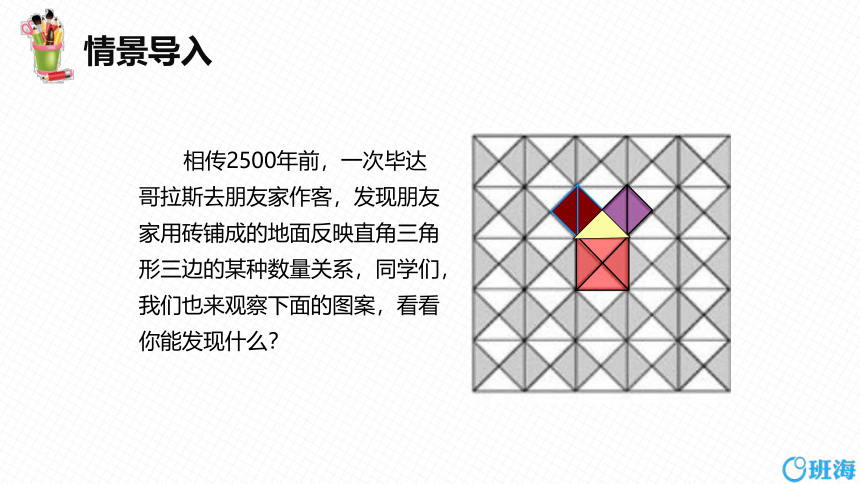
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
新课精讲
探索新知
1
知识点
勾股定理的实际应用
1.勾股定理的数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,则a2+b2=c2 .
要点精析:
(1)勾股定理适用于任何一个直角三角形;
(2)勾股定理的内容描述的是直角三角形三边之间的数量关系,已知其中任意两边可以求出第三边;
(3)勾股定理的变形公式:a2=c2-b2,b2=c2-a2;
(4)运用勾股定理时,要分清斜边、直角边.
探索新知
2. 基本思想方法:
勾股定理把“形”与“数”有机地结合起来,即把直角三角形这个“形”与三边关系这一“数”结合起来,它是数形结合思想的典范.
易错警示:运用勾股定理时,一定要分清哪条边是斜边 . 在不清楚哪条边是斜边时,要分类讨论,写出所有可能,以免漏解或错解.
探索新知
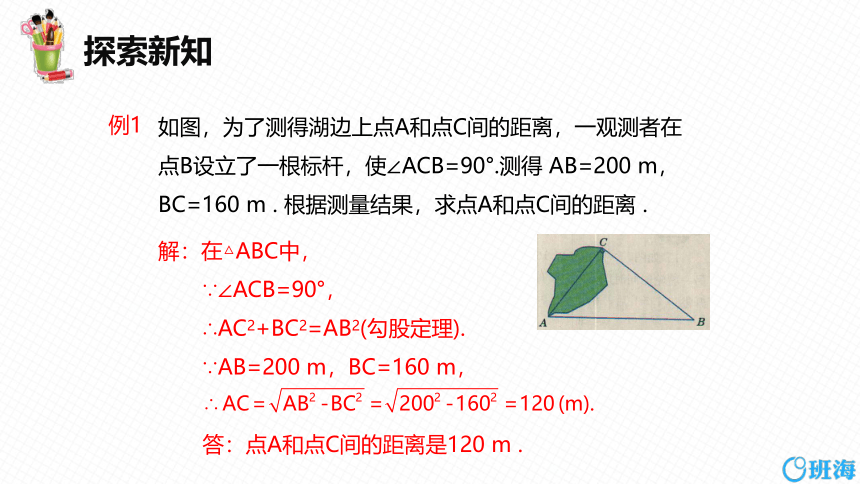
如图,为了测得湖边上点A和点C间的距离,一观测者在点B设立了一根标杆,使∠ACB=90°.测得 AB=200 m,BC=160 m . 根据测量结果,求点A和点C间的距离 .
例1
解:在△ABC中,
∵∠ACB=90°,
∴AC2+BC2=AB2(勾股定理).
∵AB=200 m,BC=160 m,
答:点A和点C间的距离是120 m .
探索新知
总 结
解决这类实际问题的关键是根据题意,画出图形,建立数学模型,用数学知识解答,把复杂问题简单化、明朗化 .
典题精讲
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在的位置B处与灯塔P之间的距离为( )
A.60 海里
B.45 海里
C.20 海里
D.30 海里
D
典题精讲
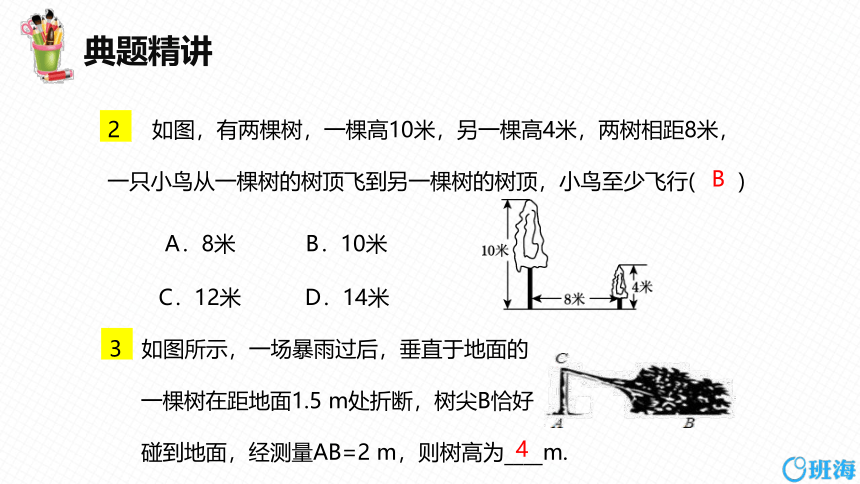
2 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8米 B.10米
C.12米 D.14米
B
如图所示,一场暴雨过后,垂直于地面的
一棵树在距地面1.5 m处折断,树尖B恰好
碰到地面,经测量AB=2 m,则树高为____m.
4
探索新知
2
知识点
勾股定理的几何应用
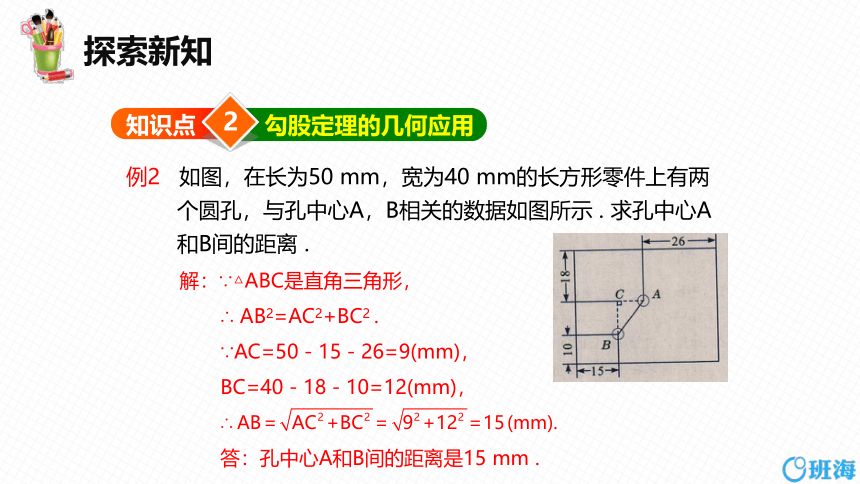
例2 如图,在长为50 mm,宽为40 mm的长方形零件上有两
个圆孔,与孔中心A,B相关的数据如图所示 . 求孔中心A
和B间的距离 .
解:∵△ABC是直角三角形,
∴ AB2=AC2+BC2 .
∵AC=50-15-26=9(mm),
BC=40-18-10=12(mm),
答:孔中心A和B间的距离是15 mm .
探索新知
利用勾股定理求未知边长时,关键要找准斜边,找斜边,就是找直角,直角所对的边就是斜边.
总 结
典题精讲
如图,在△ABC中,AB=AC=12,BC=16 . 求△ABC的面积 .
解:过点A作AD⊥BC,交BC于点D .
∵AB=AC,∴AD是△ABC底边BC上的中线,
∴BD=CD= BC= ×16=8 .
在Rt△ABD中,由勾股定理,得AD2=AB2-BD2=122-82,AD=4 .
∴S△ABC = BC·AD= ×16×4 =32 .
典题精讲
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
A.13 B.19
C.25 D.169
C
典题精讲
已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形.若这两个三角形都是等腰三角形,则( )
A.m2+2mn+n2=0
B.m2-2mn+n2=0
C.m2+2mn-n2=0
D.m2-2mn-n2=0
C
探索新知
例3 如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12 cm,高是20 cm,那么所需彩带最短的是( )
A. 13 cm
B. 4 cm
C. 4 cm
D. 52 cm
D
3
知识点
勾股定理求最小值应用
探索新知
分析:要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理 .
解:有图可知,彩带从易拉罐底端的 A处绕易拉罐 4圈后到达顶端的B处,将易拉罐表面切开展开呈长方形,则螺旋
线长为四个长方形并排后的长方形的对角线长,
∴易拉罐底面周长是12 cm,高是20 cm,∴x2=
(12×4)2+202, 所以彩带最短是52 cm.
探索新知
本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开呈矩形,“化曲面为平面”,用勾股定理解决 .
总 结
典题精讲
如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为______.
典题精讲
如图所示,一圆柱高8 cm,底面半径为2 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A. 20 cm
B. 10 cm
C. 14 cm
D. 无法确定
B
学以致用
小试牛刀
1.勾股定理的验证方法很多,主要是用______法说明,要注意两点:(1)通过割补、拼摆,用相同的直角三角形得到一个图形;
面积
(2)根据拼成的图形得到一个______关系式,通过恒等变形即可得到勾股定理.
例:图①反映的面积关系式为
________________________;
图②反映的面积关系式为_______________________.
面积
小试牛刀
2.在Rt△ABC中,a,b是两直角边,c为斜边,如果已知a,b,那么c2=________;如果已知a,c,那么b2=________;如果已知b,c,那么a2=_______.当不能直接运用勾股定理求线段长度时,则设所求线段的长度为x,并选择一个合适的直角三角形,根据勾股定理,列出含____的方程.
a2+b2
c2-a2
c2-b2
x
小试牛刀
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
3.历史上对勾股定理的一种验证方法采用了如图所示的图形,其中两个全等直角三角形的边AE,EB在一条直线上,其中用到的面积相等的关系式是( )
D
小试牛刀
4.《九章算术》中的“折竹抵地”问题(如图):今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2-6=(10-x)2
B.x2-62=(10-x)2
C.x2+6=(10-x)2
D.x2+62=(10-x)2
D
小试牛刀
5.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为( )
A.0.7 m B.1.5 m
C.2.2 m D.2.4 m
C
小试牛刀
6.如图,AD是△ABC的中线,试说明AB2+AC2=2(AD2+CD2).
解:过点A作AE⊥BC于点E .
在Rt△ABE,Rt△ACE和Rt△ADE中,由勾股定理得
AB2=AE2+BE2,AC2=AE2+EC2,AE2=AD2-DE2,
因为AD是△ABC的中线,所以BD=CD . 所以AB2+AC2=2AD2+2CD2,即AB2+AC2=2(AD2+CD2).
所以AB2+AC2=2AE2+BE2+EC2=2(AD2-DE2)+(BD-DE)2+(CD+DE)2=2AD2-2DE2+BD2-2BD DE+DE2+CD2+2CD DE+DE2
=2AD2+BD2+CD2-2BD DE+2CD DE .
小试牛刀
7.如图,在一棵树的10 m高的B处有两只猴子,其中
一只猴子爬下树,走到离树20 m处的池塘A处,另一只
猴子爬到树顶D后直接跃向池塘A处(假设它跃过的路线为
直线).如果两只猴子所经过的路程相等,求这棵树的高.
【思路点拨】通过设未知数,根据两只猴子经过的路程相等表示出AD
的长度,再利用勾股定理列方程求解.
解:
设BD=x m,由题意知BC+AC=BD+AD,
所以AD=(30-x)m . 所以(10+x)2+202=(30-x)2 . 解得x=5 .
所以x+10=15,即这棵树的高为15 m .
课堂小结
课堂小结
用拼图验证勾股定理的方法:
首先通过拼图找出面积的相等关系,再由面积之间的相等关系并结合图形进行代数变形即可推导出勾股定理 .
它一般都经过以下几个步骤:
拼出图形→写出图形面积的表达式→找出相等关系→恒等变形→导出勾股定理 .
课堂小结
应用勾股定理解题的方法:
(1)添线应用,即题中无直角三角形,可以通过作垂线,构造直角三角形,应用勾股定理求解;
(2)借助方程应用,即题中虽有直角三角形,但已知线段的长不完全是直角三角形的边长,可通过设未知数,构建方程,解答计算问题;
(3)建模应用,即将实际问题建立直角三角形模型,通过勾股定理解决实际问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.3 勾股定理
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
新课精讲
探索新知
1
知识点
勾股定理的实际应用
1.勾股定理的数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,则a2+b2=c2 .
要点精析:
(1)勾股定理适用于任何一个直角三角形;
(2)勾股定理的内容描述的是直角三角形三边之间的数量关系,已知其中任意两边可以求出第三边;
(3)勾股定理的变形公式:a2=c2-b2,b2=c2-a2;
(4)运用勾股定理时,要分清斜边、直角边.
探索新知
2. 基本思想方法:
勾股定理把“形”与“数”有机地结合起来,即把直角三角形这个“形”与三边关系这一“数”结合起来,它是数形结合思想的典范.
易错警示:运用勾股定理时,一定要分清哪条边是斜边 . 在不清楚哪条边是斜边时,要分类讨论,写出所有可能,以免漏解或错解.
探索新知
如图,为了测得湖边上点A和点C间的距离,一观测者在点B设立了一根标杆,使∠ACB=90°.测得 AB=200 m,BC=160 m . 根据测量结果,求点A和点C间的距离 .
例1
解:在△ABC中,
∵∠ACB=90°,
∴AC2+BC2=AB2(勾股定理).
∵AB=200 m,BC=160 m,
答:点A和点C间的距离是120 m .
探索新知
总 结
解决这类实际问题的关键是根据题意,画出图形,建立数学模型,用数学知识解答,把复杂问题简单化、明朗化 .
典题精讲
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在的位置B处与灯塔P之间的距离为( )
A.60 海里
B.45 海里
C.20 海里
D.30 海里
D
典题精讲
2 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8米 B.10米
C.12米 D.14米
B
如图所示,一场暴雨过后,垂直于地面的
一棵树在距地面1.5 m处折断,树尖B恰好
碰到地面,经测量AB=2 m,则树高为____m.
4
探索新知
2
知识点
勾股定理的几何应用
例2 如图,在长为50 mm,宽为40 mm的长方形零件上有两
个圆孔,与孔中心A,B相关的数据如图所示 . 求孔中心A
和B间的距离 .
解:∵△ABC是直角三角形,
∴ AB2=AC2+BC2 .
∵AC=50-15-26=9(mm),
BC=40-18-10=12(mm),
答:孔中心A和B间的距离是15 mm .
探索新知
利用勾股定理求未知边长时,关键要找准斜边,找斜边,就是找直角,直角所对的边就是斜边.
总 结
典题精讲
如图,在△ABC中,AB=AC=12,BC=16 . 求△ABC的面积 .
解:过点A作AD⊥BC,交BC于点D .
∵AB=AC,∴AD是△ABC底边BC上的中线,
∴BD=CD= BC= ×16=8 .
在Rt△ABD中,由勾股定理,得AD2=AB2-BD2=122-82,AD=4 .
∴S△ABC = BC·AD= ×16×4 =32 .
典题精讲
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
A.13 B.19
C.25 D.169
C
典题精讲
已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形.若这两个三角形都是等腰三角形,则( )
A.m2+2mn+n2=0
B.m2-2mn+n2=0
C.m2+2mn-n2=0
D.m2-2mn-n2=0
C
探索新知
例3 如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12 cm,高是20 cm,那么所需彩带最短的是( )
A. 13 cm
B. 4 cm
C. 4 cm
D. 52 cm
D
3
知识点
勾股定理求最小值应用
探索新知
分析:要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理 .
解:有图可知,彩带从易拉罐底端的 A处绕易拉罐 4圈后到达顶端的B处,将易拉罐表面切开展开呈长方形,则螺旋
线长为四个长方形并排后的长方形的对角线长,
∴易拉罐底面周长是12 cm,高是20 cm,∴x2=
(12×4)2+202, 所以彩带最短是52 cm.
探索新知
本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开呈矩形,“化曲面为平面”,用勾股定理解决 .
总 结
典题精讲
如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为______.
典题精讲
如图所示,一圆柱高8 cm,底面半径为2 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A. 20 cm
B. 10 cm
C. 14 cm
D. 无法确定
B
学以致用
小试牛刀
1.勾股定理的验证方法很多,主要是用______法说明,要注意两点:(1)通过割补、拼摆,用相同的直角三角形得到一个图形;
面积
(2)根据拼成的图形得到一个______关系式,通过恒等变形即可得到勾股定理.
例:图①反映的面积关系式为
________________________;
图②反映的面积关系式为_______________________.
面积
小试牛刀
2.在Rt△ABC中,a,b是两直角边,c为斜边,如果已知a,b,那么c2=________;如果已知a,c,那么b2=________;如果已知b,c,那么a2=_______.当不能直接运用勾股定理求线段长度时,则设所求线段的长度为x,并选择一个合适的直角三角形,根据勾股定理,列出含____的方程.
a2+b2
c2-a2
c2-b2
x
小试牛刀
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
3.历史上对勾股定理的一种验证方法采用了如图所示的图形,其中两个全等直角三角形的边AE,EB在一条直线上,其中用到的面积相等的关系式是( )
D
小试牛刀
4.《九章算术》中的“折竹抵地”问题(如图):今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2-6=(10-x)2
B.x2-62=(10-x)2
C.x2+6=(10-x)2
D.x2+62=(10-x)2
D
小试牛刀
5.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为( )
A.0.7 m B.1.5 m
C.2.2 m D.2.4 m
C
小试牛刀
6.如图,AD是△ABC的中线,试说明AB2+AC2=2(AD2+CD2).
解:过点A作AE⊥BC于点E .
在Rt△ABE,Rt△ACE和Rt△ADE中,由勾股定理得
AB2=AE2+BE2,AC2=AE2+EC2,AE2=AD2-DE2,
因为AD是△ABC的中线,所以BD=CD . 所以AB2+AC2=2AD2+2CD2,即AB2+AC2=2(AD2+CD2).
所以AB2+AC2=2AE2+BE2+EC2=2(AD2-DE2)+(BD-DE)2+(CD+DE)2=2AD2-2DE2+BD2-2BD DE+DE2+CD2+2CD DE+DE2
=2AD2+BD2+CD2-2BD DE+2CD DE .
小试牛刀
7.如图,在一棵树的10 m高的B处有两只猴子,其中
一只猴子爬下树,走到离树20 m处的池塘A处,另一只
猴子爬到树顶D后直接跃向池塘A处(假设它跃过的路线为
直线).如果两只猴子所经过的路程相等,求这棵树的高.
【思路点拨】通过设未知数,根据两只猴子经过的路程相等表示出AD
的长度,再利用勾股定理列方程求解.
解:
设BD=x m,由题意知BC+AC=BD+AD,
所以AD=(30-x)m . 所以(10+x)2+202=(30-x)2 . 解得x=5 .
所以x+10=15,即这棵树的高为15 m .
课堂小结
课堂小结
用拼图验证勾股定理的方法:
首先通过拼图找出面积的相等关系,再由面积之间的相等关系并结合图形进行代数变形即可推导出勾股定理 .
它一般都经过以下几个步骤:
拼出图形→写出图形面积的表达式→找出相等关系→恒等变形→导出勾股定理 .
课堂小结
应用勾股定理解题的方法:
(1)添线应用,即题中无直角三角形,可以通过作垂线,构造直角三角形,应用勾股定理求解;
(2)借助方程应用,即题中虽有直角三角形,但已知线段的长不完全是直角三角形的边长,可通过设未知数,构建方程,解答计算问题;
(3)建模应用,即将实际问题建立直角三角形模型,通过勾股定理解决实际问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
