冀教版(新)八上-17.3 勾股定理 第三课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-17.3 勾股定理 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:17 | ||
图片预览








文档简介
(共28张PPT)
17.3 勾股定理
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
通过前边的学习我们知道直角三角形的三边有特殊的数量关系,那么我们如何识别一个三角形是不是直角三角形呢?今天,我们学习一种新的方法!
新课精讲
探索新知
1
知识点
由边的数量关系判定直角三角形
如果△ABC的三边a,b, c满足a2+b2=c2,那么∠C是直角吗?
在△ABC中,由边的关系a2+b2=c2,推导出∠C是直角较难做到 . 若作一个与△ABC全等的直角三角形,则可借助于全等的性质来说明∠C是直角 .
已知:如图,在△ABC 中,AB = c,BC = a,
CA = b,且 a2 + b2 = c2 .
求证:∠C=90° .
探索新知
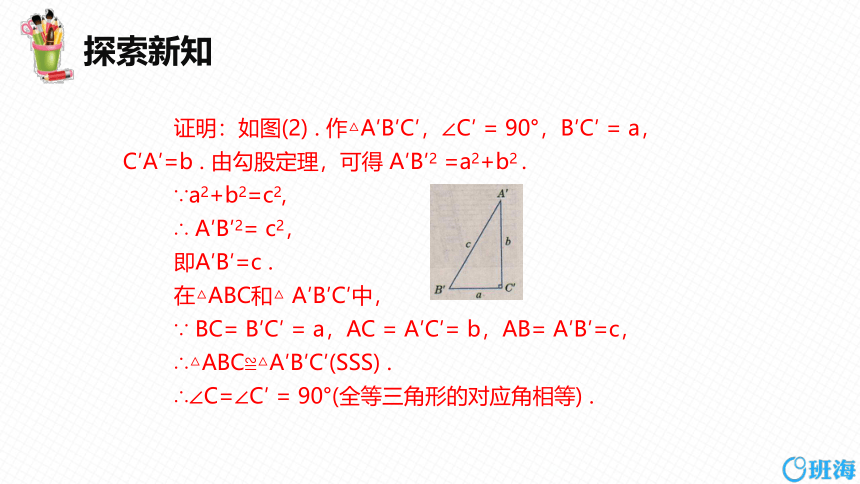
证明:如图(2) . 作△A′B′C′,∠C′ = 90°,B′C′ = a,
C′A′=b . 由勾股定理,可得 A′B′2 =a2+b2 .
∵a2+b2=c2,
∴ A′B′2= c2,
即A′B′=c .
在△ABC和△ A′B′C′中,
∵ BC= B′C′ = a,AC = A′C′= b,AB= A′B′=c,
∴△ABC≌△A′B′C′(SSS) .
∴∠C=∠C′ = 90°(全等三角形的对应角相等) .
探索新知
归 纳
如果三角形的三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形 .
探索新知
图是一个机器零件示意图,∠ACD=90°是这种零件合格的一项指标.现测得 AB=4 cm,BC= 3 cm,CD =12 cm,AD = 13 cm,∠ABC=90° . 根据这些条件,能否知道∠ACD =90°?
例1
解:
在△ABC中,∵∠ABC = 90°,
∴ AC2 =AB2 +BC2 (勾股定理) .
∵AB=4,BC=3,
∴ AC2 = 32+42 = 52 . ∴ AC=5 .
在△ACD中,∵ AC=5,CD = 12,AD= 13,
∴ AC2+CD2 = 52 +122=169,AD2 =132 =169 .
∴ AC2+CD2=AD2 . ∴∠ACD=90°(勾股定理的逆定理) .
所以,根据这些条件,能知道∠ACD= 90° .
探索新知
总 结
利用勾股定理的逆定理构建直角三角形解决问题的方法:先通过勾股定理的逆定理证明一个三角形是直角三角形,然后利用直角得到另一个直角三角形,在另一个直角三角形中运用勾股定理求边长,这是勾股定理及其逆定理常用的综合解题思路,这种方法常用在具有公共直角或者两直角互为邻补角的两个直角三角形中.
典题精讲
下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
2 已知△ABC的三边长分别为5,12,13,则△ABC的面积为( )
A.30 B.60
C.78 D.无法确定
D
A
典题精讲
解:∵AD是△ABC的中线,
∴BD= BC=8 .
在△ABD中,∵AB=17,BD=8,AD=15,
∴AB2=172=289,BD2+AD2=82+152=64+225=289,
∴BD2+AD2=AB2,
∴△ABD为直角三角形,且∠ADB=90°,
∴△ADC是直角三角形.在Rt△ADC中,AC=
=17,∴AB=AC .
如图,在△ABC中,AB=17,BC=16,BC边上的中线AD等于
15,试说明AB=AC .
探索新知
2
知识点
勾股数
1.勾股数:能够成为直角三角形三条边长的三个正整数.常见的勾股数有:3,4,5;5,12,13;8,15,17;7,24,25;9,40,41;….
要点精析:
(1)勾股数有无数组;
(2)一组勾股数中各数的相同倍数构成一组新的勾股数,如3,4,5是勾股数,则6,8,10和9,12,15也是勾股数;即如果a,b,c是一组勾股数,那么na,nb,nc(n为正整数)也是一组勾股数.
探索新知
2.判断勾股数的方法:
(1)确定是否是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的平方.
易错警示:
勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方.
探索新知
例2 下面四组数中是勾股数的一组是( )
A.6,7,8 B.5,8,13
C.1.5,2,2.5 D.21,28,35
导引:根据勾股数的定义:满足a2+b2=c2的三个正整数a,b,c称为勾股数.A.62+72≠82,不能构成勾股数,故错误;B.52+82≠132,不能构成勾股数,故错误;C.1.5和2.5不是整数,所以不能构成勾股数,故错误;D.212+282=352,能构成勾股数,故正确.故选D .
D
探索新知
确定勾股数的方法:首先看这三个数是否是正整数;然后看较小两个数的平方和是否等于最大数的平方.记住一些常见的勾股数可以提高解题速度.常见的勾股数有3,4,5;5,12,13;8,15,17;7,24,25;9,40,41;….
总 结
典题精讲
若直角三角形的三边长为三个连续的偶数,则它的三边长分别
是( )
A.3,4,5
B.6,8,10
C.3,4,6
D.4,6,8
B
典题精讲
2 下列各组数中,不是勾股数的是( )
A.5,12,13 B.7,24,25
C.8,12,15 D.3k,4k,5k(k为正整数)
3 下面几组数中,为勾股数的一组是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1
C
B
学以致用
小试牛刀
1.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是____________.
直角三角形
2.满足a2+b2=c2的三个正整数,称为_________.
3.下列各组数能构成勾股数的是______ (填序号).
① 6,8,10;② 7,8,10;③ , ,1 .
勾股数
①
小试牛刀
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.△ABC不是直角三角形
A
5.下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5
C.3,4,6 D.3,4,7
C
小试牛刀
6.下列各组数中,是勾股数的是( )
A.14,36,39 B.8,24,25
C.8,15,17 D.10,20,26
C
7.下列几组数:
①9,12,15;②8,15,17;③7,24,25;
④n2-1,2n,n2+1(n是大于1的整数).
其中是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
D
小试牛刀
8. 如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且
∠B=90° . 求∠BAD的度数.
解:连接AC . 因为∠B=90°,AB=BC=2,
所以△ABC为等腰直角三角形. 所以∠BAC=45° .
又因为CD=3,AD=1,
所以AC2+AD2=AB2+BC2+AD2=4+4+1=9,CD2=9 .
所以AC2+AD2=CD2 .
所以△ACD是直角三角形且∠CAD=90° .
所以∠BAD=45°+90°=135° .
小试牛刀
9.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,
且PA=3,PB=1,PC=2 . 求∠BPC的度数.
【思路点拨】解答本题要紧扣两个切入点:
(1)由于∠BPC是一钝角,想办法将其分割成一直角与一特殊角
(30°,60°,45°)的和的形式;
(2)用旋转法将△CPB绕点C顺时针旋转90°到△CP′A的位置.
小试牛刀
解:如图,将△CPB绕点C顺时针旋转90°得△CP′A,则P′C=PC=2,P′A=PB=1,∠BPC=∠AP′C,连接PP′ .
∵∠PCP′=90°,∴PP′2=22+22=8 .
∵P′A=1,PA=3,
∴PP′2+P′A2=8+1=9,PA2=9 .
∴PP′2+P′A2=PA2 . ∴∠AP′P=90° .
易知∠CP′P=45°,
∴∠BPC=∠AP′C=∠AP′P+∠CP′P=90°+45°=135° .
课堂小结
课堂小结
勾股定理及其逆定理的应用:
(1)单一应用:先由勾股定理的逆定理得出直角三角形后,再求这个直角三角形的角度和面积;
(2)综合应用:先由勾股定理求出三角形的边长,再由勾股定理的逆定理确定三角形的形状,进而解决其他问题;
(3)逆向应用:如果一个三角形两条较小边长的平方和不等于最大边长的平方,那么这个三角形就不是直角三角形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.3 勾股定理
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
通过前边的学习我们知道直角三角形的三边有特殊的数量关系,那么我们如何识别一个三角形是不是直角三角形呢?今天,我们学习一种新的方法!
新课精讲
探索新知
1
知识点
由边的数量关系判定直角三角形
如果△ABC的三边a,b, c满足a2+b2=c2,那么∠C是直角吗?
在△ABC中,由边的关系a2+b2=c2,推导出∠C是直角较难做到 . 若作一个与△ABC全等的直角三角形,则可借助于全等的性质来说明∠C是直角 .
已知:如图,在△ABC 中,AB = c,BC = a,
CA = b,且 a2 + b2 = c2 .
求证:∠C=90° .
探索新知
证明:如图(2) . 作△A′B′C′,∠C′ = 90°,B′C′ = a,
C′A′=b . 由勾股定理,可得 A′B′2 =a2+b2 .
∵a2+b2=c2,
∴ A′B′2= c2,
即A′B′=c .
在△ABC和△ A′B′C′中,
∵ BC= B′C′ = a,AC = A′C′= b,AB= A′B′=c,
∴△ABC≌△A′B′C′(SSS) .
∴∠C=∠C′ = 90°(全等三角形的对应角相等) .
探索新知
归 纳
如果三角形的三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形 .
探索新知
图是一个机器零件示意图,∠ACD=90°是这种零件合格的一项指标.现测得 AB=4 cm,BC= 3 cm,CD =12 cm,AD = 13 cm,∠ABC=90° . 根据这些条件,能否知道∠ACD =90°?
例1
解:
在△ABC中,∵∠ABC = 90°,
∴ AC2 =AB2 +BC2 (勾股定理) .
∵AB=4,BC=3,
∴ AC2 = 32+42 = 52 . ∴ AC=5 .
在△ACD中,∵ AC=5,CD = 12,AD= 13,
∴ AC2+CD2 = 52 +122=169,AD2 =132 =169 .
∴ AC2+CD2=AD2 . ∴∠ACD=90°(勾股定理的逆定理) .
所以,根据这些条件,能知道∠ACD= 90° .
探索新知
总 结
利用勾股定理的逆定理构建直角三角形解决问题的方法:先通过勾股定理的逆定理证明一个三角形是直角三角形,然后利用直角得到另一个直角三角形,在另一个直角三角形中运用勾股定理求边长,这是勾股定理及其逆定理常用的综合解题思路,这种方法常用在具有公共直角或者两直角互为邻补角的两个直角三角形中.
典题精讲
下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
2 已知△ABC的三边长分别为5,12,13,则△ABC的面积为( )
A.30 B.60
C.78 D.无法确定
D
A
典题精讲
解:∵AD是△ABC的中线,
∴BD= BC=8 .
在△ABD中,∵AB=17,BD=8,AD=15,
∴AB2=172=289,BD2+AD2=82+152=64+225=289,
∴BD2+AD2=AB2,
∴△ABD为直角三角形,且∠ADB=90°,
∴△ADC是直角三角形.在Rt△ADC中,AC=
=17,∴AB=AC .
如图,在△ABC中,AB=17,BC=16,BC边上的中线AD等于
15,试说明AB=AC .
探索新知
2
知识点
勾股数
1.勾股数:能够成为直角三角形三条边长的三个正整数.常见的勾股数有:3,4,5;5,12,13;8,15,17;7,24,25;9,40,41;….
要点精析:
(1)勾股数有无数组;
(2)一组勾股数中各数的相同倍数构成一组新的勾股数,如3,4,5是勾股数,则6,8,10和9,12,15也是勾股数;即如果a,b,c是一组勾股数,那么na,nb,nc(n为正整数)也是一组勾股数.
探索新知
2.判断勾股数的方法:
(1)确定是否是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的平方.
易错警示:
勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方.
探索新知
例2 下面四组数中是勾股数的一组是( )
A.6,7,8 B.5,8,13
C.1.5,2,2.5 D.21,28,35
导引:根据勾股数的定义:满足a2+b2=c2的三个正整数a,b,c称为勾股数.A.62+72≠82,不能构成勾股数,故错误;B.52+82≠132,不能构成勾股数,故错误;C.1.5和2.5不是整数,所以不能构成勾股数,故错误;D.212+282=352,能构成勾股数,故正确.故选D .
D
探索新知
确定勾股数的方法:首先看这三个数是否是正整数;然后看较小两个数的平方和是否等于最大数的平方.记住一些常见的勾股数可以提高解题速度.常见的勾股数有3,4,5;5,12,13;8,15,17;7,24,25;9,40,41;….
总 结
典题精讲
若直角三角形的三边长为三个连续的偶数,则它的三边长分别
是( )
A.3,4,5
B.6,8,10
C.3,4,6
D.4,6,8
B
典题精讲
2 下列各组数中,不是勾股数的是( )
A.5,12,13 B.7,24,25
C.8,12,15 D.3k,4k,5k(k为正整数)
3 下面几组数中,为勾股数的一组是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1
C
B
学以致用
小试牛刀
1.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是____________.
直角三角形
2.满足a2+b2=c2的三个正整数,称为_________.
3.下列各组数能构成勾股数的是______ (填序号).
① 6,8,10;② 7,8,10;③ , ,1 .
勾股数
①
小试牛刀
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.△ABC不是直角三角形
A
5.下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5
C.3,4,6 D.3,4,7
C
小试牛刀
6.下列各组数中,是勾股数的是( )
A.14,36,39 B.8,24,25
C.8,15,17 D.10,20,26
C
7.下列几组数:
①9,12,15;②8,15,17;③7,24,25;
④n2-1,2n,n2+1(n是大于1的整数).
其中是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
D
小试牛刀
8. 如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且
∠B=90° . 求∠BAD的度数.
解:连接AC . 因为∠B=90°,AB=BC=2,
所以△ABC为等腰直角三角形. 所以∠BAC=45° .
又因为CD=3,AD=1,
所以AC2+AD2=AB2+BC2+AD2=4+4+1=9,CD2=9 .
所以AC2+AD2=CD2 .
所以△ACD是直角三角形且∠CAD=90° .
所以∠BAD=45°+90°=135° .
小试牛刀
9.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,
且PA=3,PB=1,PC=2 . 求∠BPC的度数.
【思路点拨】解答本题要紧扣两个切入点:
(1)由于∠BPC是一钝角,想办法将其分割成一直角与一特殊角
(30°,60°,45°)的和的形式;
(2)用旋转法将△CPB绕点C顺时针旋转90°到△CP′A的位置.
小试牛刀
解:如图,将△CPB绕点C顺时针旋转90°得△CP′A,则P′C=PC=2,P′A=PB=1,∠BPC=∠AP′C,连接PP′ .
∵∠PCP′=90°,∴PP′2=22+22=8 .
∵P′A=1,PA=3,
∴PP′2+P′A2=8+1=9,PA2=9 .
∴PP′2+P′A2=PA2 . ∴∠AP′P=90° .
易知∠CP′P=45°,
∴∠BPC=∠AP′C=∠AP′P+∠CP′P=90°+45°=135° .
课堂小结
课堂小结
勾股定理及其逆定理的应用:
(1)单一应用:先由勾股定理的逆定理得出直角三角形后,再求这个直角三角形的角度和面积;
(2)综合应用:先由勾股定理求出三角形的边长,再由勾股定理的逆定理确定三角形的形状,进而解决其他问题;
(3)逆向应用:如果一个三角形两条较小边长的平方和不等于最大边长的平方,那么这个三角形就不是直角三角形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
