冀教版(新)八上-17.3 勾股定理 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)八上-17.3 勾股定理 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:17 | ||
图片预览










文档简介
(共32张PPT)
17.3 勾股定理
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图是2002年在北京召开的国际数学家大会(ICM-2002)的会标 . 它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图 . 用弦图证明勾股定理在数学史上有着重要的地位 .
新课精讲
探索新知
1
知识点
勾股定理
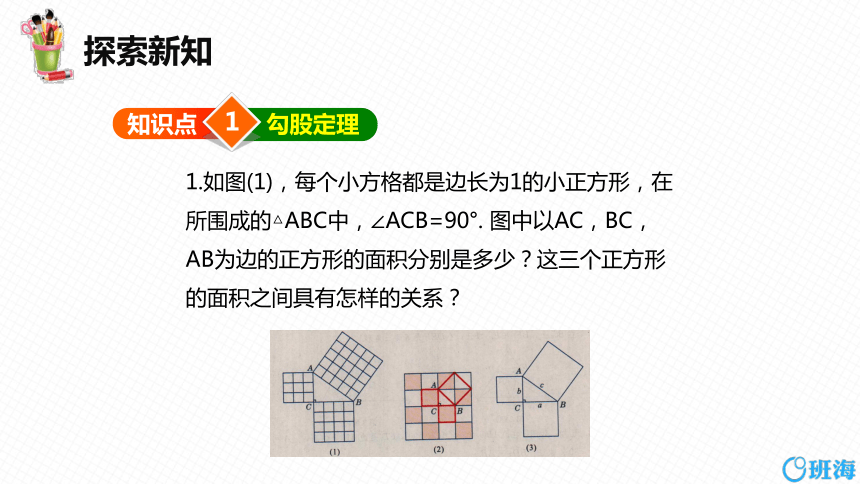
1.如图(1),每个小方格都是边长为1的小正方形,在所围成的△ABC中,∠ACB=90°. 图中以AC,BC,AB为边的正方形的面积分别是多少?这三个正方形的面积之间具有怎样的关系?
探索新知
2. 图(2)是用大小相同的两种颜色的正方形地砖铺成的地面示意图,∠ACB=90°. 分别以AC,BC,AB为边的三个正方形(红色框标出)的面积之间有怎样的关系?
3. 如图(3),在△ABC中,∠ACB=90°,请你猜想:分别以AC,BC,AB为边的三个正方形的面积之间也具有图(1)和图(2)中三个正方形的面积之间所具有的关系吗?
如果具有这种关系,请用图(3)中Rt△ABC的边把这种关系表示出来 .
探索新知
归 纳
通过探究可知:在直角三角形中,两条直角边的平方和等于斜边的平方 .
探索新知
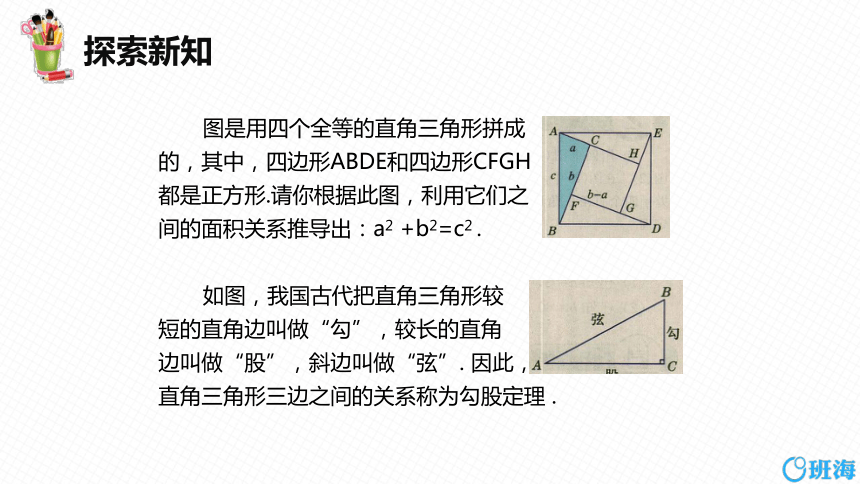
图是用四个全等的直角三角形拼成
的,其中,四边形ABDE和四边形CFGH
都是正方形.请你根据此图,利用它们之
间的面积关系推导出:a2 +b2=c2 .
如图,我国古代把直角三角形较
短的直角边叫做“勾”,较长的直角
边叫做“股”,斜边叫做“弦”. 因此,
直角三角形三边之间的关系称为勾股定理 .
探索新知
归 纳
如果直角三角形两直角边分别为a,b斜边为c,那么a2+b2=c2 .
勾股定理也可叙述为:直角三角形两直角边的平方和等于斜边的平方 .
探索新知
分析:本题考查了等腰三角形三线合一的性质,即等腰三角形底边上的中线,底边上的高重合,利用三线合一的性质求得线段的长度后,再利用勾股定理求出AD边的长度 .
解:根据等腰三角形的三线合一,AD是底边上的高,可得
AD⊥BD . 即BD= BC= ×6=3(cm) . 在Rt△ABD中,
由勾股定理,得AB2=BD2+AD2,所以AD=4 cm .
如图所示,等腰三角形ABC中,AB=AC ,AD是底边上的高,若AB=5 cm,BC=6 cm,则AD= cm.
例1
A
C
D
B
4
探索新知
总 结
在直角三角形中应用勾股定理求边长时,要分清斜边和直角边,避免盲目代入勾股定理的公式 .
典题精讲
1 下列说法中正确的是( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△ABC中,∠C=90°,则a2+b2=c2
D.在Rt△ABC中,∠B=90°,则a2+b2=c2
2 若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则
下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
C
典题精讲
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
A
探索新知
2
知识点
勾股定理与图形的面积
例2 如图所示,在△ABC中,∠ACB=90°,以△ABC的各
边为边在△ABC外作三个正方形,S1,S2 ,S3分别表示这
三个正方形的面积,S1=81,S3=225,则S2=______.
分析:要求S2的面积,需要知道正方形的边长或边长的平方,利用勾股定理可以解答 .
解:由勾股定理,得AC2+BC2=AB2 . 又∵S1=AC2,S2=BC2,S3=AB2 ,∴S1+S2=S3 . 即S2=S3-S1=225—81=144 . 故填144 .
点拨:本题将勾股定理与正方形面积公式结合起来,通过勾股定理解决正方形面积的问题,充分体现了它们之间存在的联系.
144
探索新知
正方形和直角三角形相结合可以求出图形的面积 .
总 结
如图所示,分别以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8.试求S3 .
解析:把正方形的面积用边长的平方表示,然后利用勾股定理求解.
典题精讲
解:在Rt△ABC中,由勾股定理得BC2+AC2=AB2.
所以S3=AB2=BC2+AC2=S1+S2=12.
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
A.3 B.4 C.5 D.7
D
典题精讲
典题精讲
如图,已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
A.S1>S2 B.S1<S2
C.S1=S2 D.不能确定
C
学以致用
小试牛刀
1.直角三角形____________________等于_____________.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么________________.
两直角边的平方和
斜边的平方
a2+b2=c2
2.勾股定理通常是用________法来验证的,因此很多涉及直角三角形的图形面积问题,通常用___________来解决.
面积
勾股定理
3.在Rt△ABC中,斜边长BC=3,则AB2+AC2+BC2的值为( )
A.18 B.9 C.6 D.无法计算
A
小试牛刀
4.我国三国时期数学家赵爽为了验证勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图①所示.在图②中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为________.
10
小试牛刀
5.如图,在△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
C
小试牛刀
6.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
C
小试牛刀
7.如图,在Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.4π
C.8π D.16π
A
小试牛刀
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=20 m,BC=15 m,CD=7 m,求四边形ABCD的面积.
解:如图,连接AC .∵∠B=∠D=90°,
∴△ABC与△ACD都是直角三角形.
在Rt△ABC中,根据勾股定理,
得AC2=AB2+BC2=202+152=625,则AC=25 .
在Rt△ACD中,根据勾股定理,
得AD2=AC2-CD2=252-72=576,则AD=24 .
故S四边形ABCD=S△ABC+S△ACD= AB BC+ AD CD
= ×20×15+ ×24×7=234(m2)
小试牛刀
9.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上高的长.
【思路点拨】倍长中线BD,说明2BD
等于△ABC中BC边上的高.
解:
(1)∵DB⊥BC,BC=4,CD=5,
∴在Rt△BCD中,根据勾股定理得DB=3.
小试牛刀
(2)如图,延长BD至E,使DE=DB,连接AE.
∵D是AC边的中点,
∴AD=CD.
9.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(2)在△ABC中,求BC边上高的长.
在△EDA和△BDC中,AD=CD,∠ADE=∠CDB,DE=DB,
∴△EDA≌△BDC(SAS).
∴∠DAE=∠DCB . AE∥BC .
∵DB⊥BC,∴△ABC中BC边上的高的长等于BE的长.
易知BE=2BD=6,∴BC边上的高的长为6.
课堂小结
课堂小结
运用勾股定理时应注意以下几点:
(1)遇到求线段长度的问题时,能想到利用勾股定理 .
(2)必须把要求的线段归结到直角三角形中去(没有直角三角形,可以通过作辅助线构造直角三角形),切记乱用勾股定理 .
(3)分清组成直角三角形的线段中哪条是直角边,哪条是斜边 .
课堂小结
勾股定理适用的前提条件是直角三角形:
由公式a2+b2=c2可知,在直角三角形中,已知任意两条边长,可求第三条边长 .
在应用公式计算时要会灵活变形,常常要与乘法公式结合适用;如c2=a2+b2=(a+b)2-2ab或c2=a2+b2=(a-b)2+2ab;a2=c2-b2=(c+b)(c-b)等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.3 勾股定理
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图是2002年在北京召开的国际数学家大会(ICM-2002)的会标 . 它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图 . 用弦图证明勾股定理在数学史上有着重要的地位 .
新课精讲
探索新知
1
知识点
勾股定理
1.如图(1),每个小方格都是边长为1的小正方形,在所围成的△ABC中,∠ACB=90°. 图中以AC,BC,AB为边的正方形的面积分别是多少?这三个正方形的面积之间具有怎样的关系?
探索新知
2. 图(2)是用大小相同的两种颜色的正方形地砖铺成的地面示意图,∠ACB=90°. 分别以AC,BC,AB为边的三个正方形(红色框标出)的面积之间有怎样的关系?
3. 如图(3),在△ABC中,∠ACB=90°,请你猜想:分别以AC,BC,AB为边的三个正方形的面积之间也具有图(1)和图(2)中三个正方形的面积之间所具有的关系吗?
如果具有这种关系,请用图(3)中Rt△ABC的边把这种关系表示出来 .
探索新知
归 纳
通过探究可知:在直角三角形中,两条直角边的平方和等于斜边的平方 .
探索新知
图是用四个全等的直角三角形拼成
的,其中,四边形ABDE和四边形CFGH
都是正方形.请你根据此图,利用它们之
间的面积关系推导出:a2 +b2=c2 .
如图,我国古代把直角三角形较
短的直角边叫做“勾”,较长的直角
边叫做“股”,斜边叫做“弦”. 因此,
直角三角形三边之间的关系称为勾股定理 .
探索新知
归 纳
如果直角三角形两直角边分别为a,b斜边为c,那么a2+b2=c2 .
勾股定理也可叙述为:直角三角形两直角边的平方和等于斜边的平方 .
探索新知
分析:本题考查了等腰三角形三线合一的性质,即等腰三角形底边上的中线,底边上的高重合,利用三线合一的性质求得线段的长度后,再利用勾股定理求出AD边的长度 .
解:根据等腰三角形的三线合一,AD是底边上的高,可得
AD⊥BD . 即BD= BC= ×6=3(cm) . 在Rt△ABD中,
由勾股定理,得AB2=BD2+AD2,所以AD=4 cm .
如图所示,等腰三角形ABC中,AB=AC ,AD是底边上的高,若AB=5 cm,BC=6 cm,则AD= cm.
例1
A
C
D
B
4
探索新知
总 结
在直角三角形中应用勾股定理求边长时,要分清斜边和直角边,避免盲目代入勾股定理的公式 .
典题精讲
1 下列说法中正确的是( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△ABC中,∠C=90°,则a2+b2=c2
D.在Rt△ABC中,∠B=90°,则a2+b2=c2
2 若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则
下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
C
典题精讲
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
A
探索新知
2
知识点
勾股定理与图形的面积
例2 如图所示,在△ABC中,∠ACB=90°,以△ABC的各
边为边在△ABC外作三个正方形,S1,S2 ,S3分别表示这
三个正方形的面积,S1=81,S3=225,则S2=______.
分析:要求S2的面积,需要知道正方形的边长或边长的平方,利用勾股定理可以解答 .
解:由勾股定理,得AC2+BC2=AB2 . 又∵S1=AC2,S2=BC2,S3=AB2 ,∴S1+S2=S3 . 即S2=S3-S1=225—81=144 . 故填144 .
点拨:本题将勾股定理与正方形面积公式结合起来,通过勾股定理解决正方形面积的问题,充分体现了它们之间存在的联系.
144
探索新知
正方形和直角三角形相结合可以求出图形的面积 .
总 结
如图所示,分别以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8.试求S3 .
解析:把正方形的面积用边长的平方表示,然后利用勾股定理求解.
典题精讲
解:在Rt△ABC中,由勾股定理得BC2+AC2=AB2.
所以S3=AB2=BC2+AC2=S1+S2=12.
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
A.3 B.4 C.5 D.7
D
典题精讲
典题精讲
如图,已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
A.S1>S2 B.S1<S2
C.S1=S2 D.不能确定
C
学以致用
小试牛刀
1.直角三角形____________________等于_____________.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么________________.
两直角边的平方和
斜边的平方
a2+b2=c2
2.勾股定理通常是用________法来验证的,因此很多涉及直角三角形的图形面积问题,通常用___________来解决.
面积
勾股定理
3.在Rt△ABC中,斜边长BC=3,则AB2+AC2+BC2的值为( )
A.18 B.9 C.6 D.无法计算
A
小试牛刀
4.我国三国时期数学家赵爽为了验证勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图①所示.在图②中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为________.
10
小试牛刀
5.如图,在△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
C
小试牛刀
6.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
C
小试牛刀
7.如图,在Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.4π
C.8π D.16π
A
小试牛刀
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=20 m,BC=15 m,CD=7 m,求四边形ABCD的面积.
解:如图,连接AC .∵∠B=∠D=90°,
∴△ABC与△ACD都是直角三角形.
在Rt△ABC中,根据勾股定理,
得AC2=AB2+BC2=202+152=625,则AC=25 .
在Rt△ACD中,根据勾股定理,
得AD2=AC2-CD2=252-72=576,则AD=24 .
故S四边形ABCD=S△ABC+S△ACD= AB BC+ AD CD
= ×20×15+ ×24×7=234(m2)
小试牛刀
9.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上高的长.
【思路点拨】倍长中线BD,说明2BD
等于△ABC中BC边上的高.
解:
(1)∵DB⊥BC,BC=4,CD=5,
∴在Rt△BCD中,根据勾股定理得DB=3.
小试牛刀
(2)如图,延长BD至E,使DE=DB,连接AE.
∵D是AC边的中点,
∴AD=CD.
9.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(2)在△ABC中,求BC边上高的长.
在△EDA和△BDC中,AD=CD,∠ADE=∠CDB,DE=DB,
∴△EDA≌△BDC(SAS).
∴∠DAE=∠DCB . AE∥BC .
∵DB⊥BC,∴△ABC中BC边上的高的长等于BE的长.
易知BE=2BD=6,∴BC边上的高的长为6.
课堂小结
课堂小结
运用勾股定理时应注意以下几点:
(1)遇到求线段长度的问题时,能想到利用勾股定理 .
(2)必须把要求的线段归结到直角三角形中去(没有直角三角形,可以通过作辅助线构造直角三角形),切记乱用勾股定理 .
(3)分清组成直角三角形的线段中哪条是直角边,哪条是斜边 .
课堂小结
勾股定理适用的前提条件是直角三角形:
由公式a2+b2=c2可知,在直角三角形中,已知任意两条边长,可求第三条边长 .
在应用公式计算时要会灵活变形,常常要与乘法公式结合适用;如c2=a2+b2=(a+b)2-2ab或c2=a2+b2=(a-b)2+2ab;a2=c2-b2=(c+b)(c-b)等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
