冀教版(新)八上-17.4 直角三角形全等的判定【优质课件】
文档属性
| 名称 | 冀教版(新)八上-17.4 直角三角形全等的判定【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:17 | ||
图片预览






文档简介
(共27张PPT)
17.4 直角三角形全等的判定
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
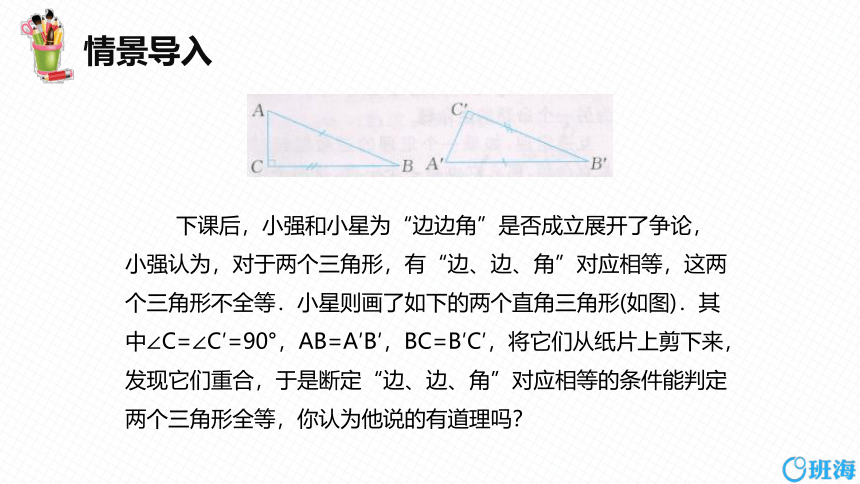
下课后,小强和小星为“边边角”是否成立展开了争论,小强认为,对于两个三角形,有“边、边、角”对应相等,这两个三角形不全等.小星则画了如下的两个直角三角形(如图).其中∠C=∠C′=90°,AB=A′B′,BC=B′C′,将它们从纸片上剪下来,发现它们重合,于是断定“边、边、角”对应相等的条件能判定两个三角形全等,你认为他说的有道理吗?
新课精讲
探索新知
1
知识点
判定两直角三角形全等的方法:斜边、直角边
我们已经知道,三边对应相等的两个三角形全等 .
由勾股定理可知,两边对应相等的两个直角三角形,其第三边一定相等 . 从而,这两个直角三角形一定全等 . 因此,斜边和一条直角边对应相等的两个直角三角形全等 . 证明过程如下:
探索新知
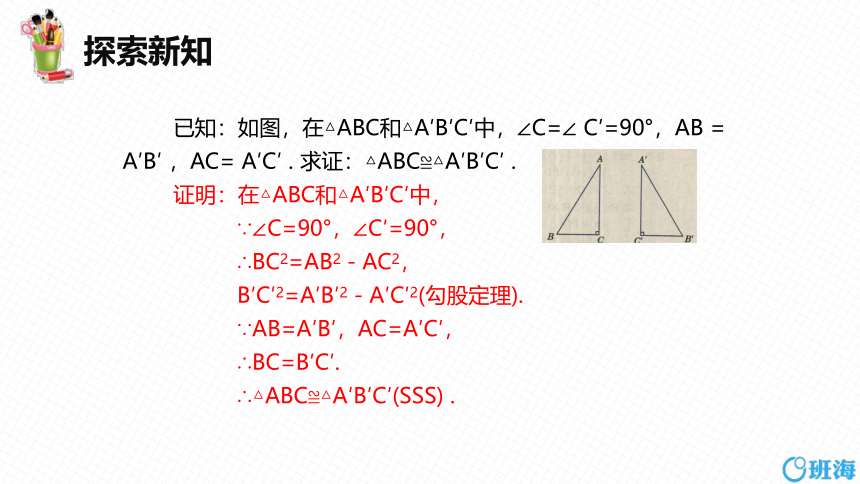
已知:如图,在△ABC和△A′B′C′中,∠C=∠ C′=90°,AB = A′B′ ,AC= A′C′ . 求证:△ABC≌△A′B′C′ .
证明:在△ABC和△A′B′C′中,
∵∠C=90°,∠C′=90°,
∴BC2=AB2-AC2,
B′C′2=A′B′2-A′C′2(勾股定理).
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS) .
探索新知
归 纳
斜边和直角边对应相等的两个直角三角形全等 .
这个定理可以简写为“斜边、直角边”或“HL”.
探索新知
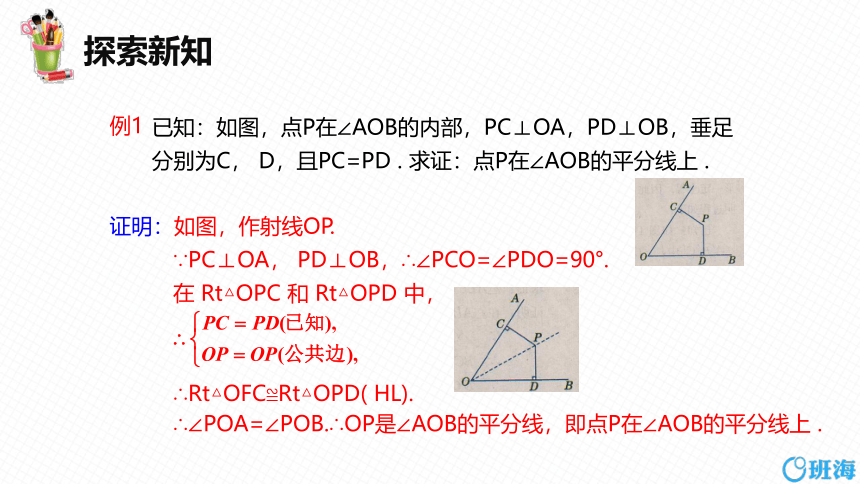
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C, D,且PC=PD . 求证:点P在∠AOB的平分线上 .
例1
证明:如图,作射线OP.
∵PC⊥OA, PD⊥OB,∴∠PCO=∠PDO=90°.
在 Rt△OPC 和 Rt△OPD 中,
∴Rt△OFC≌Rt△OPD( HL).
∴∠POA=∠POB.∴OP是∠AOB的平分线,即点P在∠AOB的平分线上 .
探索新知
总 结
应用“HL”判定两个直角三角形全等,书写时,必须强调是直角三角形.
典题精讲
如图,在△ABC中,AB=CB,∠ABC= 90°,F为AB延长线上一
点,点E在BC上,且AE=CF . 求证: Rt△ABE≌Rt△CBF .
证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90° .
在Rt△ABE和Rt△CBF中,
∵
∴Rt△ABE≌Rt△CBF(HL).
典题精讲
2 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ ABC与Rt△ABD全等.以下给出的条件正确的是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3 下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.两条边对应相等
A
D
证明:在Rt△ABC和Rt△ABD中,
∵AC=AD,AB=AB,
∴Rt△ABC≌Rt△ABD(HL),∴∠CAB=∠DAB .
在△AEC和△AED中,∵AC=AD,∠CAE=∠DAE,AE=AE,
∴△AEC≌△AED(SAS), ∴CE=DE .
探索新知
2
知识点
直角三角形全等的综合判定
例2 [探究题] 如图所示,已知∠ACB=∠ADB=90°,
AC=AD,E是AB上任意一点.求证:CE=DE .
探索新知
直角三角形是一类特殊的三角形,它具有一般三角形的所有性质,因此,判定两个直角三角形全等时,完全可以采用一般三角形全等的判定方法.由于直角三角形中有一个直角,而直角都相等,所以在判定两个直角三角形全等时,要注意到这两个三角形中已经具备一对对应角相等的条件了,只需找另外两个条件即可,而HL定理是直角三角形独有的,所以运用HL定理时,一定要指出是直角三角形.
总 结
典题精讲
[易错题]如图,AB=BC,AB⊥BC于B,FC⊥CB于C,E为BC上一点,BE=FC,试说明:AE⊥BF .
解:∵AB⊥BC于B,FC⊥CB于C,
∴∠ABE=∠BCF=90°.
∵AB=BC,BE=CF,
∴△ABE≌△BCF(SAS),∴∠A=∠FBC .
∵∠A+∠AEB=90°,
∴∠FBC+∠AEB=90°,∠BED=90°,
∴AE⊥BF .
典题精讲
如图,在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
典题精讲
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当的条件: _______________________________,
使△AEH≌△CEB.
AH=CB(或EH=EB或AE=CE)
学以致用
小试牛刀
1.______和一条________分别相等的两个直角三角形全等,可以简写成“_______________”或“____”.
斜边
直角边
斜边、直角边
HL
2.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加 一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是______________________.
AB=DC(答案不唯一)
小试牛刀
3.如图,在△ABC中,AB=AC,若AD⊥BC,则可直接
判定△ABD和△ACD全等的方法是( )
A.SAS B.ASA C.SSS D.HL
D
4.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( )
A.4 cm B.5 cm
C.6 cm D.7 cm
C
小试牛刀
5.如图,H是△ABC的高AD,BE的交点,且DH=DC,
则下列结论:①BD=AD;②BC=AC;③BH=AC;
④CE=CD中,正确的有( )
A.1个 B.2个 C.3个 D.4个
B
6.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=134°,则∠EDF的度数为( )
A.44° B.36°
C.46° D.34°
A
小试牛刀
7.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证△ACB≌△BDA;
证明:∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形.
∴Rt△ACB≌Rt△BDA(HL).
在Rt△ACB和Rt△BDA中,
(2)若∠ABC=35°,则∠CAO=______.
20°
小试牛刀
8.已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N .
(1) 如图①,求证AE=BD;
证明:∵△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE .
∴△ACE≌△BCD(SAS). ∴AE=BD .
在△ACE和△BCD中,
小试牛刀
(2)如图②,若AC=DC,在不添加任何辅助线的情况下,请直接写出图②中四对全等的直角三角形.
解:△ACB≌△DCE,
△EMC≌△BNC,
△AON≌△DOM,
△AOB≌△DOE .
课堂小结
课堂小结
判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边是锐角的对边,用“AAS”判定;②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.4 直角三角形全等的判定
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下课后,小强和小星为“边边角”是否成立展开了争论,小强认为,对于两个三角形,有“边、边、角”对应相等,这两个三角形不全等.小星则画了如下的两个直角三角形(如图).其中∠C=∠C′=90°,AB=A′B′,BC=B′C′,将它们从纸片上剪下来,发现它们重合,于是断定“边、边、角”对应相等的条件能判定两个三角形全等,你认为他说的有道理吗?
新课精讲
探索新知
1
知识点
判定两直角三角形全等的方法:斜边、直角边
我们已经知道,三边对应相等的两个三角形全等 .
由勾股定理可知,两边对应相等的两个直角三角形,其第三边一定相等 . 从而,这两个直角三角形一定全等 . 因此,斜边和一条直角边对应相等的两个直角三角形全等 . 证明过程如下:
探索新知
已知:如图,在△ABC和△A′B′C′中,∠C=∠ C′=90°,AB = A′B′ ,AC= A′C′ . 求证:△ABC≌△A′B′C′ .
证明:在△ABC和△A′B′C′中,
∵∠C=90°,∠C′=90°,
∴BC2=AB2-AC2,
B′C′2=A′B′2-A′C′2(勾股定理).
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS) .
探索新知
归 纳
斜边和直角边对应相等的两个直角三角形全等 .
这个定理可以简写为“斜边、直角边”或“HL”.
探索新知
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C, D,且PC=PD . 求证:点P在∠AOB的平分线上 .
例1
证明:如图,作射线OP.
∵PC⊥OA, PD⊥OB,∴∠PCO=∠PDO=90°.
在 Rt△OPC 和 Rt△OPD 中,
∴Rt△OFC≌Rt△OPD( HL).
∴∠POA=∠POB.∴OP是∠AOB的平分线,即点P在∠AOB的平分线上 .
探索新知
总 结
应用“HL”判定两个直角三角形全等,书写时,必须强调是直角三角形.
典题精讲
如图,在△ABC中,AB=CB,∠ABC= 90°,F为AB延长线上一
点,点E在BC上,且AE=CF . 求证: Rt△ABE≌Rt△CBF .
证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90° .
在Rt△ABE和Rt△CBF中,
∵
∴Rt△ABE≌Rt△CBF(HL).
典题精讲
2 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ ABC与Rt△ABD全等.以下给出的条件正确的是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3 下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.两条边对应相等
A
D
证明:在Rt△ABC和Rt△ABD中,
∵AC=AD,AB=AB,
∴Rt△ABC≌Rt△ABD(HL),∴∠CAB=∠DAB .
在△AEC和△AED中,∵AC=AD,∠CAE=∠DAE,AE=AE,
∴△AEC≌△AED(SAS), ∴CE=DE .
探索新知
2
知识点
直角三角形全等的综合判定
例2 [探究题] 如图所示,已知∠ACB=∠ADB=90°,
AC=AD,E是AB上任意一点.求证:CE=DE .
探索新知
直角三角形是一类特殊的三角形,它具有一般三角形的所有性质,因此,判定两个直角三角形全等时,完全可以采用一般三角形全等的判定方法.由于直角三角形中有一个直角,而直角都相等,所以在判定两个直角三角形全等时,要注意到这两个三角形中已经具备一对对应角相等的条件了,只需找另外两个条件即可,而HL定理是直角三角形独有的,所以运用HL定理时,一定要指出是直角三角形.
总 结
典题精讲
[易错题]如图,AB=BC,AB⊥BC于B,FC⊥CB于C,E为BC上一点,BE=FC,试说明:AE⊥BF .
解:∵AB⊥BC于B,FC⊥CB于C,
∴∠ABE=∠BCF=90°.
∵AB=BC,BE=CF,
∴△ABE≌△BCF(SAS),∴∠A=∠FBC .
∵∠A+∠AEB=90°,
∴∠FBC+∠AEB=90°,∠BED=90°,
∴AE⊥BF .
典题精讲
如图,在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
典题精讲
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当的条件: _______________________________,
使△AEH≌△CEB.
AH=CB(或EH=EB或AE=CE)
学以致用
小试牛刀
1.______和一条________分别相等的两个直角三角形全等,可以简写成“_______________”或“____”.
斜边
直角边
斜边、直角边
HL
2.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加 一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是______________________.
AB=DC(答案不唯一)
小试牛刀
3.如图,在△ABC中,AB=AC,若AD⊥BC,则可直接
判定△ABD和△ACD全等的方法是( )
A.SAS B.ASA C.SSS D.HL
D
4.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( )
A.4 cm B.5 cm
C.6 cm D.7 cm
C
小试牛刀
5.如图,H是△ABC的高AD,BE的交点,且DH=DC,
则下列结论:①BD=AD;②BC=AC;③BH=AC;
④CE=CD中,正确的有( )
A.1个 B.2个 C.3个 D.4个
B
6.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=134°,则∠EDF的度数为( )
A.44° B.36°
C.46° D.34°
A
小试牛刀
7.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证△ACB≌△BDA;
证明:∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形.
∴Rt△ACB≌Rt△BDA(HL).
在Rt△ACB和Rt△BDA中,
(2)若∠ABC=35°,则∠CAO=______.
20°
小试牛刀
8.已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N .
(1) 如图①,求证AE=BD;
证明:∵△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE .
∴△ACE≌△BCD(SAS). ∴AE=BD .
在△ACE和△BCD中,
小试牛刀
(2)如图②,若AC=DC,在不添加任何辅助线的情况下,请直接写出图②中四对全等的直角三角形.
解:△ACB≌△DCE,
△EMC≌△BNC,
△AON≌△DOM,
△AOB≌△DOE .
课堂小结
课堂小结
判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边是锐角的对边,用“AAS”判定;②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
