冀教版(新)八上-17.5 反证法【优质课件】
文档属性
| 名称 | 冀教版(新)八上-17.5 反证法【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
17.5 反证法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在证明一些命题为真命题时,一般用直接证明的方法,但有时用间接的证明方法可能更方便 . 反证法就是一种常用的间接证明方法 .
新课精讲
探索新知
1
知识点
反证法的意义
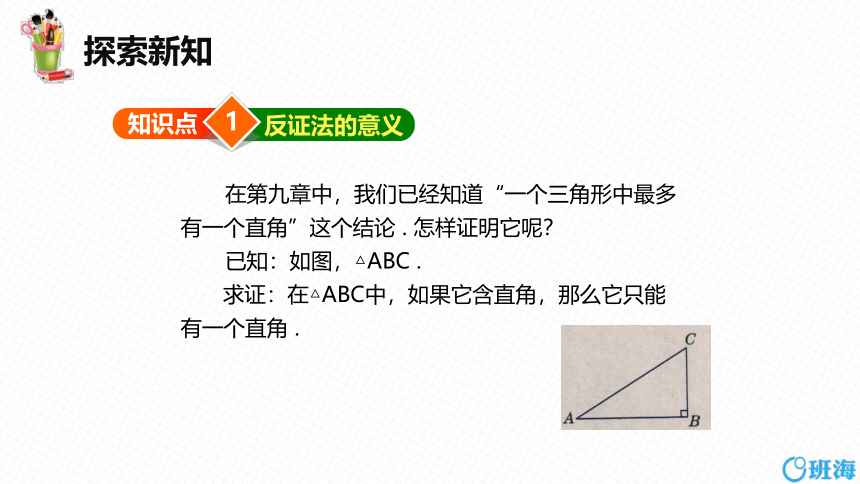
在第九章中,我们已经知道“一个三角形中最多
有一个直角”这个结论 . 怎样证明它呢?
已知:如图,△ABC .
求证:在△ABC中,如果它含直角,那么它只能
有一个直角 .
探索新知
证明:假设△ABC中有两个(或三个)直角,不妨设 ∠A=∠B =90°.
∵∠A+∠B=180°,
∴∠A+∠B+∠C >180°.
这与“三角形的内角和等于180°”相矛盾 .
因此,三角形有两个(或三个)直角的假设是不成立的 .
所以,如果三角形含直角,那么它只能有一个直角 .
探索新知
归 纳
上面的证明过程,是先假设原命题结论不正确,然后从这个假设出发,经过逐步推理论证,最后推出与学过的三角形内角和定理相矛盾的结果 . 因此,假设是错误的,原结论是正确的 .
这种证明命题的方法叫做反证法 . 反证法是一种间接证明的方法 .
探索新知
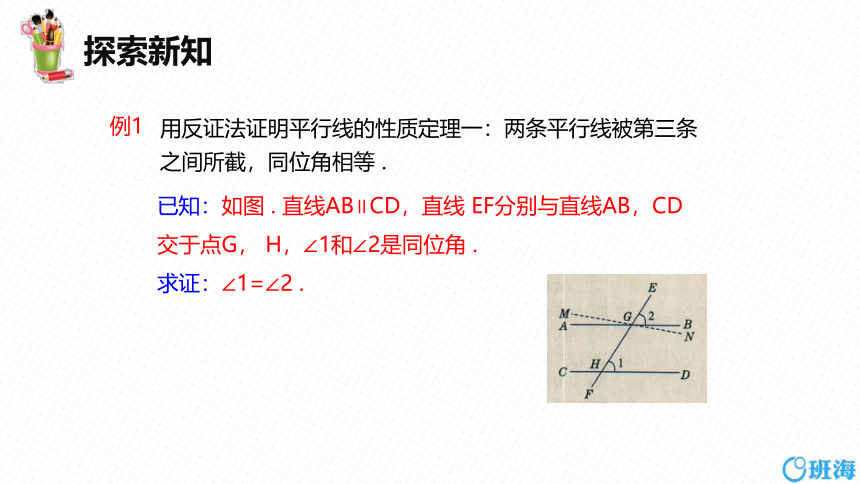
用反证法证明平行线的性质定理一:两条平行线被第三条之间所截,同位角相等 .
例1
已知:如图 . 直线AB∥CD,直线 EF分别与直线AB,CD交于点G, H,∠1和∠2是同位角 .
求证:∠1=∠2 .
探索新知
假设∠1≠∠2 .
过点G作直线MN,使得∠EGN =∠1 .
∴∠EGN=∠1,
∴ MN∥CD(基本事实) .
又∵AB∥CD(已知),
∴过点G,有两条不同的直线AB和MN都与直线CD平行 . 这与“经过已知直线外一点,有且只有一条直线和已知直线平行”相矛盾 .
∴∠1≠∠2的假设是不成立的 . 因此,∠1=∠2 .
证明:
探索新知
总 结
对于本题,要先写出已知、求证,然后运用反证法证明.
典题精讲
用反证法证明:等腰三角形的底角是锐角.
解:已知:在△ABC中,AB=AC .
求证:∠B和∠C都是锐角.
证明:假设等腰三角形ABC的底角∠B和∠C都不是锐角,则∠B≥90°,∠C≥90°,
所以∠B+∠C≥180° .
则该三角形的三个内角的和一定大于180°,
这与三角形的内角和定理相矛盾,故假设不成立,即∠B和∠C都是锐角.
所以等腰三角形的底角是锐角.
典题精讲
用反证法证明“在同一平面内,若a⊥c,b⊥c,则a∥b”,第一步应假设( )
A.a∥b B.a与b垂直
C.a与b不一定平行 D.a与b相交
3 用反证法证明命题“如果x>y,那么x3>y3”时,假设的内容应
是( )
A.x3=y3 B.x3<y3
C.x3<y3或x3=y3 D.x3<y3且x3=y2
D
C
探索新知
2
知识点
用反证法证明的步骤
用反证法证明一个命题是真命题的一般步骤是:
第一步,假设命题的结论不成立 .
第二步,从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,已证明的定理、性质或题设条件相矛盾的结果 .
第三步,由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的 .
探索新知
已知:如图,在 △ABC和△A′B′C′中,
∠C=∠C′ =90°,AB=A′B′=AC=A′C′,
求证:△ABC≌△A′B′C′.
用反证法证明直角三角形全等的“斜边、直角边”定理 .
例2
探索新知
假设△ABC与△A′B′C′不全等,即BC≠B′C′ .
不妨设BC<B′C′ . 如图 . 在B′C′上截取连接A′D .
在△ABC和△A′B′C′ 中,∵AC = A′C′,∠C = ∠C′,CB = C′D,
∴△ABC≌△A′DC′(SAS) . ∴AB = A′D(全等三角形的对应边相等) .
∴AB = A′B′ (已知),∴A′B′ = A′D(等量代换) .
∴∠B′ = ∠A′DB′(等边对等角) .
∴∠A′DB′ <90°(三角形的内角和定理),
证明:
即∠C′<∠A′DB′<90°(三角形的外角大于和它不相邻的内角).
这与∠C′=90°相矛盾 . 因此,BC≠B′C′的假设不成立,
即△ABC与△A′B′C′不全等的假设不成立 .所以,△ABC≌△A′B′C′.
探索新知
用反证法证明时,一定要得出矛盾,这种矛盾可以是与已知矛盾,也可以是与某个定义、公理、定理矛盾 .
总 结
典题精讲
用反证法证明在一个三角形中,不能有两个角是钝角.
解:已知:∠A,∠B,∠C是三角形ABC的三个内角.
求证:∠A,∠B,∠C中不能有两个钝角.
证明:假设∠A,∠B,∠C中有两个钝角,不妨
设∠A>90°,∠B>90°,则∠A+∠B+∠C>
180°,这与三角形的内角和定理相矛盾. 故 ∠A,
∠B均大于90°不成立.
所以,在一个三角形中不能有两个钝角.
典题精讲
2 用反证法证明一个命题是真命题的一般步骤是:
(1)第一步,假设命题的结论________.
(2)第二步,从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,已证明的定理、性质或题设条件__________的结果.
(3)第三步,由矛盾的结果,判定假设________,从而说明命题的结论是________.
不成立
相矛盾
不成立
正确的
典题精讲
用反证法证明:若a,b,c是不全为0的实数,且a+b+c=0,那么a,b,c这三个数中至少有一个负数.
证明:假设a,b,c都不是______,
∵a,b,c不全为0,
∴a,b,c中至少有一个为正数,
∴a+b+c______0,这与已知相________,
∴______________,原命题成立,
即a,b,c这三个数中至少有一个负数.
负数
>
矛盾
假设不成立
学以致用
小试牛刀
1 . 先假设原命题结论________,然后从这个假设出发,经过逐步推理论证,最后推出与学过的定理_______的结果,因此,假设是_______,原结论是________,这种证明命题的方法叫做反证法.
不正确
相矛盾
错误的
正确的
2 . 已知:如图,直线a,b被c所截,∠1,∠2是同位角,且∠1≠∠2,求证:a不平行b.
证明:假设________,则________,这与________
相矛盾,所以_________不成立,所以a不平行b.
a平行b
∠1=∠2
∠1≠∠2
a平行b
小试牛刀
3.用反证法证明一个三角形的三个内角中不能有两个钝角,第一步
应假设( )
A.三角形的三个内角中能有两个钝角
B.三角形的三个内角中能有两个直角
C.三角形的三个内角中能有两个锐角
D.不能确定
4.否定结论“至多有两个解”的说法中,正确的是( )
A.有一个解 B.有两个解
C.至少有三个解 D.至少有两个解
A
C
小试牛刀
5.用反证法证明:同一平面内,若一条直线与两条平行线的一条相交,
则必与另一条相交 .已知:同一平面内,l1∥l2,l1与l3相交于点A,
如图 . 求证:l3必与l2相交 .
A
l1
l2
l3
证明:假设l3与l2不相交,
则l3∥l2,∵l1∥l2,l3∥l2,
∴l1∥l3,这与已知l1与l3相交于点A相矛盾,
∴假设不成立 . 故l3必与l2相交 .
小试牛刀
6 . 用反证法证明一个三角形中不能有两个角是直角.
证明:
假设三角形的三个内角A、B、C中有两个直角,不妨设∠A=∠B=90°,
则A+B+C=90°+90°+C>180°,这与三角形内角和为180°相矛盾,∴∠A=∠B=90°不成立;
所以一个三角形中不能有两个直角.
小试牛刀
7 . 证明题:如图所示,在△ABC中,AB=AC,∠APB≠∠APC,
求证:PB≠PC.
证明:假设PB≠PC不成立,
则PB=PC,∠PBC=∠PCB;
又∵AB=AC,∴∠ABC=∠ACB;∴∠ABP=∠ACP;
∴△ABP≌△ACP,∴∠APB=∠APC;
与∠APB≠∠APC相矛盾.
因而PB=PC不成立,则PB≠PC.
课堂小结
课堂小结
用反证法证明时要明确“两点”:
1.用反证法证明时,否定的是命题的结论,而不是否定已知条件.
2.适合用反证法的命题类型:
(1)结论以否定形式出现的命题,如钝角三角形中不能有两个钝角;
(2)唯一性命题,如两条直线相交只有一个交点;
(3)结论以“至多”“至少”等形式叙述的命题,如一个凸多边形中至多有3个锐角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.5 反证法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在证明一些命题为真命题时,一般用直接证明的方法,但有时用间接的证明方法可能更方便 . 反证法就是一种常用的间接证明方法 .
新课精讲
探索新知
1
知识点
反证法的意义
在第九章中,我们已经知道“一个三角形中最多
有一个直角”这个结论 . 怎样证明它呢?
已知:如图,△ABC .
求证:在△ABC中,如果它含直角,那么它只能
有一个直角 .
探索新知
证明:假设△ABC中有两个(或三个)直角,不妨设 ∠A=∠B =90°.
∵∠A+∠B=180°,
∴∠A+∠B+∠C >180°.
这与“三角形的内角和等于180°”相矛盾 .
因此,三角形有两个(或三个)直角的假设是不成立的 .
所以,如果三角形含直角,那么它只能有一个直角 .
探索新知
归 纳
上面的证明过程,是先假设原命题结论不正确,然后从这个假设出发,经过逐步推理论证,最后推出与学过的三角形内角和定理相矛盾的结果 . 因此,假设是错误的,原结论是正确的 .
这种证明命题的方法叫做反证法 . 反证法是一种间接证明的方法 .
探索新知
用反证法证明平行线的性质定理一:两条平行线被第三条之间所截,同位角相等 .
例1
已知:如图 . 直线AB∥CD,直线 EF分别与直线AB,CD交于点G, H,∠1和∠2是同位角 .
求证:∠1=∠2 .
探索新知
假设∠1≠∠2 .
过点G作直线MN,使得∠EGN =∠1 .
∴∠EGN=∠1,
∴ MN∥CD(基本事实) .
又∵AB∥CD(已知),
∴过点G,有两条不同的直线AB和MN都与直线CD平行 . 这与“经过已知直线外一点,有且只有一条直线和已知直线平行”相矛盾 .
∴∠1≠∠2的假设是不成立的 . 因此,∠1=∠2 .
证明:
探索新知
总 结
对于本题,要先写出已知、求证,然后运用反证法证明.
典题精讲
用反证法证明:等腰三角形的底角是锐角.
解:已知:在△ABC中,AB=AC .
求证:∠B和∠C都是锐角.
证明:假设等腰三角形ABC的底角∠B和∠C都不是锐角,则∠B≥90°,∠C≥90°,
所以∠B+∠C≥180° .
则该三角形的三个内角的和一定大于180°,
这与三角形的内角和定理相矛盾,故假设不成立,即∠B和∠C都是锐角.
所以等腰三角形的底角是锐角.
典题精讲
用反证法证明“在同一平面内,若a⊥c,b⊥c,则a∥b”,第一步应假设( )
A.a∥b B.a与b垂直
C.a与b不一定平行 D.a与b相交
3 用反证法证明命题“如果x>y,那么x3>y3”时,假设的内容应
是( )
A.x3=y3 B.x3<y3
C.x3<y3或x3=y3 D.x3<y3且x3=y2
D
C
探索新知
2
知识点
用反证法证明的步骤
用反证法证明一个命题是真命题的一般步骤是:
第一步,假设命题的结论不成立 .
第二步,从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,已证明的定理、性质或题设条件相矛盾的结果 .
第三步,由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的 .
探索新知
已知:如图,在 △ABC和△A′B′C′中,
∠C=∠C′ =90°,AB=A′B′=AC=A′C′,
求证:△ABC≌△A′B′C′.
用反证法证明直角三角形全等的“斜边、直角边”定理 .
例2
探索新知
假设△ABC与△A′B′C′不全等,即BC≠B′C′ .
不妨设BC<B′C′ . 如图 . 在B′C′上截取连接A′D .
在△ABC和△A′B′C′ 中,∵AC = A′C′,∠C = ∠C′,CB = C′D,
∴△ABC≌△A′DC′(SAS) . ∴AB = A′D(全等三角形的对应边相等) .
∴AB = A′B′ (已知),∴A′B′ = A′D(等量代换) .
∴∠B′ = ∠A′DB′(等边对等角) .
∴∠A′DB′ <90°(三角形的内角和定理),
证明:
即∠C′<∠A′DB′<90°(三角形的外角大于和它不相邻的内角).
这与∠C′=90°相矛盾 . 因此,BC≠B′C′的假设不成立,
即△ABC与△A′B′C′不全等的假设不成立 .所以,△ABC≌△A′B′C′.
探索新知
用反证法证明时,一定要得出矛盾,这种矛盾可以是与已知矛盾,也可以是与某个定义、公理、定理矛盾 .
总 结
典题精讲
用反证法证明在一个三角形中,不能有两个角是钝角.
解:已知:∠A,∠B,∠C是三角形ABC的三个内角.
求证:∠A,∠B,∠C中不能有两个钝角.
证明:假设∠A,∠B,∠C中有两个钝角,不妨
设∠A>90°,∠B>90°,则∠A+∠B+∠C>
180°,这与三角形的内角和定理相矛盾. 故 ∠A,
∠B均大于90°不成立.
所以,在一个三角形中不能有两个钝角.
典题精讲
2 用反证法证明一个命题是真命题的一般步骤是:
(1)第一步,假设命题的结论________.
(2)第二步,从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实,已证明的定理、性质或题设条件__________的结果.
(3)第三步,由矛盾的结果,判定假设________,从而说明命题的结论是________.
不成立
相矛盾
不成立
正确的
典题精讲
用反证法证明:若a,b,c是不全为0的实数,且a+b+c=0,那么a,b,c这三个数中至少有一个负数.
证明:假设a,b,c都不是______,
∵a,b,c不全为0,
∴a,b,c中至少有一个为正数,
∴a+b+c______0,这与已知相________,
∴______________,原命题成立,
即a,b,c这三个数中至少有一个负数.
负数
>
矛盾
假设不成立
学以致用
小试牛刀
1 . 先假设原命题结论________,然后从这个假设出发,经过逐步推理论证,最后推出与学过的定理_______的结果,因此,假设是_______,原结论是________,这种证明命题的方法叫做反证法.
不正确
相矛盾
错误的
正确的
2 . 已知:如图,直线a,b被c所截,∠1,∠2是同位角,且∠1≠∠2,求证:a不平行b.
证明:假设________,则________,这与________
相矛盾,所以_________不成立,所以a不平行b.
a平行b
∠1=∠2
∠1≠∠2
a平行b
小试牛刀
3.用反证法证明一个三角形的三个内角中不能有两个钝角,第一步
应假设( )
A.三角形的三个内角中能有两个钝角
B.三角形的三个内角中能有两个直角
C.三角形的三个内角中能有两个锐角
D.不能确定
4.否定结论“至多有两个解”的说法中,正确的是( )
A.有一个解 B.有两个解
C.至少有三个解 D.至少有两个解
A
C
小试牛刀
5.用反证法证明:同一平面内,若一条直线与两条平行线的一条相交,
则必与另一条相交 .已知:同一平面内,l1∥l2,l1与l3相交于点A,
如图 . 求证:l3必与l2相交 .
A
l1
l2
l3
证明:假设l3与l2不相交,
则l3∥l2,∵l1∥l2,l3∥l2,
∴l1∥l3,这与已知l1与l3相交于点A相矛盾,
∴假设不成立 . 故l3必与l2相交 .
小试牛刀
6 . 用反证法证明一个三角形中不能有两个角是直角.
证明:
假设三角形的三个内角A、B、C中有两个直角,不妨设∠A=∠B=90°,
则A+B+C=90°+90°+C>180°,这与三角形内角和为180°相矛盾,∴∠A=∠B=90°不成立;
所以一个三角形中不能有两个直角.
小试牛刀
7 . 证明题:如图所示,在△ABC中,AB=AC,∠APB≠∠APC,
求证:PB≠PC.
证明:假设PB≠PC不成立,
则PB=PC,∠PBC=∠PCB;
又∵AB=AC,∴∠ABC=∠ACB;∴∠ABP=∠ACP;
∴△ABP≌△ACP,∴∠APB=∠APC;
与∠APB≠∠APC相矛盾.
因而PB=PC不成立,则PB≠PC.
课堂小结
课堂小结
用反证法证明时要明确“两点”:
1.用反证法证明时,否定的是命题的结论,而不是否定已知条件.
2.适合用反证法的命题类型:
(1)结论以否定形式出现的命题,如钝角三角形中不能有两个钝角;
(2)唯一性命题,如两条直线相交只有一个交点;
(3)结论以“至多”“至少”等形式叙述的命题,如一个凸多边形中至多有3个锐角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
