冀教版(新)八上-16.3 角的平分线【优质教案】
文档属性
| 名称 | 冀教版(新)八上-16.3 角的平分线【优质教案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览



文档简介
班海数学精批——一本可精细批改的教辅
16.3 角的平分线
16.3.1 角的平分线的性质
学习目标
1.经历角的平分线性质的发现过程,初步掌握角的平分线的性质.
2.通过测量操作,发现角的平分线的性质定理
3.能运用角的平分线性质和判定解决简单的几何问题.
学习重点:掌握角的平分线的性质和判定.
学习难点:角的平分线的性质和判定的应用
学法指导:观察思考,动手操作,合作探究
学习过程
一、学前准备
1.什么是角的平分线?怎样画一个角的平分线?
2. 有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?
二、合作探究
探究1.
(1)从上面对平分角的仪器的探究中,可以得出作已知角的平分线的方法。已知什么?求作什么?
(2)把简易平分角的仪器放在角的两边.且平分角的仪器两边相等,从几何角度怎么画
(3) 简易平分角的仪器BC=DC,从几何角度如何画
(4)OC与简易平分角的仪器中,AE是同一条射线吗
(5)你能说明OC是∠AOB的平分线吗
探究2.
在角的平分线OC上任意找一点P,过P点分别作OA、OB的垂线交OA、O于M、N, PM、PN的长度是∠AOB的平分线上一点到∠AOB两边的距离.
(1) 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
PM PN
第一次
第二次
第三次
观察测量结果,猜想线段PD与PE的大小关系,写出结论:____________
(2)你能归纳角的平分线的性质吗
(3)你能用三角形全等证明这个性质吗
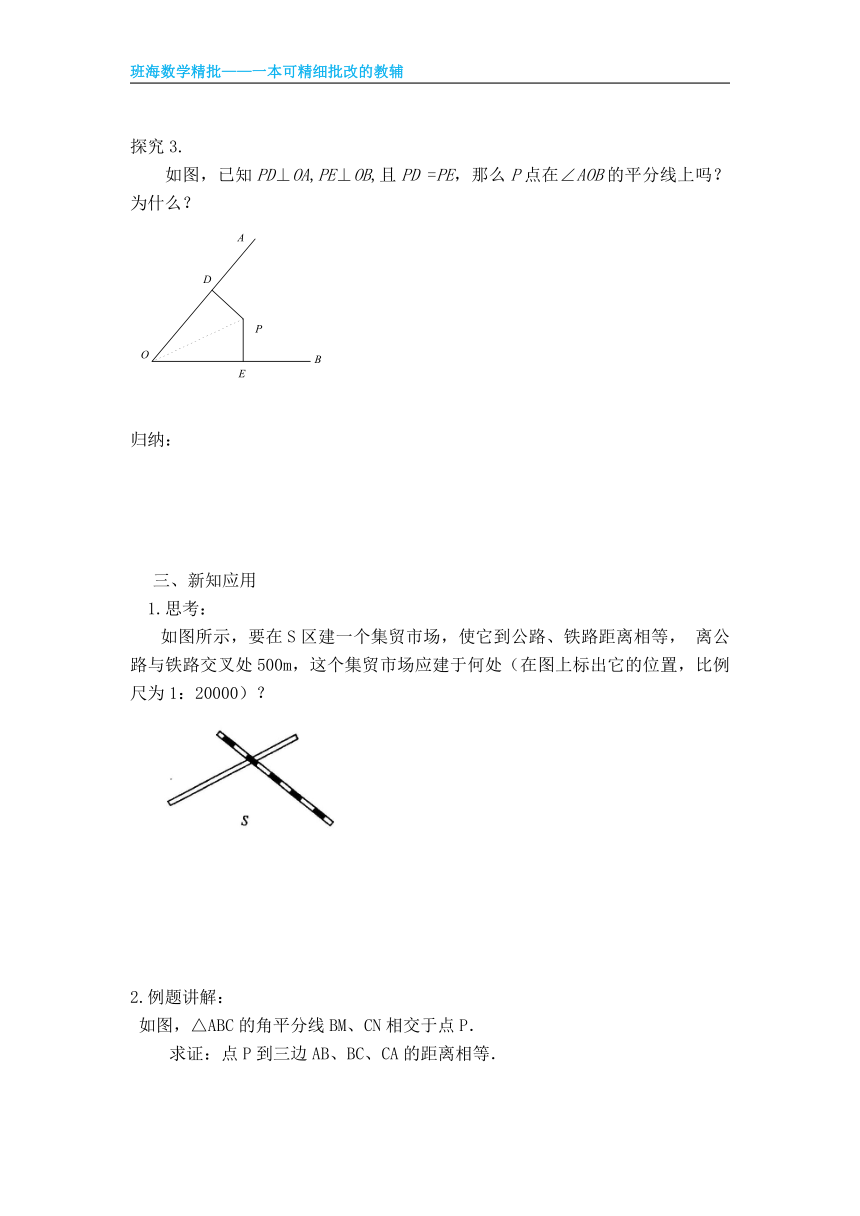
探究3.
如图,已知PD⊥OA,PE⊥OB,且PD =PE,那么P点在∠AOB的平分线上吗?为什么?
归纳:
三、新知应用
1.思考:
如图所示,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
2.例题讲解:
如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
分析:点P到AB、BC、CA的垂线段PD、PE、PF的长就是P点到三边的距离,也就是说要证:PD=PE=PF.而BM、CN分别是∠B、∠C的平分线,根据角平分线性质和等式的传递性可以解决这个问题.
四、巩固练习
五、课堂小结
1. 这节课你学到了哪些知识?
2. 你还有什么疑惑?
六、当堂清
1.在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5㎝,BD=3㎝,则点D到AB的距离为 。
2.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则M到OB的距离为 ㎝。
3.如图,∠A=90°,BD是△ABC的角平分线,AC=8㎝,DC=3DA,则点D到BC的距离为 。
4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
5.三角形中到三边距离相等的点是( )
A、三条边的垂直平分线的交点 B、三条高的交点
C、三条中线的交点 D、三条角平分线的交点
6.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,
求证:BE=CF
7.已知,如图BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于D,
求证:PM=PN
8.如图,某铁路MN与公路PQ相交于点O且交角为90°,某仓库G在A区,到公、铁路
距离相等,且到公路与铁路的相交点O的距离为200m。
在图上标出仓库G的位置。(比例尺:1:10000。用尺规作图,保留作图痕迹,不写作法)
16.3.2 角的平分线的判定
学习内容:通过独立思考和小组合作,能够证明几何命题。
学习目标:1、进一步熟练角平分线的画法,证明几何命题的步骤
2、进一步理解角平分线的性质及运用
学习重点:角平分线的性质及运用
学习难点:角平分线的性质的灵活运用
学习方法:探究、交流、练习
学习过程:
1、 课前巩固
1、 画出三角形三个内角的平分线
你发现了什么特点吗?
2、如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等
2、 学习新知
(1) 思考:
证明一个几何命题的一般步骤:
① ;
② ;
③ 。
(二)应用:
1、求证:到角的两边的距离相等的点在角的平分线上
2、如图所示,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
(1).集贸市场建于何处,和本节学的角平分线性质有关吗?用哪一个性质可以解决这个问题?
(2.比例尺为1:20000是什么意思?
三、基础练习
1.到角的两边距离相等的点在 上。
2.到三角形三边的距离相等的点是三角形( )
A.三条边上的高线的交点; B. 三个内角平分线的交点;
C.三条边上的中线的交点; D.以上结论都不对。
3.在△ABC中,∠C=90°,AD平分∠BAC,BC=8cm,BD=5cm,则D到AB的距离是 。
4.已知:AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,
求证 : ∠BAO=∠CAO
四、拓展延伸
已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上.
五、课堂小结
六、当堂检测
1、图中的直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( )
A.一处 B.两处
C.三处 D.四处
2.如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF,
求证:DF=EF
3. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
A
A
A
A
A
A
A
D
N
E
B
F
M
C
A
A
F
E
C
D
B
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
16.3 角的平分线
16.3.1 角的平分线的性质
学习目标
1.经历角的平分线性质的发现过程,初步掌握角的平分线的性质.
2.通过测量操作,发现角的平分线的性质定理
3.能运用角的平分线性质和判定解决简单的几何问题.
学习重点:掌握角的平分线的性质和判定.
学习难点:角的平分线的性质和判定的应用
学法指导:观察思考,动手操作,合作探究
学习过程
一、学前准备
1.什么是角的平分线?怎样画一个角的平分线?
2. 有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?
二、合作探究
探究1.
(1)从上面对平分角的仪器的探究中,可以得出作已知角的平分线的方法。已知什么?求作什么?
(2)把简易平分角的仪器放在角的两边.且平分角的仪器两边相等,从几何角度怎么画
(3) 简易平分角的仪器BC=DC,从几何角度如何画
(4)OC与简易平分角的仪器中,AE是同一条射线吗
(5)你能说明OC是∠AOB的平分线吗
探究2.
在角的平分线OC上任意找一点P,过P点分别作OA、OB的垂线交OA、O于M、N, PM、PN的长度是∠AOB的平分线上一点到∠AOB两边的距离.
(1) 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
PM PN
第一次
第二次
第三次
观察测量结果,猜想线段PD与PE的大小关系,写出结论:____________
(2)你能归纳角的平分线的性质吗
(3)你能用三角形全等证明这个性质吗
探究3.
如图,已知PD⊥OA,PE⊥OB,且PD =PE,那么P点在∠AOB的平分线上吗?为什么?
归纳:
三、新知应用
1.思考:
如图所示,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
2.例题讲解:
如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
分析:点P到AB、BC、CA的垂线段PD、PE、PF的长就是P点到三边的距离,也就是说要证:PD=PE=PF.而BM、CN分别是∠B、∠C的平分线,根据角平分线性质和等式的传递性可以解决这个问题.
四、巩固练习
五、课堂小结
1. 这节课你学到了哪些知识?
2. 你还有什么疑惑?
六、当堂清
1.在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5㎝,BD=3㎝,则点D到AB的距离为 。
2.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则M到OB的距离为 ㎝。
3.如图,∠A=90°,BD是△ABC的角平分线,AC=8㎝,DC=3DA,则点D到BC的距离为 。
4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
5.三角形中到三边距离相等的点是( )
A、三条边的垂直平分线的交点 B、三条高的交点
C、三条中线的交点 D、三条角平分线的交点
6.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,
求证:BE=CF
7.已知,如图BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于D,
求证:PM=PN
8.如图,某铁路MN与公路PQ相交于点O且交角为90°,某仓库G在A区,到公、铁路
距离相等,且到公路与铁路的相交点O的距离为200m。
在图上标出仓库G的位置。(比例尺:1:10000。用尺规作图,保留作图痕迹,不写作法)
16.3.2 角的平分线的判定
学习内容:通过独立思考和小组合作,能够证明几何命题。
学习目标:1、进一步熟练角平分线的画法,证明几何命题的步骤
2、进一步理解角平分线的性质及运用
学习重点:角平分线的性质及运用
学习难点:角平分线的性质的灵活运用
学习方法:探究、交流、练习
学习过程:
1、 课前巩固
1、 画出三角形三个内角的平分线
你发现了什么特点吗?
2、如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等
2、 学习新知
(1) 思考:
证明一个几何命题的一般步骤:
① ;
② ;
③ 。
(二)应用:
1、求证:到角的两边的距离相等的点在角的平分线上
2、如图所示,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
(1).集贸市场建于何处,和本节学的角平分线性质有关吗?用哪一个性质可以解决这个问题?
(2.比例尺为1:20000是什么意思?
三、基础练习
1.到角的两边距离相等的点在 上。
2.到三角形三边的距离相等的点是三角形( )
A.三条边上的高线的交点; B. 三个内角平分线的交点;
C.三条边上的中线的交点; D.以上结论都不对。
3.在△ABC中,∠C=90°,AD平分∠BAC,BC=8cm,BD=5cm,则D到AB的距离是 。
4.已知:AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,
求证 : ∠BAO=∠CAO
四、拓展延伸
已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上.
五、课堂小结
六、当堂检测
1、图中的直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( )
A.一处 B.两处
C.三处 D.四处
2.如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF,
求证:DF=EF
3. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:AD是△ABC的角平分线。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
A
A
A
A
A
A
A
D
N
E
B
F
M
C
A
A
F
E
C
D
B
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
