冀教版(新)八上-17.1 等腰三角形【优质教案】
文档属性
| 名称 | 冀教版(新)八上-17.1 等腰三角形【优质教案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 355.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:30 | ||
图片预览

文档简介
班海数学精批——一本可精细批改的教辅
17.1 等腰三角形
等腰三角形的性质
学习目标:1. 知道等腰三角形的有关概念,会画等腰三角形,能利用等腰三角形的性质进行有关的计算和证明.
2 . 经历等腰三角形学习过程,积累数学活动经验,体会数学的基本思想.
3.学会从数学角度发现问题和提出问题,获得分析问题和解决问题的一些基本方法,体会解决问题的多样性.
学习过程
一 .学习准备
1.已知等腰三角形的一边等于6cm,另一边等于8cm,则此三角形的周长为 .
2.等腰三角形中,一个角是40°,那么它的顶角度数为 .
3.等腰三角形腰为5cm,底边为6 cm,面积是 .
4.证明:等腰三角形两底角相等.(用规范的格式证明)
(通过上面的练习,说一说等腰三角形有那些性质)
二.学习探究
活动一
(1)如图1在等腰△ABC中,AB=AC=5,BC=6,P点为底边的中点,PD+PE= .
(2)如图2在等腰△ABC中,若P点为底边上任意一点,你认为PD+PE是定值吗?说明理由.
(3)如图3在等腰△ABC中,若P点为底边上任意一点,过C点做腰AB 上的高CF,你能发现PD,PE和CF存在什么数量关系,提出你的猜想并证明.
(4)如图4,若P点在BC的延长线上,那么PD,PE和CF的数量关系又有何变化?写出你的猜想并证明.
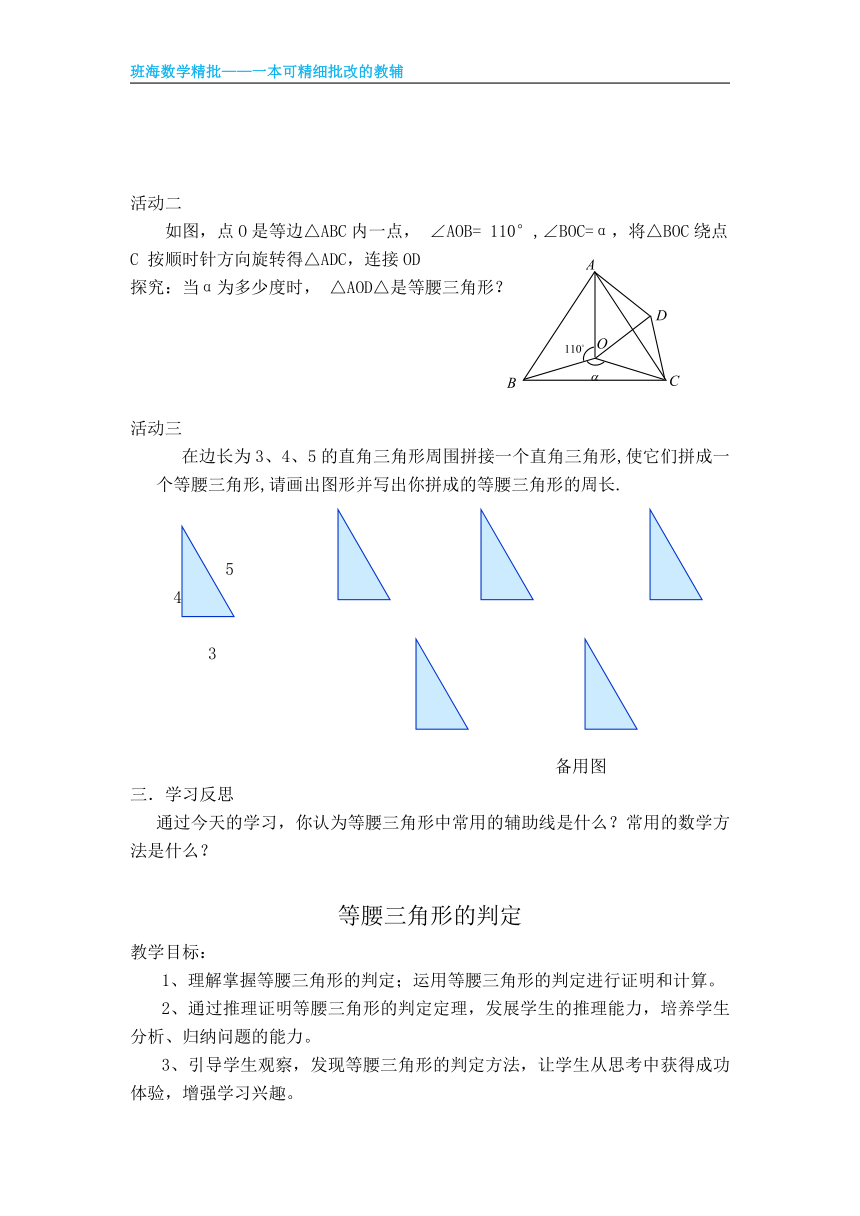
活动二
如图,点O是等边△ABC内一点, ∠AOB= 110°,∠BOC=α,将△BOC绕点C 按顺时针方向旋转得△ADC,连接OD
探究:当α为多少度时, △AOD△是等腰三角形?
活动三
在边长为3、4、5的直角三角形周围拼接一个直角三角形,使它们拼成一个等腰三角形,请画出图形并写出你拼成的等腰三角形的周长.
5
4
3
备用图
三.学习反思
通过今天的学习,你认为等腰三角形中常用的辅助线是什么?常用的数学方法是什么?
等腰三角形的判定
教学目标:
1、理解掌握等腰三角形的判定;运用等腰三角形的判定进行证明和计算。
2、通过推理证明等腰三角形的判定定理,发展学生的推理能力,培养学生分析、归纳问题的能力。
3、引导学生观察,发现等腰三角形的判定方法,让学生从思考中获得成功体验,增强学习兴趣。
教学重点:
等腰三角形的判定定理
教学难点:
等腰三角形的判定定理的证明
教学过程:
一、情境引入
如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B,如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
二、探究新知
1、思考:在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?你能证明吗?
已知:如图,在△ABC中,∠B=∠C
求证:AB=AC
引导学生作辅助线:作BC边上的高AD或作∠BAC的平分线AD,然后证明△ABD≌△ACD
2、归纳等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)
三、巩固新知
例1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
已知:如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC
求证:AB=AC
练习:
1、如图,∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形。
2、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD
四、应用新知
1、用尺规画一个底为,底边上的高为的等腰三角形(要求:写出已知和求作,保留作图痕迹)
已知:
求作:
2、如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于点D,DE∥AC交AB于点E,求证:AE=BE
五、课堂小结
1、通过这堂课的学习,你学会了哪几种判定等腰三角形的方法?
2、等腰三角形的性质与判定既有区别又有联系,你能总结一下吗?
六、作业
教材习题
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
A
B
C
D
O
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.1 等腰三角形
等腰三角形的性质
学习目标:1. 知道等腰三角形的有关概念,会画等腰三角形,能利用等腰三角形的性质进行有关的计算和证明.
2 . 经历等腰三角形学习过程,积累数学活动经验,体会数学的基本思想.
3.学会从数学角度发现问题和提出问题,获得分析问题和解决问题的一些基本方法,体会解决问题的多样性.
学习过程
一 .学习准备
1.已知等腰三角形的一边等于6cm,另一边等于8cm,则此三角形的周长为 .
2.等腰三角形中,一个角是40°,那么它的顶角度数为 .
3.等腰三角形腰为5cm,底边为6 cm,面积是 .
4.证明:等腰三角形两底角相等.(用规范的格式证明)
(通过上面的练习,说一说等腰三角形有那些性质)
二.学习探究
活动一
(1)如图1在等腰△ABC中,AB=AC=5,BC=6,P点为底边的中点,PD+PE= .
(2)如图2在等腰△ABC中,若P点为底边上任意一点,你认为PD+PE是定值吗?说明理由.
(3)如图3在等腰△ABC中,若P点为底边上任意一点,过C点做腰AB 上的高CF,你能发现PD,PE和CF存在什么数量关系,提出你的猜想并证明.
(4)如图4,若P点在BC的延长线上,那么PD,PE和CF的数量关系又有何变化?写出你的猜想并证明.
活动二
如图,点O是等边△ABC内一点, ∠AOB= 110°,∠BOC=α,将△BOC绕点C 按顺时针方向旋转得△ADC,连接OD
探究:当α为多少度时, △AOD△是等腰三角形?
活动三
在边长为3、4、5的直角三角形周围拼接一个直角三角形,使它们拼成一个等腰三角形,请画出图形并写出你拼成的等腰三角形的周长.
5
4
3
备用图
三.学习反思
通过今天的学习,你认为等腰三角形中常用的辅助线是什么?常用的数学方法是什么?
等腰三角形的判定
教学目标:
1、理解掌握等腰三角形的判定;运用等腰三角形的判定进行证明和计算。
2、通过推理证明等腰三角形的判定定理,发展学生的推理能力,培养学生分析、归纳问题的能力。
3、引导学生观察,发现等腰三角形的判定方法,让学生从思考中获得成功体验,增强学习兴趣。
教学重点:
等腰三角形的判定定理
教学难点:
等腰三角形的判定定理的证明
教学过程:
一、情境引入
如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B,如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
二、探究新知
1、思考:在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?你能证明吗?
已知:如图,在△ABC中,∠B=∠C
求证:AB=AC
引导学生作辅助线:作BC边上的高AD或作∠BAC的平分线AD,然后证明△ABD≌△ACD
2、归纳等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)
三、巩固新知
例1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
已知:如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC
求证:AB=AC
练习:
1、如图,∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形。
2、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD
四、应用新知
1、用尺规画一个底为,底边上的高为的等腰三角形(要求:写出已知和求作,保留作图痕迹)
已知:
求作:
2、如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于点D,DE∥AC交AB于点E,求证:AE=BE
五、课堂小结
1、通过这堂课的学习,你学会了哪几种判定等腰三角形的方法?
2、等腰三角形的性质与判定既有区别又有联系,你能总结一下吗?
六、作业
教材习题
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
A
B
C
D
O
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
