冀教版(新)八上-17.3 勾股定理【优质教案】
文档属性
| 名称 | 冀教版(新)八上-17.3 勾股定理【优质教案】 |  | |
| 格式 | doc | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:30 | ||
图片预览


文档简介
班海数学精批——一本可精细批改的教辅
17.3 勾股定理
认识勾股定理
【学习目标】
1、 经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推力意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。
2、 探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。
3、 【学习重点】了结勾股定理的由来,并能用它来解决一些简单的问题。
【学前准备】1、画一个直角三角形并测量三边的长。2、准备一张坐标纸
【自学探究】
阅读课本回答下列问题
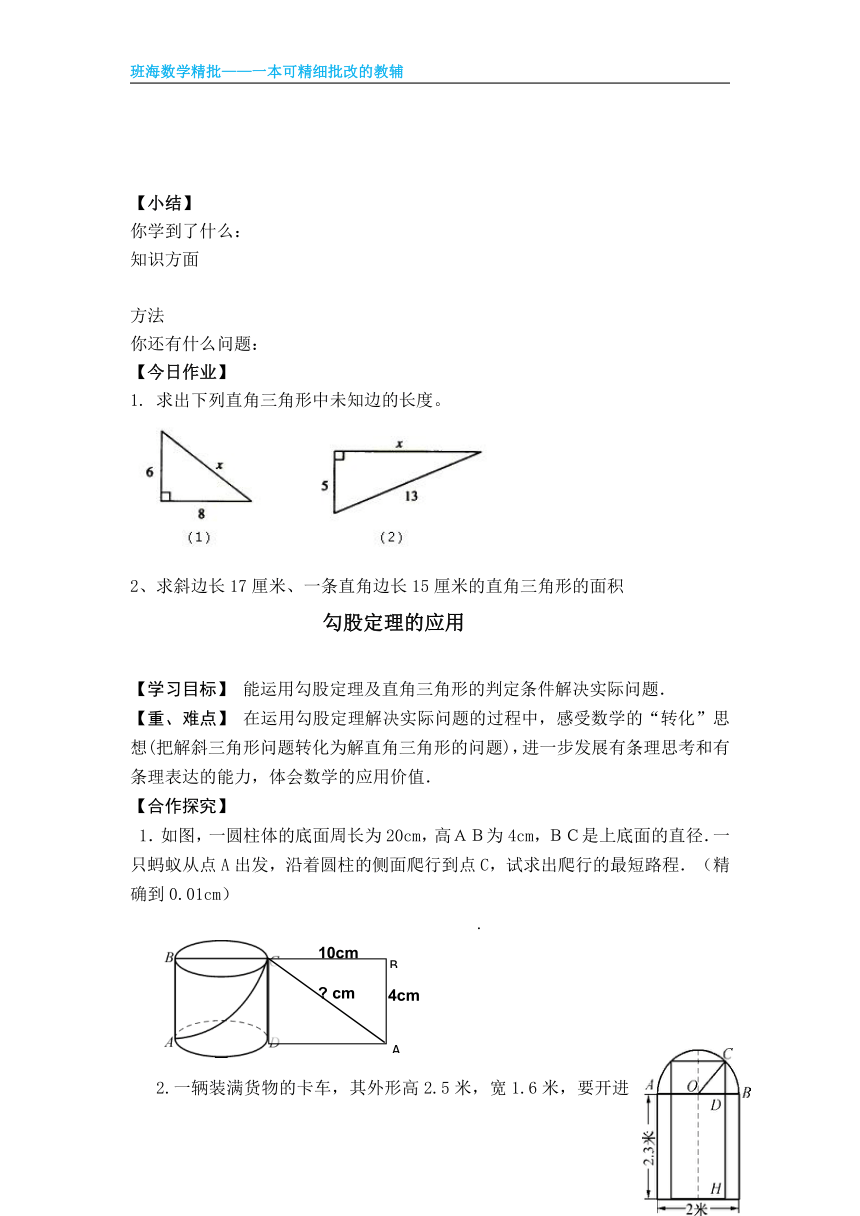
1、 直角三角形的两条直角边的长度分别为a=3㎝,b=4㎝和a=6㎝,b=8㎝。
11 你量出斜边c的长度。
(1) (2)
②进行有关的计算:(1)a2+b2=c2= (2) a2+b2=c2=
③得出结论:
2、思考:
(图中每个小方格代表一个单位面积)
(2)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中的呢?
(3)你能发现图1-1中三个正方形A,B,C围成的直角三角形三边的关系吗?
(4)你能发现课本图1-3中三个正方形A,B,C围成的直角三角形三边的关系吗?
(5)如果直角三角形的两直角边分别为1.6个单位长度和2.4个长度单位,上面所猜想的数量关系还成立吗?说明你的理由。
预习后你还有什么问题?最想和大家讨论交流的问题是什么?
【合作交流】
勾股定理:
例题:引例
【随堂练习】
1、练习
【巩固练习】
1.在△ABC中,∠C=90°,(l)若 a=5,b=12,则 c= (2)若c=41,a=9,则b=
2.等腰△ABC的腰长AB=10cm,底BC为16cm,则底边上的高为 ,面积为 。
3.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为()
A.42 B.32 C.42或 32 D.37 或 33
4.一个长方体抽斗的长为24cm,宽为7cm,在抽斗里放铁条,铁条最长能是多少?
【小结】
你学到了什么:
知识方面
方法
你还有什么问题:
【今日作业】
1. 求出下列直角三角形中未知边的长度。
2、求斜边长17厘米、一条直角边长15厘米的直角三角形的面积
勾股定理的应用
【学习目标】 能运用勾股定理及直角三角形的判定条件解决实际问题.
【重、难点】 在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.
【合作探究】
1.如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
.
2.一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如左图的某工厂,问这辆卡车能否通过该工厂的厂门
【课堂展示】
1.如图,在长、宽都是3,高是8的长方体纸箱的外部,一只蚂蚁从顶点A沿纸箱表面爬到顶点B处,求它所行的最短路线的长。
2.如图,一块草坪的形状为四边形ABCD,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.求这块草坪的面积.
3.如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设一拖拉机在公路MN上沿PN方向行驶,周围100米以内会受到噪声的影响,那么学校是否会受到噪声的影响 说明理由,若受影响,已知拖拉机的速度为18千米/时,则学校受影响的时间有多长
【自学测评】
1.在△ABC中,∠A: ∠B: ∠C=1:2:3,则BC:AC:AB=_________
2.甲、乙两人同时从同一地点出发,甲往东走了4km,乙往南走了6km,这时甲、乙两人相距__________km.
3.在△ABC中,AB=AC=4cm, ∠A: ∠B=2:5,过点C作△ABC的高CD,与AB交于D点,则CD=_______
4.如果梯子的底端建筑物有5m,15m长的梯子可达到该建筑物的高度大约是( )
A.13m B.14m C 15m D. 16 m
5.如图所示,在长方形纸片ABCD中,AD=4cm,AB=14cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长。
6.如图所示,在△ABC中,∠C=90°,CD⊥AB,垂足为D,BC=5cm,DC=4cm,求AC,AB的长。
勾股定理的逆定理
一、自学导航:
认真学习课本
★我们需要弄清:
① 互逆命题:如果两个命题的 和 正好相反,我们就把这样的两个命题叫做互逆命题。如果把其中一个叫做 ,那么另一个叫做它的 。
——你觉得这个“逆”字体现在哪里呢?
试一试:写出以下命题的逆命题。
(1)同旁内角互补,两条直线平行。
(2)如果两个实数相等,那么这两个实数的平方相等。
② 勾股定理的逆命题是:
。
事实上,古埃及人用结绳法构造直角三角形就是基于这样一种猜想。通过证明,我们发现这个命题是 (填是否正确)。它也是一个定理,我们把它叫做勾股定理的逆定理。
现在我们来回顾一下勾股定理逆定理的证明:
证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
① 请你自己画出图形并结合该图形写出已知条件和求证的结论:
② 请你尝试证明勾股定理逆定理的正确性。
请记住“我”——原命题成立其逆命题不一定成立。 ——你能举几个例子吗?
③ 根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条 边的平方和是否等于 的平方。 ——你知道为什么吗?
★ 小试牛刀:
1、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?
(1)a=,b=,c= (2)a=5,b=7,c=9
(3)a=2,b=,c= (4)a=5,b=,c=1
2、说一说你对例2的理解。
3、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,a=n2-1,b=2n,c=n2+1(n>1)
求证:∠C=90°。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
(1)观察图1-1。 A的面积是__________个单位面积;
B的面积是__________个单位面积;
C的面积是__________个单位面积。
B
A
10cm
4cm
cm
A
B
C
D
C/
A
C
B
D
导学提示区:
你觉得三边长分别为3、4、5的三角形和两直角边长分别为3、4的直角三角形之间有什么关系?这个关系能帮助你说明前一个三角形的形状特征码?
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.3 勾股定理
认识勾股定理
【学习目标】
1、 经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推力意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。
2、 探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。
3、 【学习重点】了结勾股定理的由来,并能用它来解决一些简单的问题。
【学前准备】1、画一个直角三角形并测量三边的长。2、准备一张坐标纸
【自学探究】
阅读课本回答下列问题
1、 直角三角形的两条直角边的长度分别为a=3㎝,b=4㎝和a=6㎝,b=8㎝。
11 你量出斜边c的长度。
(1) (2)
②进行有关的计算:(1)a2+b2=c2= (2) a2+b2=c2=
③得出结论:
2、思考:
(图中每个小方格代表一个单位面积)
(2)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?图1-2中的呢?
(3)你能发现图1-1中三个正方形A,B,C围成的直角三角形三边的关系吗?
(4)你能发现课本图1-3中三个正方形A,B,C围成的直角三角形三边的关系吗?
(5)如果直角三角形的两直角边分别为1.6个单位长度和2.4个长度单位,上面所猜想的数量关系还成立吗?说明你的理由。
预习后你还有什么问题?最想和大家讨论交流的问题是什么?
【合作交流】
勾股定理:
例题:引例
【随堂练习】
1、练习
【巩固练习】
1.在△ABC中,∠C=90°,(l)若 a=5,b=12,则 c= (2)若c=41,a=9,则b=
2.等腰△ABC的腰长AB=10cm,底BC为16cm,则底边上的高为 ,面积为 。
3.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为()
A.42 B.32 C.42或 32 D.37 或 33
4.一个长方体抽斗的长为24cm,宽为7cm,在抽斗里放铁条,铁条最长能是多少?
【小结】
你学到了什么:
知识方面
方法
你还有什么问题:
【今日作业】
1. 求出下列直角三角形中未知边的长度。
2、求斜边长17厘米、一条直角边长15厘米的直角三角形的面积
勾股定理的应用
【学习目标】 能运用勾股定理及直角三角形的判定条件解决实际问题.
【重、难点】 在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.
【合作探究】
1.如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
.
2.一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如左图的某工厂,问这辆卡车能否通过该工厂的厂门
【课堂展示】
1.如图,在长、宽都是3,高是8的长方体纸箱的外部,一只蚂蚁从顶点A沿纸箱表面爬到顶点B处,求它所行的最短路线的长。
2.如图,一块草坪的形状为四边形ABCD,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.求这块草坪的面积.
3.如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设一拖拉机在公路MN上沿PN方向行驶,周围100米以内会受到噪声的影响,那么学校是否会受到噪声的影响 说明理由,若受影响,已知拖拉机的速度为18千米/时,则学校受影响的时间有多长
【自学测评】
1.在△ABC中,∠A: ∠B: ∠C=1:2:3,则BC:AC:AB=_________
2.甲、乙两人同时从同一地点出发,甲往东走了4km,乙往南走了6km,这时甲、乙两人相距__________km.
3.在△ABC中,AB=AC=4cm, ∠A: ∠B=2:5,过点C作△ABC的高CD,与AB交于D点,则CD=_______
4.如果梯子的底端建筑物有5m,15m长的梯子可达到该建筑物的高度大约是( )
A.13m B.14m C 15m D. 16 m
5.如图所示,在长方形纸片ABCD中,AD=4cm,AB=14cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长。
6.如图所示,在△ABC中,∠C=90°,CD⊥AB,垂足为D,BC=5cm,DC=4cm,求AC,AB的长。
勾股定理的逆定理
一、自学导航:
认真学习课本
★我们需要弄清:
① 互逆命题:如果两个命题的 和 正好相反,我们就把这样的两个命题叫做互逆命题。如果把其中一个叫做 ,那么另一个叫做它的 。
——你觉得这个“逆”字体现在哪里呢?
试一试:写出以下命题的逆命题。
(1)同旁内角互补,两条直线平行。
(2)如果两个实数相等,那么这两个实数的平方相等。
② 勾股定理的逆命题是:
。
事实上,古埃及人用结绳法构造直角三角形就是基于这样一种猜想。通过证明,我们发现这个命题是 (填是否正确)。它也是一个定理,我们把它叫做勾股定理的逆定理。
现在我们来回顾一下勾股定理逆定理的证明:
证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
① 请你自己画出图形并结合该图形写出已知条件和求证的结论:
② 请你尝试证明勾股定理逆定理的正确性。
请记住“我”——原命题成立其逆命题不一定成立。 ——你能举几个例子吗?
③ 根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条 边的平方和是否等于 的平方。 ——你知道为什么吗?
★ 小试牛刀:
1、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?
(1)a=,b=,c= (2)a=5,b=7,c=9
(3)a=2,b=,c= (4)a=5,b=,c=1
2、说一说你对例2的理解。
3、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,a=n2-1,b=2n,c=n2+1(n>1)
求证:∠C=90°。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
(1)观察图1-1。 A的面积是__________个单位面积;
B的面积是__________个单位面积;
C的面积是__________个单位面积。
B
A
10cm
4cm
cm
A
B
C
D
C/
A
C
B
D
导学提示区:
你觉得三边长分别为3、4、5的三角形和两直角边长分别为3、4的直角三角形之间有什么关系?这个关系能帮助你说明前一个三角形的形状特征码?
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
