冀教版(新)八上-12.2 分式的乘除【优质教案】
文档属性
| 名称 | 冀教版(新)八上-12.2 分式的乘除【优质教案】 |  | |
| 格式 | doc | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:30 | ||
图片预览




文档简介
班海数学精批——一本可精细批改的教辅
12.2 分式的乘除
分式的乘法
学习目标:
1.理通过类比分数的乘法法则,探索分式的乘法法则并运用.
2.理通过类比整式的乘方法则,探索分式的乘方法则.
学习重点:分式的乘法法则.
学习难点:分式的乘法运算..
知识链接
×=_______;×=_______;
××=_______;×××=_______.
2一个长方体容器的容积为V,底面的长为a,宽为b,当容器的水占容积的时,求水的高为________ .
二、新知预习
3.我们已经熟悉分数的乘法运算,那么怎样进行分式的乘法运算呢?
类比分数的乘法运算,可知
分式的乘法法则:分式与分式相乘,用_________作为积的分子,_________作为积的分母.
NOTE:分式的运算结果要化为最简分式或整式.
4.类比: (ab)n=an bn ,那么
分式的乘方法则:分式的乘方就是分子、分母分别_________.
三、自学自测
1.计算等于( )
A. B. C. D.xy2
2计算下列各分式:
; (2).
四、我的疑惑
_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:分式的乘法
问题1:(1)·;(2)·.
【归纳总结】分子和分母都是单项式的分式的乘法,直接按“分子乘分子,分母乘分母”进行运算,其运算步骤为:(1)符号运算;(2)按分式的乘法法则运算;(3)各分式中的分子、分母都是多项式时,先因式分解,再约分.
【针对训练】
下列各式的计算结果中,是分式的是 ( )
①; ②; ③; ④.
A. ① B.①④ C. ②④ D.①③
问题2:先化简,再求值:·,其中x=,y=.
【归纳总结】根据分式乘法法则将代数式进行计算化简,再代入求值.
【针对训练】
先化简,再求值:,其中x=.
问题3:计算:(1);(2).
【归纳总结】根整式与分式相乘,可以将整式的分母看成是1,在根据分式的乘法法则进行计算.
【针对训练】
计算:(1);(2).
探究点2:分式的乘方
问题:下列运算结果不正确的是( )
A.()2=()2=
B.[-()2]3=-()6=-
C.[]3=()3=
D.(-)n=
【归纳总结】分式的乘方就是分子、分母分别乘方,最后化为最简分式.
【针对训练】
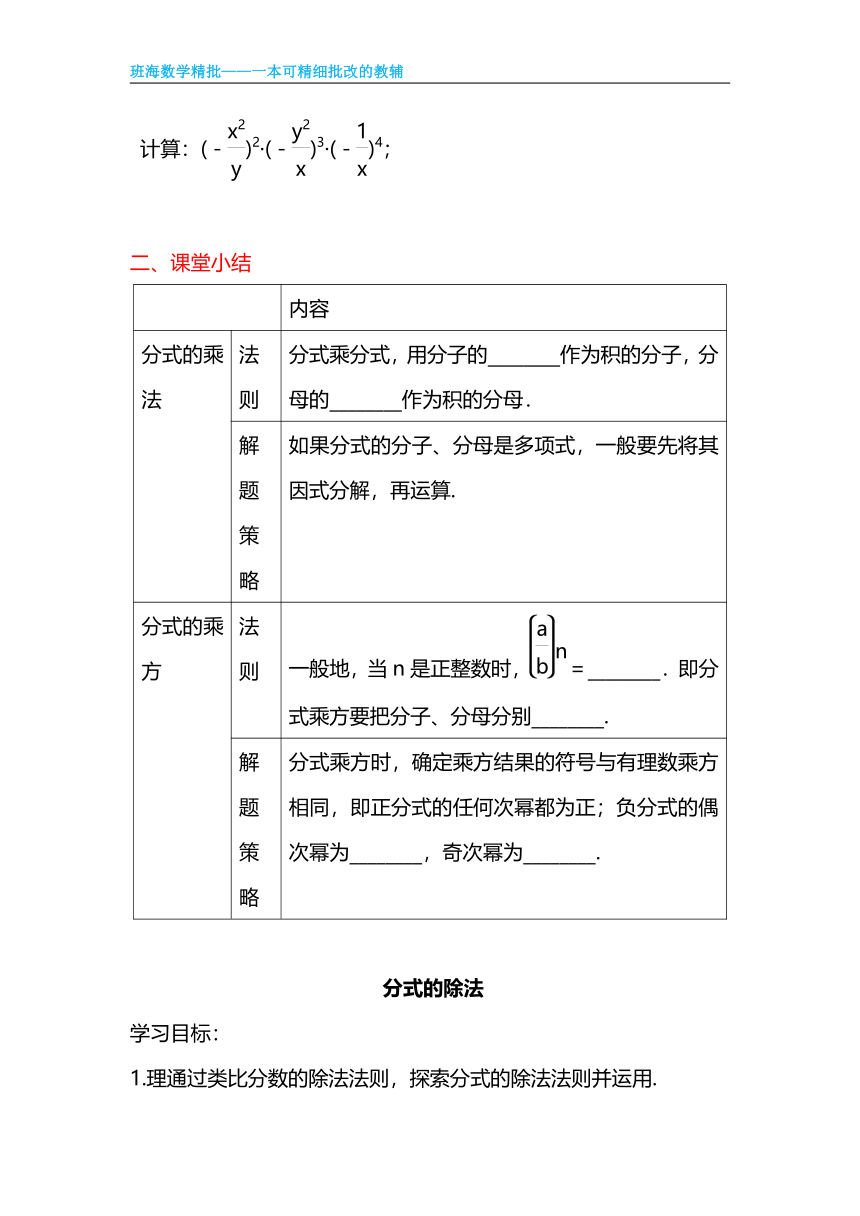
计算:(-)2·(-)3·(-)4;
二、课堂小结
内容
分式的乘法 法则 分式乘分式,用分子的________作为积的分子,分母的________作为积的分母.
解题策略 如果分式的分子、分母是多项式,一般要先将其因式分解,再运算.
分式的乘方 法则 一般地,当n是正整数时,=________.即分式乘方要把分子、分母分别________.
解题策略 分式乘方时,确定乘方结果的符号与有理数乘方相同,即正分式的任何次幂都为正;负分式的偶次幂为________,奇次幂为________.
分式的除法
学习目标:
1.理通过类比分数的除法法则,探索分式的除法法则并运用.
2.能够熟练的进行分式的乘除法混合运算.
学习重点:分式的除法法则.
学习难点:分式的乘除法运算..
知识链接
÷=____×____=____,÷=____×____=____.
大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的____________倍.
二、新知预习
3.我们已经熟悉分数的除法运算,那么怎样进行分式的除法运算呢?
类比分数的除法运算,可知
分式的除法法则:分式除以分式,把除式的分子与分母_________后,与被除式相乘.
由此可知,分式的除法运算时转化为分式的乘法运算进行的.
三、自学自测
1.计算的结果为( )
A. B.x2y C.-x2y D.-xy
2.计算:
; .
四、我的疑惑
_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:分式的除法
问题1:(1)-3xy÷;(2)(xy-x2)÷.
【归纳总结】先将除法变为乘法,再利用分式的乘法法则进行运算,做乘法运算时要注意先把分子、分母能因式分解的先分解,再约分.
【针对训练】
计算: .
问题2:先化简,再求值:÷,其中x=π+1.
【归纳总结】将除法转化为乘法后约分化简,然后代入求值.
【针对训练】
先化简,然后请你选择一个合适的x的值代入求值:.
问题3:若式子÷有意义,则x的取值范围是( )
x≠-2,x≠-4 B.x≠-2
C.x≠-2,x≠-3,x≠-4 D.x≠-2,x≠-3
【归纳总结】在分式的除法中,求字母的取值范围时要使被除式的分母不为0,同时还要使除式的分子、分母不为0.
【针对训练】
若代数式有意义,则x的取值范围是__________.
问题4:老王家种植两块正方形土地,边长分别为a米和b米(a≠b),老李家种植一块长方形土地,长为2a米,宽为b米.他们种的都是花生,并且总产量相同,试问老王家种植的花生单位面积产量是老李家种植的单位面积产量的多少倍?
【归纳总结】此题考查分式乘除运算的运用,注意理清题意,正确列式计算即可.
【针对训练】
通常购买同一品种的西瓜时,西瓜的质量越大,花费的钱越多,因此人们希望西瓜瓤占整个西瓜的比例越大越好.假如我们把西瓜都看成球形,并把西瓜瓤的密度看成是均匀的,西瓜的皮厚都是d,已知球的体积公式为V=πR3(其中R为球的半径),求:
西瓜瓤与整个西瓜的体积各是多少?
(2)西瓜瓤与整个西瓜的体积比是多少?
探究点2:分式的乘除混合运算
问题1:计算:·÷.
【归纳总结】分式乘除混合运算要注意以下几点:(1)利用分式除法法则把除法变成乘法;(2)进行约分,计算出结果.特别提醒:分式运算的最后结果是最简分式或整式.
【针对训练】
计算等于( )
A.a2 B. C. D.其他结果
问题2:计算:÷()2·.
【归纳总结】进行分式的乘除、乘方混合运算时,要严格按照运算顺序进行运算.先算乘方,再算乘除.注意结果一定要化成一个整式或最简分式的形式.
【针对训练】
计算:.
问题3:化简求值:()3÷()2·[]2,其中x=-,y=.
【归纳总结】先算乘方再算乘除,将原式化为最简形式,是解决此类问题的常用方法.
【针对训练】
化简求值:,其中x=-2.
二、课堂小结
内容
分式的除法 法则 分式除以分式,把除式中的分子、分母____________后,与被除式________.
解题策略 (1)当除式(或被除式)是整式时,可以看做分母是1的式子,然后按分式乘除法法则计算;(2)如果分式的分子、分母是多项式,一般要先将其因式分解,再运算.
乘除混合运算 先将除法统一成乘法,再按从左至右的顺序计算,若有括号要先算括号里面的.
乘方、乘除混合运算 先乘方、再乘除,含有多项式时,通常应先分解因式,能约分的要先约分,再计算.
分式化简求值的方法 (1)先把所给式子化简成最简分式或整式的形式,再将字母的值代入化简后的式子;(2)若题目中给出自主取数值代入求值时,要注意所选取的数值一定要使原分式有意义,即所取数值要使所给式子的分母及除数________0.
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
自主学习
合作探究
自主学习
合作探究
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
12.2 分式的乘除
分式的乘法
学习目标:
1.理通过类比分数的乘法法则,探索分式的乘法法则并运用.
2.理通过类比整式的乘方法则,探索分式的乘方法则.
学习重点:分式的乘法法则.
学习难点:分式的乘法运算..
知识链接
×=_______;×=_______;
××=_______;×××=_______.
2一个长方体容器的容积为V,底面的长为a,宽为b,当容器的水占容积的时,求水的高为________ .
二、新知预习
3.我们已经熟悉分数的乘法运算,那么怎样进行分式的乘法运算呢?
类比分数的乘法运算,可知
分式的乘法法则:分式与分式相乘,用_________作为积的分子,_________作为积的分母.
NOTE:分式的运算结果要化为最简分式或整式.
4.类比: (ab)n=an bn ,那么
分式的乘方法则:分式的乘方就是分子、分母分别_________.
三、自学自测
1.计算等于( )
A. B. C. D.xy2
2计算下列各分式:
; (2).
四、我的疑惑
_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:分式的乘法
问题1:(1)·;(2)·.
【归纳总结】分子和分母都是单项式的分式的乘法,直接按“分子乘分子,分母乘分母”进行运算,其运算步骤为:(1)符号运算;(2)按分式的乘法法则运算;(3)各分式中的分子、分母都是多项式时,先因式分解,再约分.
【针对训练】
下列各式的计算结果中,是分式的是 ( )
①; ②; ③; ④.
A. ① B.①④ C. ②④ D.①③
问题2:先化简,再求值:·,其中x=,y=.
【归纳总结】根据分式乘法法则将代数式进行计算化简,再代入求值.
【针对训练】
先化简,再求值:,其中x=.
问题3:计算:(1);(2).
【归纳总结】根整式与分式相乘,可以将整式的分母看成是1,在根据分式的乘法法则进行计算.
【针对训练】
计算:(1);(2).
探究点2:分式的乘方
问题:下列运算结果不正确的是( )
A.()2=()2=
B.[-()2]3=-()6=-
C.[]3=()3=
D.(-)n=
【归纳总结】分式的乘方就是分子、分母分别乘方,最后化为最简分式.
【针对训练】
计算:(-)2·(-)3·(-)4;
二、课堂小结
内容
分式的乘法 法则 分式乘分式,用分子的________作为积的分子,分母的________作为积的分母.
解题策略 如果分式的分子、分母是多项式,一般要先将其因式分解,再运算.
分式的乘方 法则 一般地,当n是正整数时,=________.即分式乘方要把分子、分母分别________.
解题策略 分式乘方时,确定乘方结果的符号与有理数乘方相同,即正分式的任何次幂都为正;负分式的偶次幂为________,奇次幂为________.
分式的除法
学习目标:
1.理通过类比分数的除法法则,探索分式的除法法则并运用.
2.能够熟练的进行分式的乘除法混合运算.
学习重点:分式的除法法则.
学习难点:分式的乘除法运算..
知识链接
÷=____×____=____,÷=____×____=____.
大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖拉机的工作效率是小拖拉机的工作效率的____________倍.
二、新知预习
3.我们已经熟悉分数的除法运算,那么怎样进行分式的除法运算呢?
类比分数的除法运算,可知
分式的除法法则:分式除以分式,把除式的分子与分母_________后,与被除式相乘.
由此可知,分式的除法运算时转化为分式的乘法运算进行的.
三、自学自测
1.计算的结果为( )
A. B.x2y C.-x2y D.-xy
2.计算:
; .
四、我的疑惑
_____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:分式的除法
问题1:(1)-3xy÷;(2)(xy-x2)÷.
【归纳总结】先将除法变为乘法,再利用分式的乘法法则进行运算,做乘法运算时要注意先把分子、分母能因式分解的先分解,再约分.
【针对训练】
计算: .
问题2:先化简,再求值:÷,其中x=π+1.
【归纳总结】将除法转化为乘法后约分化简,然后代入求值.
【针对训练】
先化简,然后请你选择一个合适的x的值代入求值:.
问题3:若式子÷有意义,则x的取值范围是( )
x≠-2,x≠-4 B.x≠-2
C.x≠-2,x≠-3,x≠-4 D.x≠-2,x≠-3
【归纳总结】在分式的除法中,求字母的取值范围时要使被除式的分母不为0,同时还要使除式的分子、分母不为0.
【针对训练】
若代数式有意义,则x的取值范围是__________.
问题4:老王家种植两块正方形土地,边长分别为a米和b米(a≠b),老李家种植一块长方形土地,长为2a米,宽为b米.他们种的都是花生,并且总产量相同,试问老王家种植的花生单位面积产量是老李家种植的单位面积产量的多少倍?
【归纳总结】此题考查分式乘除运算的运用,注意理清题意,正确列式计算即可.
【针对训练】
通常购买同一品种的西瓜时,西瓜的质量越大,花费的钱越多,因此人们希望西瓜瓤占整个西瓜的比例越大越好.假如我们把西瓜都看成球形,并把西瓜瓤的密度看成是均匀的,西瓜的皮厚都是d,已知球的体积公式为V=πR3(其中R为球的半径),求:
西瓜瓤与整个西瓜的体积各是多少?
(2)西瓜瓤与整个西瓜的体积比是多少?
探究点2:分式的乘除混合运算
问题1:计算:·÷.
【归纳总结】分式乘除混合运算要注意以下几点:(1)利用分式除法法则把除法变成乘法;(2)进行约分,计算出结果.特别提醒:分式运算的最后结果是最简分式或整式.
【针对训练】
计算等于( )
A.a2 B. C. D.其他结果
问题2:计算:÷()2·.
【归纳总结】进行分式的乘除、乘方混合运算时,要严格按照运算顺序进行运算.先算乘方,再算乘除.注意结果一定要化成一个整式或最简分式的形式.
【针对训练】
计算:.
问题3:化简求值:()3÷()2·[]2,其中x=-,y=.
【归纳总结】先算乘方再算乘除,将原式化为最简形式,是解决此类问题的常用方法.
【针对训练】
化简求值:,其中x=-2.
二、课堂小结
内容
分式的除法 法则 分式除以分式,把除式中的分子、分母____________后,与被除式________.
解题策略 (1)当除式(或被除式)是整式时,可以看做分母是1的式子,然后按分式乘除法法则计算;(2)如果分式的分子、分母是多项式,一般要先将其因式分解,再运算.
乘除混合运算 先将除法统一成乘法,再按从左至右的顺序计算,若有括号要先算括号里面的.
乘方、乘除混合运算 先乘方、再乘除,含有多项式时,通常应先分解因式,能约分的要先约分,再计算.
分式化简求值的方法 (1)先把所给式子化简成最简分式或整式的形式,再将字母的值代入化简后的式子;(2)若题目中给出自主取数值代入求值时,要注意所选取的数值一定要使原分式有意义,即所取数值要使所给式子的分母及除数________0.
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
自主学习
合作探究
自主学习
合作探究
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
