冀教版(新)九上-23.1平均数与加权平均数 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-23.1平均数与加权平均数 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:39 | ||
图片预览










文档简介
(共36张PPT)
23.1平均数与加权平均数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
据资料记载,位于意大利的比萨斜塔1918—1958这41年间,平均每年倾斜1.10毫米;1959—1969这11年间,平均每年倾斜1.26毫米,那么191—1969这52年间,你知道比萨斜塔平均每年倾斜约多少毫米吗?(精确到0.01毫米).
新课精讲
探索新知
1
知识点
算术平均数的计算
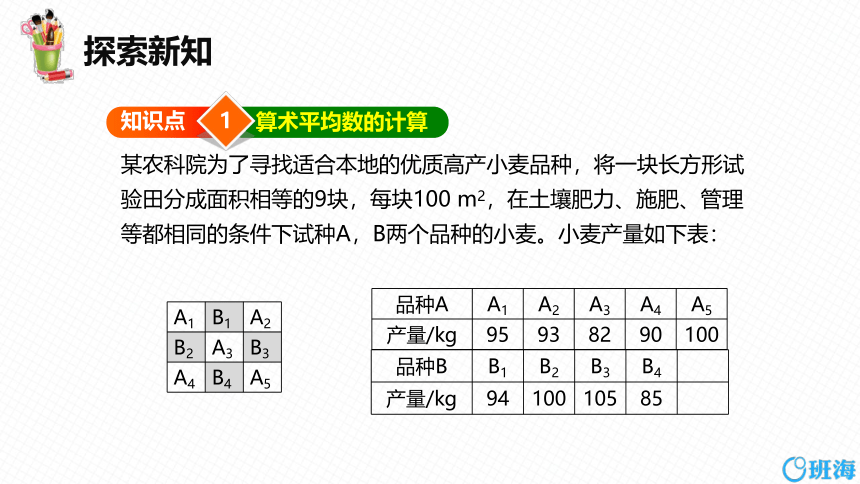
某农科院为了寻找适合本地的优质高产小麦品种,将一块长方形试验田分成面积相等的9块,每块100 m2,在土壤肥力、施肥、管理等都相同的条件下试种A,B两个品种的小麦。小麦产量如下表:
A1 B1 A2
B2 A3 B3
A4 B4 A5
品种A A1 A2 A3 A4 A5
产量/kg 95 93 82 90 100
品种B B1 B2 B3 B4
产量/kg 94 100 105 85
探索新知
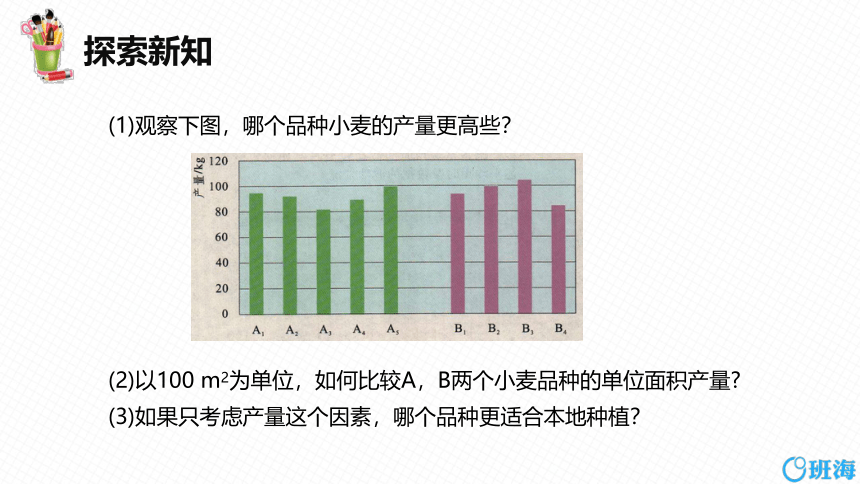
(1)观察下图,哪个品种小麦的产量更高些?
(2)以100 m2为单位,如何比较A,B两个小麦品种的单位面积产量
(3)如果只考虑产量这个因素,哪个品种更适合本地种植?
探索新知
由于同一品种在不同试验田上的产量有差异,要比较两个品种哪个产量高,通常情况下是比较它们的平均产量.
A品种小麦的平均产量:
×(95+93+82+ 90+ 100)=92(kg),
B品种小麦的平均产量:
×(94+100+105+85)=96(kg).
就试验结果来看,B品种小麦比A品种小麦的平均产量高,B品种更适合本地种植.
探索新知
归 纳
一般地,我们把n个数x1,x2,…,xn,的和与n 的比,叫做这n个数的算术平均数 (arithmetic mean),简称平均数,记作 ,读作“x 拔”,即
由于 所以取平均数可以抵消各数据之间的差异. 因此,平均数是一组数据的代表值,它反映了数据的“一般水平”.
探索新知
某次舞蹈大赛的记分规则为:从七位评委的打分中去掉一个最高分和一个最低分后计算平均分作为最后得分.下表是该次比赛中七位评委对小菲与小岚的打分(单位:分):
请通过计算说明谁的最后得分高.
例1
小菲 80 77 82 83 75 78 89
小岚 79 80 77 76 82 85 81
导引:
此题只需按照题中所给“记分规则”将两人的最后得分计算出来,再进行大小比较即可.
探索新知
小菲去掉一个最高分89分,去掉一个最低分75分,
最后得分为
小岚去掉一个最高分85分,去掉一个最低分76分,
最后得分为
因为80分>79.8分,所以小菲的最后得分高.
解:
探索新知
总 结
当数据信息以图表形式呈现时,要结合条件读懂图表,并从中获取有用的信息,本题去掉一个最高分和一个最低分后,数据的个数也发生了变化,计算平均得分时不要忘记这一点.求平均数要牢记是数据总和除以数据总个数.
探索新知
2
知识点
用计算器求平均数
做一做
从一批鸭蛋中任意取出20个,分别称得质量如下:
80 85 70 75 85 85 80 80 75 85
85 80 75 85 80 75 85 70 80 75
(1)整理数据,填写统计表.
(2)求这20个鸭蛋的平均质量.
质量/g 70 75 80 85
频数
探索新知
小明和小亮分别是这样计算平均数的.
小明的计算结果:
×(70+75+80+85)=77.5(g),
小亮的计算结果:
×(70×2+75×5+80×6+85×7)=79.5(g).
你认为他们谁的计算方法正确?请和同学交流你的看法.
探索新知
实际上,小亮的计算方法是正确的. 由于70,75, 80,85出现的频数不同,它们对平均数的影响也不同,所以,频数对平均数起着权衡轻重的作用.
利用计算器可以很方便地计算平均数.以A型计算器为例,求“做一做”中20个数据的平均数的步骤如下:
步 骤 按 键 显 示
选择统计模式,进入一元统计状态
MODE
2
Stat x 0
探索新知
步 骤 按 键 显 示
输入第1个数据70,频数2
输入第2个数据75,频数5
输入第3个数据80,频数6
输入第4个数据85,频数7
显示统计结果
DATA
7
n= 2
0
,
2
DATA
7
n= 7
5
,
5
DATA
8
n= 13
0
,
6
DATA
8
n= 20
5
,
7
Rcl
探索新知
3
知识点
算术平均数的应用
1. 一组数据的平均数是唯一的,它不一定是数据中的某个数据;
2. 平均数是反映数据集中趋势的一个统计量,是反映数据的平均水平(或中等水平)的一个特征量;
3. 一般情况下,平均数能体现一组数据的整体性质.
探索新知
个体户李某经营一家餐馆,下面是在餐馆工作的所有人员去年七月份的工资:
李某6000元,厨师甲900元,厨师乙800元,杂工640元,
招待甲700元,招待乙640元,会计820元.
(1)计算所有人员的平均工资;
(2)平均工资能否反映帮工人员在该月收入的一般水平?
(3)去掉李某后其余人员的平均工资为多少?
(4)平均工资能代表帮工人员该月收入的一般水平吗?
例2
探索新知
(1)根据已知得出总钱数除以7即可得出平均工资;
(2)根据大部分人无法达到1500元,分析即可;
(3)去掉李某工资求出总数除以6即可得出答案;
(4)根据所求数据分析即可.
(1)计算所有人员的平均工资;
分析:
所有人员的平均工资为:
(6000+800+900+640+700+640+820)÷7
=1500(元);
解:
探索新知
(2)平均工资能否反映帮工人员在该月收入的一般水平?
1500元不能反映帮工人员该月收入的一般水平,应为即使工资最高的厨师甲的收入900元,也远小于这个平均数;
(3)去掉李某后其余人员的平均工资为多少?
去掉李某后其余人员的平均工资为:
(800+900+640+700+640+820)÷6=750(元);
(4)后一平均工资能代表帮工人员该月收入的一般水平吗?
750元能代表.
探索新知
总 结
此题主要考查了算术平均数,根据题意正确把握平均数的求法是解题关键.
典题精讲
1.某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,
则他们成绩的平均数是_______.
2.一组数据7,8,10,12,13的平均数是( )
A.7 B.9 C.10 D.12
3.一组数据的和为87,平均数是3,则这组数据的个数为( )
A.87 B.3 C.29 D.90
101
C
C
典题精讲
4.用举手示意的方法调查班上全体同学的年龄,将结果填在下面的表格内,并用计算器计算平均年龄.
5.利用计算器求一组数据的平均数时,一般步骤可分为三步:
①选择统计模式,进入________状态;
②依次输入各________;
③显示________结果.
年龄/岁 14 15 16 合计
人数/名
答案略。
答案略。
典题精讲
6.用计算器计算数据
13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15 B.14.16 C.14.17 D.14.20
B
7.在一次男排比赛中,某队场上6名队员的身高(单位:cm)如下:
193 182 187 174 185 189
(1)求这6名队员的平均身高.
(2)计算每名队员的身高与平均身高的差.这些差的和是多少?
185
答案略。
典题精讲
9.为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是________mg/L.
8.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是________.
8
1
学以致用
小试牛刀
1.一组数据7,8,10,12,13的平均数是( )
A.7 B.9 C.10 D.12
C
2.已知一个班级有40人,数学老师第一次统计这个班的平均成绩为85分,在复查时发现漏记了一个学生的成绩80分,那么这个班的实际平均成绩应为( )
A.85分 B.84.875分 C.87分 D.84.5分
C
小试牛刀
3.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15 B. 14.16 C.14.17 D.14.20
B
4.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输人为15,那么由此求出的平均数与实际平均数的差是( )
A.-3.5 B. 3 C.0.5 D.-3
D
小试牛刀
5.为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到氨氮含量_________mg/L.
1
小试牛刀
6.张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:
①把油箱加满油;②记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:
则在这段时间内,该车每100Km的平均耗油量为( )
A.3L B. 5L C.7.5L D.9L
C
小试牛刀
7.已知某组10名学生的平均成绩为x分,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
B
A. 分 B. 分 C. 分 D. 分
小试牛刀
8.我校举行文艺演出,由参加演出的10个班各派一名同学担任评委,每个节目演出后的得分取各个评委所给分的平均数,下面是各评委给一七年级(3)班一个节目的分数:
(1)该节目的得分是多少分?此得分能否反映该节目的水平?
(2)你对5号和9号评委的给分有什么看法?
(3)你认为怎样计算该节目的分数比较合理?为什么?
小试牛刀
解:(1)该节目的得分 (7.20+7.25+…+7.15)=7.35(分),此得分不能反映该节目的水平.
(2)5号评委给分偏高,9号评委给分偏低,不能公正地代表节目的实际水平.(说法不唯一,意思正确即可)
(3)去掉一个最高分和一个最低分,这样可以避免某些特殊数据带来的负面影响,保证评判的公正性.(说法不唯一,意思正确即可)
课堂小结
课堂小结
(1)本节课你学习了哪些知识
(2)在日常生活中你接触到哪些与平均数有关的事情,说出来和大家交流一下.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
23.1平均数与加权平均数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
据资料记载,位于意大利的比萨斜塔1918—1958这41年间,平均每年倾斜1.10毫米;1959—1969这11年间,平均每年倾斜1.26毫米,那么191—1969这52年间,你知道比萨斜塔平均每年倾斜约多少毫米吗?(精确到0.01毫米).
新课精讲
探索新知
1
知识点
算术平均数的计算
某农科院为了寻找适合本地的优质高产小麦品种,将一块长方形试验田分成面积相等的9块,每块100 m2,在土壤肥力、施肥、管理等都相同的条件下试种A,B两个品种的小麦。小麦产量如下表:
A1 B1 A2
B2 A3 B3
A4 B4 A5
品种A A1 A2 A3 A4 A5
产量/kg 95 93 82 90 100
品种B B1 B2 B3 B4
产量/kg 94 100 105 85
探索新知
(1)观察下图,哪个品种小麦的产量更高些?
(2)以100 m2为单位,如何比较A,B两个小麦品种的单位面积产量
(3)如果只考虑产量这个因素,哪个品种更适合本地种植?
探索新知
由于同一品种在不同试验田上的产量有差异,要比较两个品种哪个产量高,通常情况下是比较它们的平均产量.
A品种小麦的平均产量:
×(95+93+82+ 90+ 100)=92(kg),
B品种小麦的平均产量:
×(94+100+105+85)=96(kg).
就试验结果来看,B品种小麦比A品种小麦的平均产量高,B品种更适合本地种植.
探索新知
归 纳
一般地,我们把n个数x1,x2,…,xn,的和与n 的比,叫做这n个数的算术平均数 (arithmetic mean),简称平均数,记作 ,读作“x 拔”,即
由于 所以取平均数可以抵消各数据之间的差异. 因此,平均数是一组数据的代表值,它反映了数据的“一般水平”.
探索新知
某次舞蹈大赛的记分规则为:从七位评委的打分中去掉一个最高分和一个最低分后计算平均分作为最后得分.下表是该次比赛中七位评委对小菲与小岚的打分(单位:分):
请通过计算说明谁的最后得分高.
例1
小菲 80 77 82 83 75 78 89
小岚 79 80 77 76 82 85 81
导引:
此题只需按照题中所给“记分规则”将两人的最后得分计算出来,再进行大小比较即可.
探索新知
小菲去掉一个最高分89分,去掉一个最低分75分,
最后得分为
小岚去掉一个最高分85分,去掉一个最低分76分,
最后得分为
因为80分>79.8分,所以小菲的最后得分高.
解:
探索新知
总 结
当数据信息以图表形式呈现时,要结合条件读懂图表,并从中获取有用的信息,本题去掉一个最高分和一个最低分后,数据的个数也发生了变化,计算平均得分时不要忘记这一点.求平均数要牢记是数据总和除以数据总个数.
探索新知
2
知识点
用计算器求平均数
做一做
从一批鸭蛋中任意取出20个,分别称得质量如下:
80 85 70 75 85 85 80 80 75 85
85 80 75 85 80 75 85 70 80 75
(1)整理数据,填写统计表.
(2)求这20个鸭蛋的平均质量.
质量/g 70 75 80 85
频数
探索新知
小明和小亮分别是这样计算平均数的.
小明的计算结果:
×(70+75+80+85)=77.5(g),
小亮的计算结果:
×(70×2+75×5+80×6+85×7)=79.5(g).
你认为他们谁的计算方法正确?请和同学交流你的看法.
探索新知
实际上,小亮的计算方法是正确的. 由于70,75, 80,85出现的频数不同,它们对平均数的影响也不同,所以,频数对平均数起着权衡轻重的作用.
利用计算器可以很方便地计算平均数.以A型计算器为例,求“做一做”中20个数据的平均数的步骤如下:
步 骤 按 键 显 示
选择统计模式,进入一元统计状态
MODE
2
Stat x 0
探索新知
步 骤 按 键 显 示
输入第1个数据70,频数2
输入第2个数据75,频数5
输入第3个数据80,频数6
输入第4个数据85,频数7
显示统计结果
DATA
7
n= 2
0
,
2
DATA
7
n= 7
5
,
5
DATA
8
n= 13
0
,
6
DATA
8
n= 20
5
,
7
Rcl
探索新知
3
知识点
算术平均数的应用
1. 一组数据的平均数是唯一的,它不一定是数据中的某个数据;
2. 平均数是反映数据集中趋势的一个统计量,是反映数据的平均水平(或中等水平)的一个特征量;
3. 一般情况下,平均数能体现一组数据的整体性质.
探索新知
个体户李某经营一家餐馆,下面是在餐馆工作的所有人员去年七月份的工资:
李某6000元,厨师甲900元,厨师乙800元,杂工640元,
招待甲700元,招待乙640元,会计820元.
(1)计算所有人员的平均工资;
(2)平均工资能否反映帮工人员在该月收入的一般水平?
(3)去掉李某后其余人员的平均工资为多少?
(4)平均工资能代表帮工人员该月收入的一般水平吗?
例2
探索新知
(1)根据已知得出总钱数除以7即可得出平均工资;
(2)根据大部分人无法达到1500元,分析即可;
(3)去掉李某工资求出总数除以6即可得出答案;
(4)根据所求数据分析即可.
(1)计算所有人员的平均工资;
分析:
所有人员的平均工资为:
(6000+800+900+640+700+640+820)÷7
=1500(元);
解:
探索新知
(2)平均工资能否反映帮工人员在该月收入的一般水平?
1500元不能反映帮工人员该月收入的一般水平,应为即使工资最高的厨师甲的收入900元,也远小于这个平均数;
(3)去掉李某后其余人员的平均工资为多少?
去掉李某后其余人员的平均工资为:
(800+900+640+700+640+820)÷6=750(元);
(4)后一平均工资能代表帮工人员该月收入的一般水平吗?
750元能代表.
探索新知
总 结
此题主要考查了算术平均数,根据题意正确把握平均数的求法是解题关键.
典题精讲
1.某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,
则他们成绩的平均数是_______.
2.一组数据7,8,10,12,13的平均数是( )
A.7 B.9 C.10 D.12
3.一组数据的和为87,平均数是3,则这组数据的个数为( )
A.87 B.3 C.29 D.90
101
C
C
典题精讲
4.用举手示意的方法调查班上全体同学的年龄,将结果填在下面的表格内,并用计算器计算平均年龄.
5.利用计算器求一组数据的平均数时,一般步骤可分为三步:
①选择统计模式,进入________状态;
②依次输入各________;
③显示________结果.
年龄/岁 14 15 16 合计
人数/名
答案略。
答案略。
典题精讲
6.用计算器计算数据
13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15 B.14.16 C.14.17 D.14.20
B
7.在一次男排比赛中,某队场上6名队员的身高(单位:cm)如下:
193 182 187 174 185 189
(1)求这6名队员的平均身高.
(2)计算每名队员的身高与平均身高的差.这些差的和是多少?
185
答案略。
典题精讲
9.为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是________mg/L.
8.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是________.
8
1
学以致用
小试牛刀
1.一组数据7,8,10,12,13的平均数是( )
A.7 B.9 C.10 D.12
C
2.已知一个班级有40人,数学老师第一次统计这个班的平均成绩为85分,在复查时发现漏记了一个学生的成绩80分,那么这个班的实际平均成绩应为( )
A.85分 B.84.875分 C.87分 D.84.5分
C
小试牛刀
3.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15 B. 14.16 C.14.17 D.14.20
B
4.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输人为15,那么由此求出的平均数与实际平均数的差是( )
A.-3.5 B. 3 C.0.5 D.-3
D
小试牛刀
5.为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到氨氮含量_________mg/L.
1
小试牛刀
6.张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:
①把油箱加满油;②记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:
则在这段时间内,该车每100Km的平均耗油量为( )
A.3L B. 5L C.7.5L D.9L
C
小试牛刀
7.已知某组10名学生的平均成绩为x分,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
B
A. 分 B. 分 C. 分 D. 分
小试牛刀
8.我校举行文艺演出,由参加演出的10个班各派一名同学担任评委,每个节目演出后的得分取各个评委所给分的平均数,下面是各评委给一七年级(3)班一个节目的分数:
(1)该节目的得分是多少分?此得分能否反映该节目的水平?
(2)你对5号和9号评委的给分有什么看法?
(3)你认为怎样计算该节目的分数比较合理?为什么?
小试牛刀
解:(1)该节目的得分 (7.20+7.25+…+7.15)=7.35(分),此得分不能反映该节目的水平.
(2)5号评委给分偏高,9号评委给分偏低,不能公正地代表节目的实际水平.(说法不唯一,意思正确即可)
(3)去掉一个最高分和一个最低分,这样可以避免某些特殊数据带来的负面影响,保证评判的公正性.(说法不唯一,意思正确即可)
课堂小结
课堂小结
(1)本节课你学习了哪些知识
(2)在日常生活中你接触到哪些与平均数有关的事情,说出来和大家交流一下.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
