冀教版(新)九上-23.3 方差 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-23.3 方差 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
23.3 方 差
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验。
新课精讲
探索新知
1
类型
方差与平均数在数据分析中应用
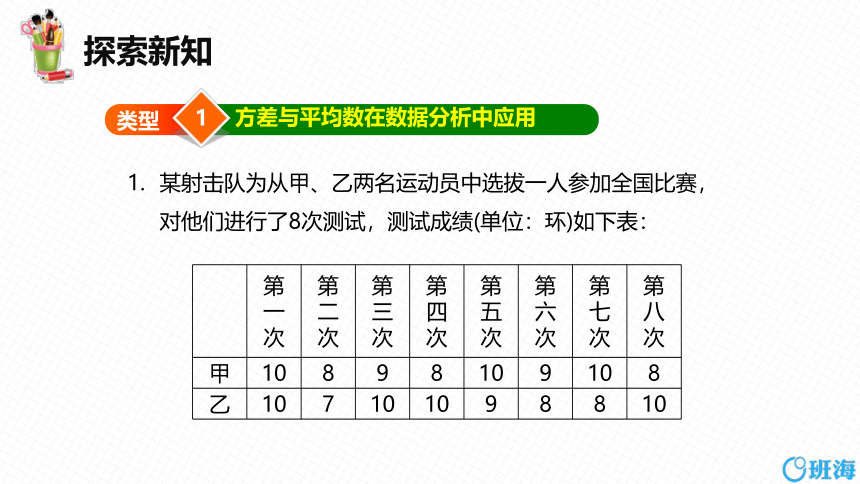
某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第 一 次 第 二 次 第 三 次 第 四 次 第 五 次 第 六 次 第 七 次 第
八
次
甲 10 8 9 8 10 9 10 8
乙 10 7 10 10 9 8 8 10
探索新知
(1)根据表格中的数据,计算出甲的平均成绩是________环,乙的平均成绩是________环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.
(2)s甲2= [(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10
-9)2+(9-9)2+(10-9)2+(8-9)2]=0.75,
s乙2= [(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9
-9)2+(8-9)2+(8-9)2+(10-9)2]=1.25.
(3)因为甲、乙平均成绩相同,且0.75<1.25,所以甲的方差小,甲比较稳定,故选甲参加全国比赛更合适.
解:
9
9
探索新知
2
方差与中位数在数据分析中应用
类型
2.我校准备挑选一名跳高运动员参加江东区中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
(2)哪名运动员的成绩更为稳定?为什么?
(3)若预测,跳过165 cm就很可能获得冠军.该校为了获得冠军,可能选哪位运动员参赛?若预测跳过170 cm才能得冠军呢?
探索新知
(1)甲的平均成绩为169 cm,乙的平均成绩为168 cm;
(2)s甲2=6,s乙2=31.5,所以甲运动员的成绩更为稳定;
(3)若跳过165 cm就很可能获得冠军,则在8次成绩中,甲8次都跳过了165 cm,而乙只有5次,所以应选甲运动员参加;若跳过170 cm才能得冠军,则在8次成绩中,甲只有3次都跳过了170 cm,而乙有5次,所以应选乙运动员参加.
解:
探索新知
3
方差与统计表的信息在数据分析中应用
类型
3.甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 众数 中位数 方差
甲 8 8 0.4
乙 9 3.2
探索新知
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差________(填“变大”“变小”或“不变”).
(1)填表如下:
解:
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
平均数 众数 中位数 方差
甲 8 8 8 0.4
乙 8 9 9 3.2
变小
探索新知
4
方差与统计图表的信息在数据中应用
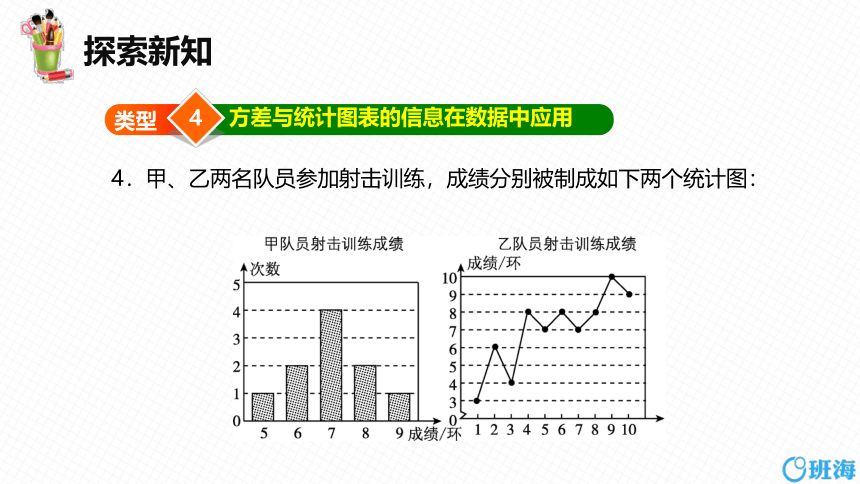
4.甲、乙两名队员参加射击训练,成绩分别被制成如下两个统计图:
类型
探索新知
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1)写出表格中a,b,c 的值.
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
解:(1)a=7,b=7.5,c=4.2.
探索新知
(2)从平均成绩看甲、乙二人的平均成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名队员参赛,可选择乙参赛,因为乙获得较好成绩的可能更大.
典题精讲
1.甲、乙两名队员参加射击训练,成绩分别被制成如下两个统计图:
根据以上信息,整理分析数据如下:
典题精讲
(1)写出表格中a,b,c的值.
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
典题精讲
解:(1)a=7,b=7.5,c=4.2.
(2)从平均成绩看甲、乙二人的平均成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.
综合以上各因素,若选派一名队员参赛,可选择乙参赛,因为乙获得较好成绩的可能更大.
典题精讲
2.为了让广大青少年学生走向操场,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.硕硕和强强在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,测得他们的成绩如图,请根据图中所示解答以下问题.
典题精讲
(1)请根据图中信息,补全下面的表格.
(2)分别计算他们成绩的平均数和方差并填入表格,若你是他们的教练,将硕硕与强强的成绩比较后,你将分别给予他们怎样的建议?
平均数 方差
硕硕
强强
次数 1 2 3 4 5
硕硕 13.3 13.4 13.3 13.3
强强 13.2 13.1 13.5 13.3
典题精讲
解:(1)
次数 1 2 3 4 5
硕硕 13.3 13.4 13.3 13.2 13.3
强强 13.2 13.4 13.1 13.5 13.3
(2)
平均数 方差
硕硕 13.3 0.004
强强 13.3 0.02
学以致用
小试牛刀
1.2018年3月12日植树节当天,九年级某班同学分成10个小组参加植树造林活动,10个小组植树的株数为:5,6,5,6,5,7,7,6,6,7(单位:株).则这10个小组植树株数的方差和众数分别是( )
A.6,5 B.0.6,6 C.6,6 D.0.6,7
B
2.若一个样本是3,-1,a,1,-3,3.它们的平均数是a 的
则这个样本的方差是________.
小试牛刀
3.甲、乙两个同学在四次模拟考试中,数学的平均成绩都是112分,
方差分别是 则成绩比较稳定的是( )
A.甲 B.乙 C.甲和乙一样 D.无法确定
A
4.信和商厦一女装专柜对上周女装的销售情况进行了统计,销售情况如下表所示.经理决定本周多进一些红色的女装,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量/件 100 180 220 80 550
A.方差 B.众数 C.平均数 D.中位数
B
小试牛刀
5.某校九年级(二)班的10名团员在献爱心捐款活动中,捐款情况如下(单位:元):10,8,12,15,10,12,11,9,13,10.则这组数据的( )
A.众数是10.5 B.平均数是10 C.方差是3.8 D.中位数是10
C
6.在方差的计算公式 中,数字10和20分别表示的意义是( )
A.数据的个数和方差 B.平均数和数据的个数
C.数据的个数和平均数 D.数据的方差和平均数
C
小试牛刀
7.甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差______(填“变大”“变小”或“不变”).
小试牛刀
解:(1)
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳,所以选择甲参加射击比赛;
(3)变小。
小试牛刀
8.我校准备挑选一名跳高运动员参加江东区中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
(2)哪名运动员的成绩更为稳定?为什么?
(3)若预测,跳过165cm就很可能获得冠军.该校为了获得冠军,可能选哪位运动员参赛?若预测跳过170cm才能得冠军呢?
小试牛刀
解:(1)甲的平均成绩为169cm,乙的平均成绩为168cm;
(2) 所以甲运动员的成绩更为稳定;
(3)若跳过165cm就很可能获得冠军,则在8次成绩中,甲8次都跳过了165cm,而乙只有5次,所以应选甲运动员参加;若跳过170cm才能得冠军,则在8次成绩中,甲只有3次都跳过了170cm,而乙有5次,所以应选乙运动员参加.
课堂小结
课堂小结
数据分析的方法:
(1)理解平均数、中位数、众数反映的是数据的集中趋势,方差与标准差反映的是数据的波动程度.
(2)在具体问题中,根据实际问题灵活选择合适的数据解决相关问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
23.3 方 差
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验。
新课精讲
探索新知
1
类型
方差与平均数在数据分析中应用
某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第 一 次 第 二 次 第 三 次 第 四 次 第 五 次 第 六 次 第 七 次 第
八
次
甲 10 8 9 8 10 9 10 8
乙 10 7 10 10 9 8 8 10
探索新知
(1)根据表格中的数据,计算出甲的平均成绩是________环,乙的平均成绩是________环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.
(2)s甲2= [(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10
-9)2+(9-9)2+(10-9)2+(8-9)2]=0.75,
s乙2= [(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9
-9)2+(8-9)2+(8-9)2+(10-9)2]=1.25.
(3)因为甲、乙平均成绩相同,且0.75<1.25,所以甲的方差小,甲比较稳定,故选甲参加全国比赛更合适.
解:
9
9
探索新知
2
方差与中位数在数据分析中应用
类型
2.我校准备挑选一名跳高运动员参加江东区中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
(2)哪名运动员的成绩更为稳定?为什么?
(3)若预测,跳过165 cm就很可能获得冠军.该校为了获得冠军,可能选哪位运动员参赛?若预测跳过170 cm才能得冠军呢?
探索新知
(1)甲的平均成绩为169 cm,乙的平均成绩为168 cm;
(2)s甲2=6,s乙2=31.5,所以甲运动员的成绩更为稳定;
(3)若跳过165 cm就很可能获得冠军,则在8次成绩中,甲8次都跳过了165 cm,而乙只有5次,所以应选甲运动员参加;若跳过170 cm才能得冠军,则在8次成绩中,甲只有3次都跳过了170 cm,而乙有5次,所以应选乙运动员参加.
解:
探索新知
3
方差与统计表的信息在数据分析中应用
类型
3.甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 众数 中位数 方差
甲 8 8 0.4
乙 9 3.2
探索新知
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差________(填“变大”“变小”或“不变”).
(1)填表如下:
解:
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
平均数 众数 中位数 方差
甲 8 8 8 0.4
乙 8 9 9 3.2
变小
探索新知
4
方差与统计图表的信息在数据中应用
4.甲、乙两名队员参加射击训练,成绩分别被制成如下两个统计图:
类型
探索新知
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1)写出表格中a,b,c 的值.
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
解:(1)a=7,b=7.5,c=4.2.
探索新知
(2)从平均成绩看甲、乙二人的平均成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名队员参赛,可选择乙参赛,因为乙获得较好成绩的可能更大.
典题精讲
1.甲、乙两名队员参加射击训练,成绩分别被制成如下两个统计图:
根据以上信息,整理分析数据如下:
典题精讲
(1)写出表格中a,b,c的值.
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
典题精讲
解:(1)a=7,b=7.5,c=4.2.
(2)从平均成绩看甲、乙二人的平均成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.
综合以上各因素,若选派一名队员参赛,可选择乙参赛,因为乙获得较好成绩的可能更大.
典题精讲
2.为了让广大青少年学生走向操场,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.硕硕和强强在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,测得他们的成绩如图,请根据图中所示解答以下问题.
典题精讲
(1)请根据图中信息,补全下面的表格.
(2)分别计算他们成绩的平均数和方差并填入表格,若你是他们的教练,将硕硕与强强的成绩比较后,你将分别给予他们怎样的建议?
平均数 方差
硕硕
强强
次数 1 2 3 4 5
硕硕 13.3 13.4 13.3 13.3
强强 13.2 13.1 13.5 13.3
典题精讲
解:(1)
次数 1 2 3 4 5
硕硕 13.3 13.4 13.3 13.2 13.3
强强 13.2 13.4 13.1 13.5 13.3
(2)
平均数 方差
硕硕 13.3 0.004
强强 13.3 0.02
学以致用
小试牛刀
1.2018年3月12日植树节当天,九年级某班同学分成10个小组参加植树造林活动,10个小组植树的株数为:5,6,5,6,5,7,7,6,6,7(单位:株).则这10个小组植树株数的方差和众数分别是( )
A.6,5 B.0.6,6 C.6,6 D.0.6,7
B
2.若一个样本是3,-1,a,1,-3,3.它们的平均数是a 的
则这个样本的方差是________.
小试牛刀
3.甲、乙两个同学在四次模拟考试中,数学的平均成绩都是112分,
方差分别是 则成绩比较稳定的是( )
A.甲 B.乙 C.甲和乙一样 D.无法确定
A
4.信和商厦一女装专柜对上周女装的销售情况进行了统计,销售情况如下表所示.经理决定本周多进一些红色的女装,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量/件 100 180 220 80 550
A.方差 B.众数 C.平均数 D.中位数
B
小试牛刀
5.某校九年级(二)班的10名团员在献爱心捐款活动中,捐款情况如下(单位:元):10,8,12,15,10,12,11,9,13,10.则这组数据的( )
A.众数是10.5 B.平均数是10 C.方差是3.8 D.中位数是10
C
6.在方差的计算公式 中,数字10和20分别表示的意义是( )
A.数据的个数和方差 B.平均数和数据的个数
C.数据的个数和平均数 D.数据的方差和平均数
C
小试牛刀
7.甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差______(填“变大”“变小”或“不变”).
小试牛刀
解:(1)
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳,所以选择甲参加射击比赛;
(3)变小。
小试牛刀
8.我校准备挑选一名跳高运动员参加江东区中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
(2)哪名运动员的成绩更为稳定?为什么?
(3)若预测,跳过165cm就很可能获得冠军.该校为了获得冠军,可能选哪位运动员参赛?若预测跳过170cm才能得冠军呢?
小试牛刀
解:(1)甲的平均成绩为169cm,乙的平均成绩为168cm;
(2) 所以甲运动员的成绩更为稳定;
(3)若跳过165cm就很可能获得冠军,则在8次成绩中,甲8次都跳过了165cm,而乙只有5次,所以应选甲运动员参加;若跳过170cm才能得冠军,则在8次成绩中,甲只有3次都跳过了170cm,而乙有5次,所以应选乙运动员参加.
课堂小结
课堂小结
数据分析的方法:
(1)理解平均数、中位数、众数反映的是数据的集中趋势,方差与标准差反映的是数据的波动程度.
(2)在具体问题中,根据实际问题灵活选择合适的数据解决相关问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
