冀教版(新)九上-23.4 用样本估计总体【优质课件】
文档属性
| 名称 | 冀教版(新)九上-23.4 用样本估计总体【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共40张PPT)
23.4 用样本估计总体
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在“数据的收集与整理”一章中,我们已经学习了如何用样本数据信息估计总体的分布. 在本节课,我们来了解用样本平均数(或方差) 估计总体平均数(或方差)的统计方法.
新课精讲
探索新知
1
知识点
用样本平均数估计总体平均数
为了估计全校初中女生的平均身高,九年级(1)班8个课外学习小组采用随机抽样的方法,分别抽取容量为25和100的样本,样本平均数用 表示,结果(单位:cm)如下表:
小组序号 1 2 3 4 5 6 7 8
158.5 161.5 160.2 160.0 160.9 160.4 159.0 159.5
160.0 159.0 160.5 159.3 159.8 161.0 159.6 160.8
探索新知
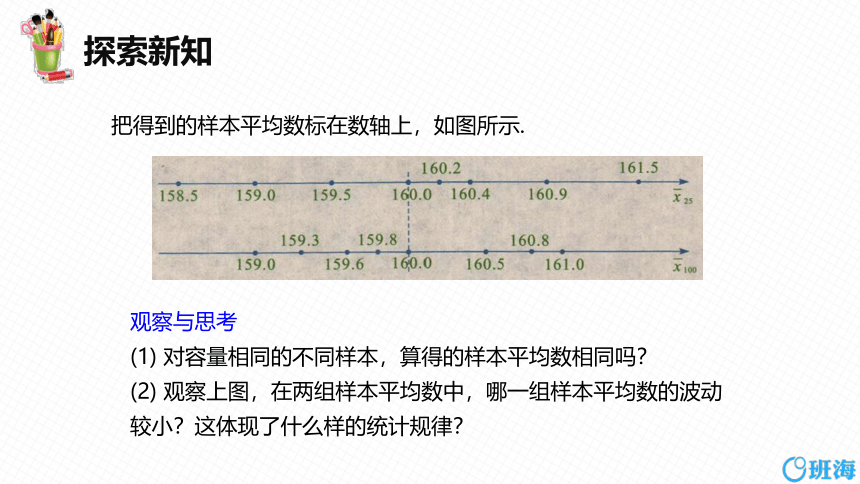
把得到的样本平均数标在数轴上,如图所示.
观察与思考
(1) 对容量相同的不同样本,算得的样本平均数相同吗?
(2) 观察上图,在两组样本平均数中,哪一组样本平均数的波动
较小?这体现了什么样的统计规律?
探索新知
(3) 如果总体身高的平均数为160. 0 cm,哪一组样本平均数整体上
更接近 160. 0 cm
由于抽样的任意性,即使是相同的样本容量,不同样本的平均数一般也不相同;当样本容量较小时,差异可能还较大.但是当样本容量增大时,样本的平均数的波动变小,逐渐趋于稳定,且与总体的平均数比较接近.因此,在实际中经常用样本的平均数估计总体的平均数.同样的道理,我们也用样本的方差估计总体的方差.
探索新知
当所要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.例如,实际生活中经常用样本的平均数来估计总体的平均数.
要点精析:
(1)用样本估计总体时,样本容量越大,样本对总体的估计越准确,相应的工作量及破坏性也越大,因此样本容量的确定,既要考虑问题本身的需要,又要考虑实现的可能性及付出的代价.
(2)抽取的样本要具有一般性和代表性.
探索新知
工人师傅用车床加工一种直径为20 mm的轴,从某天加工的轴中随机抽取了10件,测得其直径(单位:mm)如下:
20. 1 19. 9 20. 3 20. 2 19. 8 19. 7 19. 9
20. 3 20. 0 19. 8
(1)计算样本平均数和样本方差.
(2)求总体平均数和总体方差的估计值.
(3)规定当方差不超过0.05 mm2时,车床生产情况为正常.判断
这台车床的生产情况是否正常.
例1
探索新知
(1)样本平均数为
样本方差为
(2)总体平均数和总体方差的估计值分别为20 mm和0. 042 mm2.
(3)由于方差不超过0.05 mm2,所以可以认为车床的生产情况正常.
解:
探索新知
2
知识点
用样本方差估计总体方差
探究
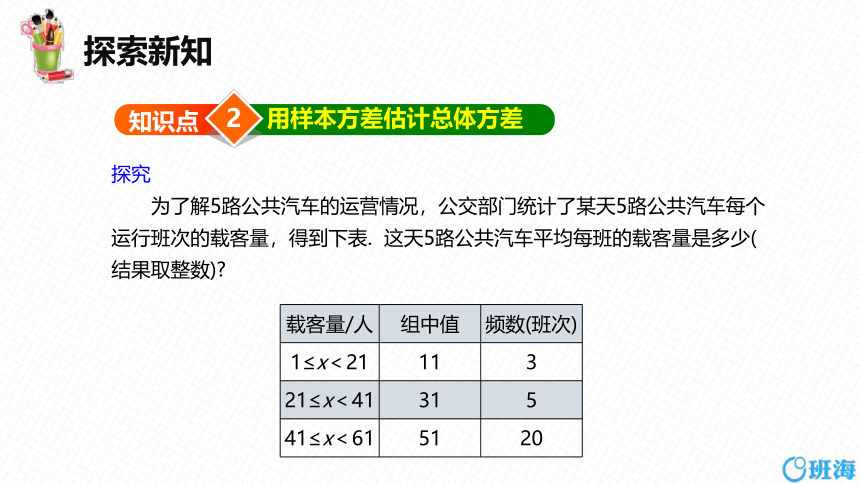
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表. 这天5路公共汽车平均每班的载客量是多少(结果取整数)
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
探索新知
载客量/人 组中值 频数(班次)
61≤x<81 71 22
81≤x<101 91 18
101≤x<121 111 15
注:数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数. 例如,小组1≤x<21的组中值为
探索新知
根据上面的频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权. 例如在1≤x<21之间的载客量近似地看作组中值11,组中值11的权是它的频数3. 因此这天5路公共汽车平均每班的载客量是
探索新知
归 纳
当所给的数据是一个范围时,不是准确数值时,通常取中间值来解答.
1. 用样本的方差去估计总体的方差也是重要的统计思想.
2.易错警示:
由于抽样的任意性,不同的样本的方差一般也不同.当样本数据较少时,差异可能还很大.但是,当样本中的数据较多,且具有较好的代表性时,样本的方差趋于稳定,且与总体的方差比较接近.因此,我们经常用样本的方差估计总体的方差,分析数据后科学决策.
探索新知
一个苹果园,共有2 000棵树龄相同的苹果树. 为了估计今年苹果的总产量,任意选择了6 棵苹果树,数出它们挂果的数量(单位:个)分别为:
260 340 280 420 360 380
根据往年的经验,平均每个苹果的质量约为250 g.
试估计今年苹果 园苹果的总产量.
例2
探索新知
6棵苹果树平均挂果的数量为
×(260+340+280+420+360+380)=340(个)
0.25×340=85(kg),
6棵苹果树平均每棵的产量约为85 kg.
由样本平均数估计总体平均数,2 000棵苹果树平均每棵产量约为85 kg,总产量的估计值为85×2 000 =170 000(kg).
解:
探索新知
总 结
用样本的平均数、方差估计总体的平均数、方差是抽样调查的重要目的之一.注意样本容量要足够大.
典题精讲
1.某单位有1名经理、2名主任、2名助理和11名普通职员,他们的月工资
各不相同.若该单位员工的月平均工资是1 500元,则下列说法中正确的
是( )
A.所有员工的月工资都是1 500元
B.一定有一名员工的月工资是1 500元
C.至少有一名员工的月工资高于1 500元
D.一定有一半员工的月工资高于1 500元
C
典题精讲
2. 黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%,
请估计黄石地区1 000斤蚕豆种子中不能发芽的大约有( )
A.971斤 B.129斤
C.97.1斤 D.29斤
D
3.从总体中抽取一个样本,计算出样本方差为2,可以估计总体方差( )
A.一定大于2
B.约等于2
C.一定等于2
D.与样本方差无关
B
典题精讲
4.从总体中抽取一部分数据作为样本去估计总体的某种属性.下面叙述正确的是( )
A.样本容量越大,样本平均数就越大
B.样本容量越大,样本的方差就越大
C.样本容量越大,样本的中位数就越大
D.样本容量越大,对总体的估计就越准确
D
典题精讲
5.为了估计一批鸡蛋中每个鸡蛋的平均质量p (单位:g),小红专挑个儿大
的鸡蛋30个,称得总质量为1.8 kg.小明随意拿出40个鸡蛋,称得总质量为
2.2kg.
(1)分别计算小红、小明选出的鸡蛋的平均质量.
(2)用样本平均数估计p,小红和小明谁的结果更客观些?
解:(1)
解:(2)
典题精讲
6.某养鱼户经营池塘养鱼.放养鱼苗20 000尾,其成活率约为70%.
在秋季捕捞时,随意捞出10尾鱼,称得每尾的质量(单位:kg)如下:
0.8 0.9 1.2 1.3 0.8 1.1 1.0 1.2 0.8 0.9
(1)根据样本平均数估计这塘鱼的总质量是多少千克?
(2)如果把这塘鱼全部卖掉,其市场售价每千克4元,那么能收入多少元?除去当年的投资成本16000元,第一年纯收入多少元?
(3)已知该养鱼户这三年纯收入为132400元,求第二年、第三年平均每年的增长率是多少?
典题精讲
(1)(0.8+0.9+1.2+1.3+0.8+1.1+1.0+1.2+0.8+0.9)÷10=1.0(kg).
总产量:1.0×20000×70%=14000(kg).
故这塘鱼的总产量约是14000千克;
(2)第一年收入:14000×4=56000(元),
第一年纯收入:56000-16000=40000(元).故第一年纯收入40000元;
(3)设每年平均增长率为x,由题意,得
40000+40000(1+x)+40000(1+x)2=132400,
得x1=0.1,x2=-3.1(不合题意舍去).
故第二年、第三年平均每年的增长率是10%.
学以致用
小试牛刀
1. 积极行动起来,共建节约型社会!我市某居民小区200户居民参加了节水行动,现统计了10户家庭一个月的节水情况,将有关数据整理如下:
请你估计该200户家庭这个月节约用水的总量是( )
A.240吨 B.360吨 C.180吨 D.200吨
A
2.样本方差的大小,可以反映( )
A.样本的平均水平 B.总体的平均水平
C.众数的情况 D.总体的波动大小
B
小试牛刀
3.某学校为鼓励学生课外阅读,制定了“阅读奖励方案”. 方案公布后,随机征求了100名学生的意见,并对持“赞成”“反对”“弃权”
三种意见的人数进行统计,绘制成如图所示的扇形统计图.若该校有2000名学生,则赞成该方案的学生大约有_________人.
1400
小试牛刀
4.市运会举行射击比赛,校射击队从甲、乙、丙、丁四人中选拔一人参赛.在选拔赛中,每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.
请你根据表中数据选一人参加比赛,最合适的人选是_________.
丁
小试牛刀
5.如图所示的是小强同学根据沧州城区某天上午和下午各四个整时点的气温绘制成的折线统计图,该天上午和下午气温比较稳定的是( )
B
A.上午 B.下午 C.上午与下午稳定情况相同 D.无法确定
小试牛刀
6.为保护环境,创建绿色鹰潭,某环保小组随机调查了某市区30个家庭一天丢弃塑料袋的情况,统计结果如下表:
(1)这种调查方式属于普查还是抽样调查?
(2)这30个家庭一天丢弃塑料袋个数的众数是_____个,中位数是 _____ 个.
(3)该市区人口约44万,假设平均一个家庭有4个人.若根据30个家庭这一天丢弃塑料袋个数的平均数估算,则全市一天丢弃塑料袋的总数约是多少个.通过该环保小组的统计和你的估算,你有何感想或对市民提一条科学的建议!
小试牛刀
解:(1)抽样调查.
(2)2,3.
(3)因为样本 因为全市一天丢弃塑料袋的总数为
.
感想:生活垃圾不统不知道,一统吓一跳等.
建议:少用一次性塑料袋,多用健康环保袋;爱护环境,从我做起或人人有责等.
小试牛刀
7.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图所示的两幅不完整的统计图.
根据以上信息解答下列问题:
(1)回收的问卷数为120份,“严加干涉”部分对应扇形的圆心角度数为300;
(2)把条形统计图补充完整;
小试牛刀
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人.
小试牛刀
解:(1)120,30°.
(2)
(3)
小试牛刀
8.经市场调查,某种优质西瓜质量为(5土0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A,B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
A.4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B.4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9 5.4
5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.3
小试牛刀
(1)若质量为(5士0.25)kg的为优等品,根据以上信息完成下表:
(2)请分别从优等品数量、平均数与方差三方面对A,B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
小试牛刀
解:(1)
(2)从优等品数量的角度看,因A技术种植的西瓜优等品数量较多,所以A技术较好;从平均数的角度看,因A技术种植的西瓜质量的平均数更接近5kg,所以A技术较好;从方差的角度看,因B技术种植的西瓜质量的方差较小,所以B技术种植的西瓜质量更为稳定.从市场销售角度看,因优等品比较畅销,A技术种植的西瓜优等品数量比较多,且平均质量更接近5kg,因而更适合推广A种技术.
课堂小结
课堂小结
抽样调查体现的样本估计总体的数学思想是统计的基本思想,一般是用样本的某些特征估计总体的某些特征.同一组数据,所选取的样本不同,平均数、方差等统计量结果也不相同.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
23.4 用样本估计总体
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在“数据的收集与整理”一章中,我们已经学习了如何用样本数据信息估计总体的分布. 在本节课,我们来了解用样本平均数(或方差) 估计总体平均数(或方差)的统计方法.
新课精讲
探索新知
1
知识点
用样本平均数估计总体平均数
为了估计全校初中女生的平均身高,九年级(1)班8个课外学习小组采用随机抽样的方法,分别抽取容量为25和100的样本,样本平均数用 表示,结果(单位:cm)如下表:
小组序号 1 2 3 4 5 6 7 8
158.5 161.5 160.2 160.0 160.9 160.4 159.0 159.5
160.0 159.0 160.5 159.3 159.8 161.0 159.6 160.8
探索新知
把得到的样本平均数标在数轴上,如图所示.
观察与思考
(1) 对容量相同的不同样本,算得的样本平均数相同吗?
(2) 观察上图,在两组样本平均数中,哪一组样本平均数的波动
较小?这体现了什么样的统计规律?
探索新知
(3) 如果总体身高的平均数为160. 0 cm,哪一组样本平均数整体上
更接近 160. 0 cm
由于抽样的任意性,即使是相同的样本容量,不同样本的平均数一般也不相同;当样本容量较小时,差异可能还较大.但是当样本容量增大时,样本的平均数的波动变小,逐渐趋于稳定,且与总体的平均数比较接近.因此,在实际中经常用样本的平均数估计总体的平均数.同样的道理,我们也用样本的方差估计总体的方差.
探索新知
当所要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.例如,实际生活中经常用样本的平均数来估计总体的平均数.
要点精析:
(1)用样本估计总体时,样本容量越大,样本对总体的估计越准确,相应的工作量及破坏性也越大,因此样本容量的确定,既要考虑问题本身的需要,又要考虑实现的可能性及付出的代价.
(2)抽取的样本要具有一般性和代表性.
探索新知
工人师傅用车床加工一种直径为20 mm的轴,从某天加工的轴中随机抽取了10件,测得其直径(单位:mm)如下:
20. 1 19. 9 20. 3 20. 2 19. 8 19. 7 19. 9
20. 3 20. 0 19. 8
(1)计算样本平均数和样本方差.
(2)求总体平均数和总体方差的估计值.
(3)规定当方差不超过0.05 mm2时,车床生产情况为正常.判断
这台车床的生产情况是否正常.
例1
探索新知
(1)样本平均数为
样本方差为
(2)总体平均数和总体方差的估计值分别为20 mm和0. 042 mm2.
(3)由于方差不超过0.05 mm2,所以可以认为车床的生产情况正常.
解:
探索新知
2
知识点
用样本方差估计总体方差
探究
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表. 这天5路公共汽车平均每班的载客量是多少(结果取整数)
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
探索新知
载客量/人 组中值 频数(班次)
61≤x<81 71 22
81≤x<101 91 18
101≤x<121 111 15
注:数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数. 例如,小组1≤x<21的组中值为
探索新知
根据上面的频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权. 例如在1≤x<21之间的载客量近似地看作组中值11,组中值11的权是它的频数3. 因此这天5路公共汽车平均每班的载客量是
探索新知
归 纳
当所给的数据是一个范围时,不是准确数值时,通常取中间值来解答.
1. 用样本的方差去估计总体的方差也是重要的统计思想.
2.易错警示:
由于抽样的任意性,不同的样本的方差一般也不同.当样本数据较少时,差异可能还很大.但是,当样本中的数据较多,且具有较好的代表性时,样本的方差趋于稳定,且与总体的方差比较接近.因此,我们经常用样本的方差估计总体的方差,分析数据后科学决策.
探索新知
一个苹果园,共有2 000棵树龄相同的苹果树. 为了估计今年苹果的总产量,任意选择了6 棵苹果树,数出它们挂果的数量(单位:个)分别为:
260 340 280 420 360 380
根据往年的经验,平均每个苹果的质量约为250 g.
试估计今年苹果 园苹果的总产量.
例2
探索新知
6棵苹果树平均挂果的数量为
×(260+340+280+420+360+380)=340(个)
0.25×340=85(kg),
6棵苹果树平均每棵的产量约为85 kg.
由样本平均数估计总体平均数,2 000棵苹果树平均每棵产量约为85 kg,总产量的估计值为85×2 000 =170 000(kg).
解:
探索新知
总 结
用样本的平均数、方差估计总体的平均数、方差是抽样调查的重要目的之一.注意样本容量要足够大.
典题精讲
1.某单位有1名经理、2名主任、2名助理和11名普通职员,他们的月工资
各不相同.若该单位员工的月平均工资是1 500元,则下列说法中正确的
是( )
A.所有员工的月工资都是1 500元
B.一定有一名员工的月工资是1 500元
C.至少有一名员工的月工资高于1 500元
D.一定有一半员工的月工资高于1 500元
C
典题精讲
2. 黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%,
请估计黄石地区1 000斤蚕豆种子中不能发芽的大约有( )
A.971斤 B.129斤
C.97.1斤 D.29斤
D
3.从总体中抽取一个样本,计算出样本方差为2,可以估计总体方差( )
A.一定大于2
B.约等于2
C.一定等于2
D.与样本方差无关
B
典题精讲
4.从总体中抽取一部分数据作为样本去估计总体的某种属性.下面叙述正确的是( )
A.样本容量越大,样本平均数就越大
B.样本容量越大,样本的方差就越大
C.样本容量越大,样本的中位数就越大
D.样本容量越大,对总体的估计就越准确
D
典题精讲
5.为了估计一批鸡蛋中每个鸡蛋的平均质量p (单位:g),小红专挑个儿大
的鸡蛋30个,称得总质量为1.8 kg.小明随意拿出40个鸡蛋,称得总质量为
2.2kg.
(1)分别计算小红、小明选出的鸡蛋的平均质量.
(2)用样本平均数估计p,小红和小明谁的结果更客观些?
解:(1)
解:(2)
典题精讲
6.某养鱼户经营池塘养鱼.放养鱼苗20 000尾,其成活率约为70%.
在秋季捕捞时,随意捞出10尾鱼,称得每尾的质量(单位:kg)如下:
0.8 0.9 1.2 1.3 0.8 1.1 1.0 1.2 0.8 0.9
(1)根据样本平均数估计这塘鱼的总质量是多少千克?
(2)如果把这塘鱼全部卖掉,其市场售价每千克4元,那么能收入多少元?除去当年的投资成本16000元,第一年纯收入多少元?
(3)已知该养鱼户这三年纯收入为132400元,求第二年、第三年平均每年的增长率是多少?
典题精讲
(1)(0.8+0.9+1.2+1.3+0.8+1.1+1.0+1.2+0.8+0.9)÷10=1.0(kg).
总产量:1.0×20000×70%=14000(kg).
故这塘鱼的总产量约是14000千克;
(2)第一年收入:14000×4=56000(元),
第一年纯收入:56000-16000=40000(元).故第一年纯收入40000元;
(3)设每年平均增长率为x,由题意,得
40000+40000(1+x)+40000(1+x)2=132400,
得x1=0.1,x2=-3.1(不合题意舍去).
故第二年、第三年平均每年的增长率是10%.
学以致用
小试牛刀
1. 积极行动起来,共建节约型社会!我市某居民小区200户居民参加了节水行动,现统计了10户家庭一个月的节水情况,将有关数据整理如下:
请你估计该200户家庭这个月节约用水的总量是( )
A.240吨 B.360吨 C.180吨 D.200吨
A
2.样本方差的大小,可以反映( )
A.样本的平均水平 B.总体的平均水平
C.众数的情况 D.总体的波动大小
B
小试牛刀
3.某学校为鼓励学生课外阅读,制定了“阅读奖励方案”. 方案公布后,随机征求了100名学生的意见,并对持“赞成”“反对”“弃权”
三种意见的人数进行统计,绘制成如图所示的扇形统计图.若该校有2000名学生,则赞成该方案的学生大约有_________人.
1400
小试牛刀
4.市运会举行射击比赛,校射击队从甲、乙、丙、丁四人中选拔一人参赛.在选拔赛中,每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.
请你根据表中数据选一人参加比赛,最合适的人选是_________.
丁
小试牛刀
5.如图所示的是小强同学根据沧州城区某天上午和下午各四个整时点的气温绘制成的折线统计图,该天上午和下午气温比较稳定的是( )
B
A.上午 B.下午 C.上午与下午稳定情况相同 D.无法确定
小试牛刀
6.为保护环境,创建绿色鹰潭,某环保小组随机调查了某市区30个家庭一天丢弃塑料袋的情况,统计结果如下表:
(1)这种调查方式属于普查还是抽样调查?
(2)这30个家庭一天丢弃塑料袋个数的众数是_____个,中位数是 _____ 个.
(3)该市区人口约44万,假设平均一个家庭有4个人.若根据30个家庭这一天丢弃塑料袋个数的平均数估算,则全市一天丢弃塑料袋的总数约是多少个.通过该环保小组的统计和你的估算,你有何感想或对市民提一条科学的建议!
小试牛刀
解:(1)抽样调查.
(2)2,3.
(3)因为样本 因为全市一天丢弃塑料袋的总数为
.
感想:生活垃圾不统不知道,一统吓一跳等.
建议:少用一次性塑料袋,多用健康环保袋;爱护环境,从我做起或人人有责等.
小试牛刀
7.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图所示的两幅不完整的统计图.
根据以上信息解答下列问题:
(1)回收的问卷数为120份,“严加干涉”部分对应扇形的圆心角度数为300;
(2)把条形统计图补充完整;
小试牛刀
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人.
小试牛刀
解:(1)120,30°.
(2)
(3)
小试牛刀
8.经市场调查,某种优质西瓜质量为(5土0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A,B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
A.4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B.4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9 5.4
5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.3
小试牛刀
(1)若质量为(5士0.25)kg的为优等品,根据以上信息完成下表:
(2)请分别从优等品数量、平均数与方差三方面对A,B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
小试牛刀
解:(1)
(2)从优等品数量的角度看,因A技术种植的西瓜优等品数量较多,所以A技术较好;从平均数的角度看,因A技术种植的西瓜质量的平均数更接近5kg,所以A技术较好;从方差的角度看,因B技术种植的西瓜质量的方差较小,所以B技术种植的西瓜质量更为稳定.从市场销售角度看,因优等品比较畅销,A技术种植的西瓜优等品数量比较多,且平均质量更接近5kg,因而更适合推广A种技术.
课堂小结
课堂小结
抽样调查体现的样本估计总体的数学思想是统计的基本思想,一般是用样本的某些特征估计总体的某些特征.同一组数据,所选取的样本不同,平均数、方差等统计量结果也不相同.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
