冀教版(新)九上-24.2 解一元二次方程 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-24.2 解一元二次方程 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:39 | ||
图片预览








文档简介
(共26张PPT)
24.2 解一元二次方程
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
学校为了美化校园,决定将校园中心边长为 40m的正方形草坪扩展为面积为 2 500m2 的正方形,学校想请小明班的同学计算一下边长应增加多少.许多同学都设边长应增加 xm ,列出方程(40+x)2 =2 500 ,
可是没有人会解这个方程.
小明看了看方程,很快就
求出了方程的解,你想知
道小明是如何用前面所学
的知识解这个方程的吗?
新课精讲
探索新知
1
知识点
二次三项式的配方
例1 用利用完全平方式的特征配方,并完成填空.
(1)x2+10x+________=(x+________)2;
(2)x2+(________)x+ 36=[x+(________)]2;
(3)x2-4x-5=(x-________)2-______.
25
5
±12
±6
2
9
导引:
配方就是要配成完全平方,根据完全平方式的结构特征,当二次项系数为1时,常数项是一次项系数一半的平方.
探索新知
总 结
(1)当二次项系数为1时,已知一次项的系数,则常数项为一次项系数一半的平方;已知常数项,则一次项系数为常数项的平方根的两倍,注意平方根(0除外)有两个.
(2)当二次项系数不为1时,先化二次项系数为1,然后再配方.
典题精讲
1
将代数式a2+4a-5变形,结果正确的是( )
A.(a+2)2-1
B.(a+2)2-5
C.(a+2)2+4
D.(a+2)2-9
D
典题精讲
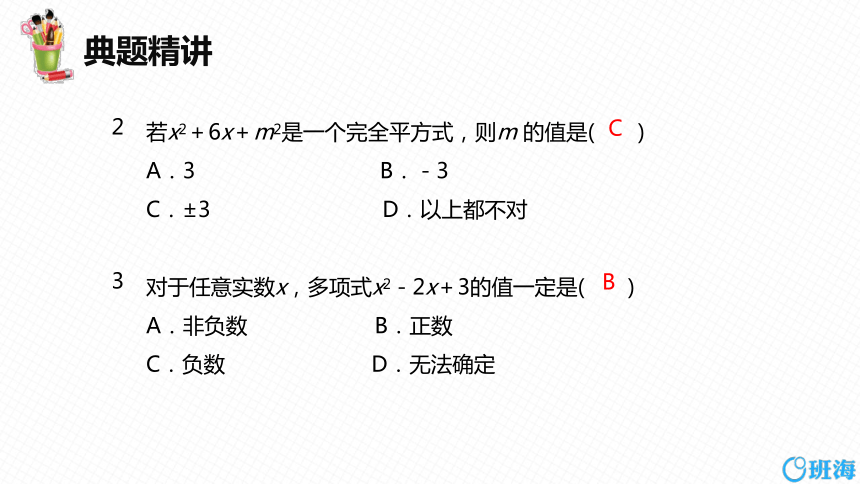
若x2+6x+m2是一个完全平方式,则m 的值是( )
A.3 B.-3
C.±3 D.以上都不对
对于任意实数x,多项式x2-2x+3的值一定是( )
A.非负数 B.正数
C.负数 D.无法确定
2
3
C
B
探索新知
2
知识点
用配方法解一元二次方程
做一做:
先把下列方程化为(x+m)2=n(m,n为常数,且n≥0)的形式,再求出方程的根.
(1)x2+2x=48; (2)x2-4x=12;
(3)x2-6x+5=0; (4)x2+x- =0.
探索新知
归 纳
通过配方,把一元二次方程变形为一边为含未知数的一次式的平方,另一边为常数,当常数为非负数时,利用开平方,将一元二次方程转化为两个 一元一次方程,从而求出原方程的根 . 这种解一元二次方程的方法叫做配方法.
探索新知
例2 用配方法解下列方程.
(1)x2-10x-11=0;
(2)x2+2x-1=0.
解:
(2)移项,得x2+2x=1.
配方,得
x2+2x+12=1+12,
即 (x+1)2=2.
两边开方,得
所以
(1)移项,得
x2-10x=11.
配方,得
x2-10x+52=11+52,
即 (x-5)2=36.
两边开方,得
所以
配方时,先将常 数项移至另一边,再 在方程两边同时加上一 次项系数一半的平方.
探索新知
总 结
用配方法解一元二次方程的步骤:
形如x2+px+q=0型:
第一步移项,把常数项移到右边;
第二步配方,左右两边加上一次项系数一半的平方;
第三步左边写成完全平方式;
第四步,直接开方即可.
探索新知
例3 用配方法解方程:2x2+3=6x.
解:
(1)移项,并将二次项系数化为1,得
x2-3x=
配方,得x2-3x+
即
两边开方,得
所以
探索新知
总 结
对于用配方法解一元二次方程,一般地,首先将二次项系数化为1,并将常数项移到方程的右边,再将方程的两边都加上一次项系数一半的平方,然后写成完全平方的形式,用直接开平方法求得方程的两个根.
典题精讲
2
1
用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A.x2+4x=5 B.2x2-4x=5
C.x2-2x=5 D.x2+2x=5
一元二次方程x2-6x-5=0配方后可变形为( )
A.(x-3)2=14 B.(x-3)2=4
C.(x+3)2=14 D.(x+3)2=4
A
A
典题精讲
下列用配方法解方程2x2-x-6=0,开始出现错误的步骤是( )
2x2-x=6,①
,②
,③
④
A.① B.② C.③ D.④
3
C
学以致用
小试牛刀
1.将二次三项式x +4x+5化成(x+p) +q的形式为
_________________.
(x+2) +1
2.把方程x +4x-5=0化成(x+m) =n的形式,则m,
n 的值分别是( )
A.2,9 B.-2,9
C.2,1 D.-2,1
A
小试牛刀
3.用配方法解方程:2x -4x-8=0.
解:移项,得2x -4x=8.
两边同时除以2,得x -2x=4.
配方,得x -2x=1=4+1,
即(x-1) =5.
∴x-1= ,
∴
小试牛刀
4. 解方程:
(1)x -2x=4.
(2)(x+1)(2x-3)=1.
解:(1)配方,得x -2x+1=4+1,(x-1) =5.由此可得x-1= ,
∴
(2)变形,得x -3x+2x-3=1.化简移项,得2x -x=4.
二次项系数化为1,得
由此可得
小试牛刀
5. 已知实数x满足
解:将原方程两边同时加上2,
得
设
配方,得y +2y+1=2+1,所以(y+1) =3.
直接开平方,得y+1=
解得
小试牛刀
6. 若关于x的方程m(x+h) +k=0(m,h,k均为常数,m≠0)的解是x1=-3, x2=2,求方程m(x+h-3) +k=0的解.
解:由m(x+h) +k=0,得m(x+h) =-k,
∴(x+h) =
∴
解方程m(x+h-3) +k=0,得
课堂小结
课堂小结
直开平方法
降次
配方法
转化
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
24.2 解一元二次方程
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
学校为了美化校园,决定将校园中心边长为 40m的正方形草坪扩展为面积为 2 500m2 的正方形,学校想请小明班的同学计算一下边长应增加多少.许多同学都设边长应增加 xm ,列出方程(40+x)2 =2 500 ,
可是没有人会解这个方程.
小明看了看方程,很快就
求出了方程的解,你想知
道小明是如何用前面所学
的知识解这个方程的吗?
新课精讲
探索新知
1
知识点
二次三项式的配方
例1 用利用完全平方式的特征配方,并完成填空.
(1)x2+10x+________=(x+________)2;
(2)x2+(________)x+ 36=[x+(________)]2;
(3)x2-4x-5=(x-________)2-______.
25
5
±12
±6
2
9
导引:
配方就是要配成完全平方,根据完全平方式的结构特征,当二次项系数为1时,常数项是一次项系数一半的平方.
探索新知
总 结
(1)当二次项系数为1时,已知一次项的系数,则常数项为一次项系数一半的平方;已知常数项,则一次项系数为常数项的平方根的两倍,注意平方根(0除外)有两个.
(2)当二次项系数不为1时,先化二次项系数为1,然后再配方.
典题精讲
1
将代数式a2+4a-5变形,结果正确的是( )
A.(a+2)2-1
B.(a+2)2-5
C.(a+2)2+4
D.(a+2)2-9
D
典题精讲
若x2+6x+m2是一个完全平方式,则m 的值是( )
A.3 B.-3
C.±3 D.以上都不对
对于任意实数x,多项式x2-2x+3的值一定是( )
A.非负数 B.正数
C.负数 D.无法确定
2
3
C
B
探索新知
2
知识点
用配方法解一元二次方程
做一做:
先把下列方程化为(x+m)2=n(m,n为常数,且n≥0)的形式,再求出方程的根.
(1)x2+2x=48; (2)x2-4x=12;
(3)x2-6x+5=0; (4)x2+x- =0.
探索新知
归 纳
通过配方,把一元二次方程变形为一边为含未知数的一次式的平方,另一边为常数,当常数为非负数时,利用开平方,将一元二次方程转化为两个 一元一次方程,从而求出原方程的根 . 这种解一元二次方程的方法叫做配方法.
探索新知
例2 用配方法解下列方程.
(1)x2-10x-11=0;
(2)x2+2x-1=0.
解:
(2)移项,得x2+2x=1.
配方,得
x2+2x+12=1+12,
即 (x+1)2=2.
两边开方,得
所以
(1)移项,得
x2-10x=11.
配方,得
x2-10x+52=11+52,
即 (x-5)2=36.
两边开方,得
所以
配方时,先将常 数项移至另一边,再 在方程两边同时加上一 次项系数一半的平方.
探索新知
总 结
用配方法解一元二次方程的步骤:
形如x2+px+q=0型:
第一步移项,把常数项移到右边;
第二步配方,左右两边加上一次项系数一半的平方;
第三步左边写成完全平方式;
第四步,直接开方即可.
探索新知
例3 用配方法解方程:2x2+3=6x.
解:
(1)移项,并将二次项系数化为1,得
x2-3x=
配方,得x2-3x+
即
两边开方,得
所以
探索新知
总 结
对于用配方法解一元二次方程,一般地,首先将二次项系数化为1,并将常数项移到方程的右边,再将方程的两边都加上一次项系数一半的平方,然后写成完全平方的形式,用直接开平方法求得方程的两个根.
典题精讲
2
1
用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A.x2+4x=5 B.2x2-4x=5
C.x2-2x=5 D.x2+2x=5
一元二次方程x2-6x-5=0配方后可变形为( )
A.(x-3)2=14 B.(x-3)2=4
C.(x+3)2=14 D.(x+3)2=4
A
A
典题精讲
下列用配方法解方程2x2-x-6=0,开始出现错误的步骤是( )
2x2-x=6,①
,②
,③
④
A.① B.② C.③ D.④
3
C
学以致用
小试牛刀
1.将二次三项式x +4x+5化成(x+p) +q的形式为
_________________.
(x+2) +1
2.把方程x +4x-5=0化成(x+m) =n的形式,则m,
n 的值分别是( )
A.2,9 B.-2,9
C.2,1 D.-2,1
A
小试牛刀
3.用配方法解方程:2x -4x-8=0.
解:移项,得2x -4x=8.
两边同时除以2,得x -2x=4.
配方,得x -2x=1=4+1,
即(x-1) =5.
∴x-1= ,
∴
小试牛刀
4. 解方程:
(1)x -2x=4.
(2)(x+1)(2x-3)=1.
解:(1)配方,得x -2x+1=4+1,(x-1) =5.由此可得x-1= ,
∴
(2)变形,得x -3x+2x-3=1.化简移项,得2x -x=4.
二次项系数化为1,得
由此可得
小试牛刀
5. 已知实数x满足
解:将原方程两边同时加上2,
得
设
配方,得y +2y+1=2+1,所以(y+1) =3.
直接开平方,得y+1=
解得
小试牛刀
6. 若关于x的方程m(x+h) +k=0(m,h,k均为常数,m≠0)的解是x1=-3, x2=2,求方程m(x+h-3) +k=0的解.
解:由m(x+h) +k=0,得m(x+h) =-k,
∴(x+h) =
∴
解方程m(x+h-3) +k=0,得
课堂小结
课堂小结
直开平方法
降次
配方法
转化
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
