冀教版(新)九上-25.1 比例线段【优质课件】
文档属性
| 名称 | 冀教版(新)九上-25.1 比例线段【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览









文档简介
(共45张PPT)
25.1 比例线段
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
为了研究相似图形,我们先来探究成比例线段的
有关概念及性质.
新课精讲
探索新知
1
知识点
两条线段的比
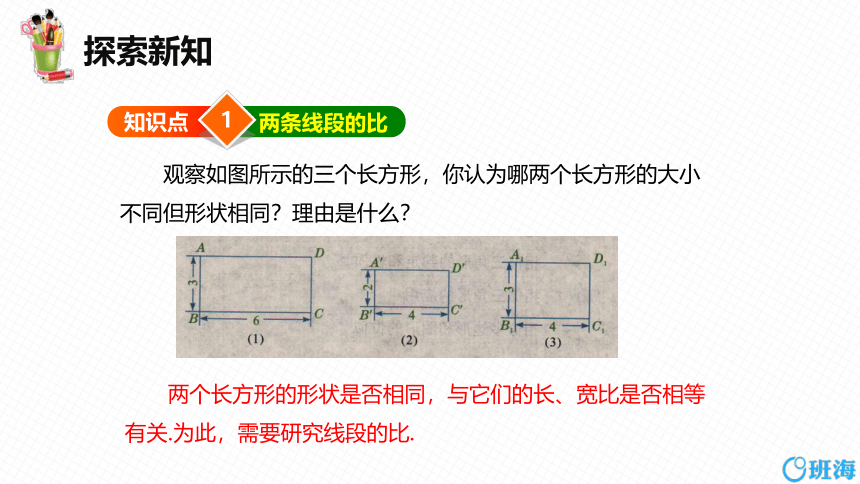
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
两个长方形的形状是否相同,与它们的长、宽比是否相等有关.为此,需要研究线段的比.
探索新知
归 纳
如果选用同一度量单位,量得线段a 和b 的长度分别为m 和n,我们就把m 和n 的比叫做线段a 和b 的比,记作a∶b=m ∶ n,或
例如,如果 a=2 cm,b=3 cm,那么,a∶ b=2∶3.
1.线段的比没有单位;
2.线段的比是一个正数;
3.线段的比与所采用的长度单位无关;
4.线段的比必须是在同一长度单位下进行的.
探索新知
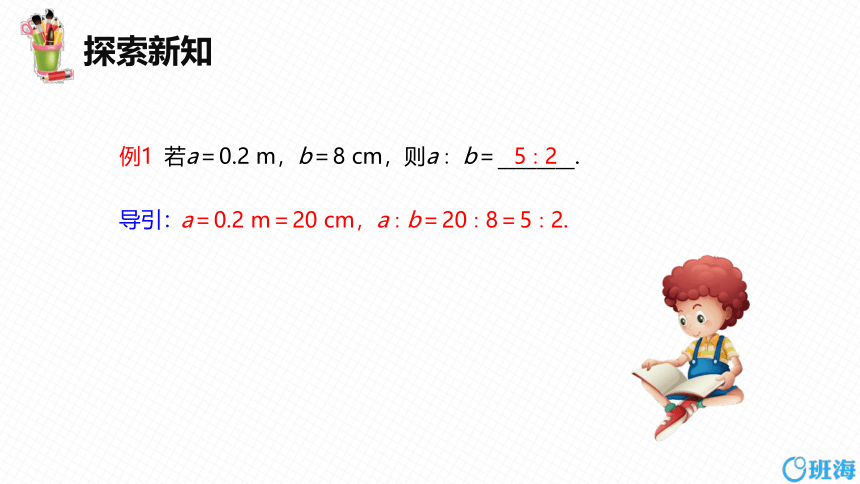
若a=0.2 m,b=8 cm,则a∶ b=________.
例1
导引:
a=0.2 m=20 cm,a∶b=20∶8=5∶2.
5∶2
探索新知
总 结
求线段的比时,两条线段的长度单位应该统一.
典题精讲
1 在比例尺为1 ∶ 5 000的地图上,量得甲、乙两地的距离为25 cm,则甲、乙两地间的实际距离是( )
A.1 250 km B.125 km
C.12.5 km D.1.25 km
D
2 正方形的对角线的长与它的边长之比是( )
A.2∶1 B.1∶2
C.1∶ D. ∶1
D
探索新知
2
知识点
成比例线段
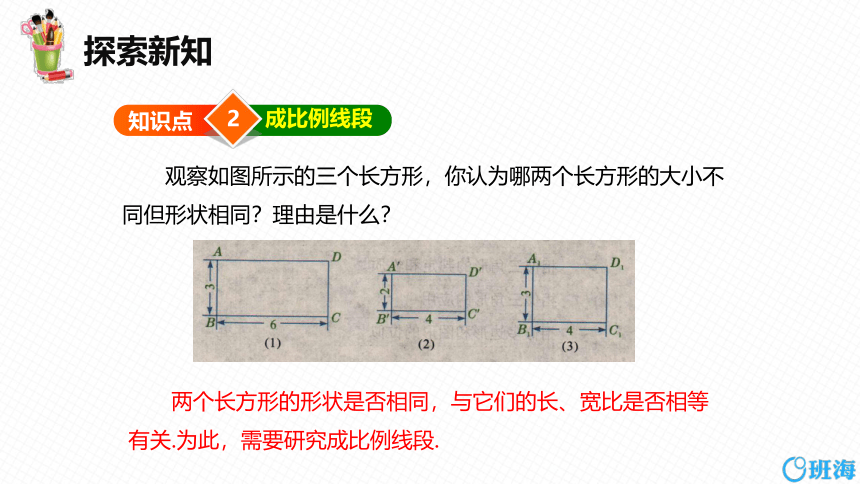
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
两个长方形的形状是否相同,与它们的长、宽比是否相等有关.为此,需要研究成比例线段.
探索新知
1.定义:在四条线段a,b,c,d 中,如果a与b 的比等于c 与d的比,即 我们就把这四条线段叫做成比例线段,简称比例线段.此时也称这四条线段成比例.
2.要点精析:定义中四条线段a,b,c,d 是有先后顺序的.
3.易错提示:计算线段的比时切记不要忽略统一单位.
探索新知
下列各组线段中,能成比例线段的是( )
A.1 cm,3 cm,4 cm,6 cm
B.30 cm,12 cm,0.8 cm,0.2 cm
C.0.1 cm,0.2 cm,0.3 cm,0.4 cm
D.12 cm,16 cm,45 cm,60 cm
例2
D
探索新知
导引:
从比例线段的概念入手.作为选择题,可逐个排查.为了能迅速找到比例关系,可首先对数据按大小排序,以减少试验的次数.
A中的 它们不成比例;
B中的 它们不成比例;
C中的 它们不成比例;
D中的 它们成比例.故选D.
探索新知
方法技巧:
如果说四条线段a、b、c、d 是成比例线段,则这四条线段的顺序就确定了,也就是说,只能写成 这一种形式,而不能写成其它的形式.
探索新知
总 结
判断线段是否成比例,其基本方法是先排序,后求比值,再看比值是否相等.
典题精讲
1 下列四组不同长度的线段中,不是成比例线段的一组是( )
A.1 cm,2 cm,3 cm,6 cm
B.2 cm,3 cm,4 cm,6 cm
C.1 cm,
D.1 cm,2 cm,3 cm,4 cm
D
典题精讲
2 下列各组线段(单位:cm)中,是成比例线段的是( )
A.1,2,3,4 B.1,2,2,4
C.3,5,9,13 D.1,2,2,3
B
3 四条线段a,b,c,d 成比例,其中a=3 cm,d=4 cm,c=6 cm,则b 等于( )
A.8 cm
B. cm
C. cm
D.2 cm
D
如果线段a,b ,c,d 成比例,那么ad 和bc 相等吗 为什么
反之,如果线段a,b ,c,d 满足ad=bc,那么这四条线段成比例吗 为什么
探索新知
3
知识点
比例的性质
探索新知
归 纳
比例的基本性质:
即b2=ac,就把b 叫做a,c 的比例中项.
探索新知
问题:
我们知道,由 可以得到 类
似地,如果 你认为
会有怎样的结果 请说明理由.
探索新知
事实上,若设 则有a=kb,c=kd,···,m=kn.
所以a+c+···+m=kb+kd+···kn+=k(b+d+···+n).
因为b+d+···+n≠0,所以
即
探索新知
若5x-4y=0,则
例3
从比例线段的性质入手. 根据比例的基本性质把5x-
4y=0变形为: 然后利用合比性质变形即得.
也可使用“设参数”的方式,代入后约分即可.
分析:
探索新知
∵5x-4y=0,
∴
∴
令x=4k,y=5k,
则
解:
探索新知
总 结
当有连等式时常用设参数的方法,实际上,当出现比例时,设参数也是非常奏效的方法.
典题精讲
1 若 ,则 等于( )
A. B.
C. D.
2 若 = 的值为( )
A.1 B.
C. D.
B
D
典题精讲
3 如果 的值是( )
A. B.
C. D.
A
探索新知
4
知识点
黄金分割
如图,已知线段AB=a,点C 在AB上.
当 时,线段AC 的长是多少
在上述问题中,设AC=x,建立关于x 的方程x2+ax—a2=0,可解得x= 取其正根,得
C
B
A
探索新知
1.在线段AB上有一点C,如果点C 把AB 分成的两条线段AC 和BC满足 ,那么称线段AB 被点C 黄金分割,点C 称为线段AB的黄金分割点, 称为黄金比.其比值是 近似值是0.618.
2.每条线段上的黄金分割点都有两个.
探索新知
已知线段AB=6 cm,点P 为线段AB 的黄金分割点,则线段AP的长为___________________________.
例4
一条线段有两个黄金分割点,∴要分两种情况计算.
当AP>PB 时, ∵AB=6cm,
∴AP=
当AP<PB 时,PB=
∴AP=AB-PB=(9-3 )cm.
错误答案:
错解分析:
探索新知
总 结
本题运用了分类讨论思想,分AP 是较短线段和较长线段两种情况计算.
探索新知
1 如图所示,点C 把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是( )
A.如果 那么线段AB 被点C 黄金分割
B.如果AC2=AB·BC,那么线段AB 被点C 黄金分割
C.如果线段AB被点C黄金分割,则线段AC 与AB 的比叫做黄金比
D.如果线段AB被点C黄金分割,则 =0.618
D
学以致用
小试牛刀
1.若3y=4x,则下列式子中不正确的是( )
A . B. C. D.
D
2.已知线段a=4,b=16,线段c是线段a,b的比例中项,那么线段c的长为( )
A . 10 B.8 C.-8 D.±8
B
小试牛刀
3. C是线段AB上一点,AB=2AC,则BC∶AB=________.
B
4. 2017 娄底湖南地图出版社首发的竖版《中华人民共和国地图》,将南海诸岛与中国大陆按同比例尺1∶6700000表示出来,使读者能够全面、直观地认识我国版图.若在这种地图上量得我国南北的图上距离是82.09厘米,则我国南北的实际距离大约是________千米(结果精确到1千米).
5500
小试牛刀
5.在人体躯干和身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618越给人以美感.张女士的身高为1.60米,身体躯干(脚底到肚脐的高度)与身高的比值为0.60,那么她穿约________厘米的高跟鞋看起来会更美.(精确到十分位)
6.已知三条线段的长度分别是4,8,5,请写出另一条线段的长度:____________,使这四条线段是成比例线段.
7.5
小试牛刀
7.如图25-1-2①,点C将线段AB分成两部分,若= ,则点C为线段AB的黄金分割点.某研究学习小组,由黄金分割点联想到“黄金分割线”,从而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果= ,那么称直线l为该图形的黄金分割线.
小试牛刀
问题解决:
如图25-1-2②,在△ABC中,已知D是AB的黄金分割点.
(1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组探究发现:过点C作直线交AB于点E,过点D作DF∥CE,交AC于点F,连接EF(如图③),则直线EF也是△ABC的黄金分割线.请你说明理由.
小试牛刀
解:(1)对.理由如下:
∵D 是AB 的黄金分割点,∴
∴直线CD是△ABC 的黄金分割线.
(2)设三角形的面积为S,三角形的中线将三角形分成的两部分的面积为S1,S2,则
∴三角形的中线不是该三角形的黄金分割线.
小试牛刀
(3)∵DF∥CE,∴S△FDE=S△FDC,S△DEC=S△FEC,
∴S△AEF=S△ADC,S四边形BEFC=S△BDC.
∴直线EF 也是△ABC 的黄金分割线.
课堂小结
课堂小结
判断四条线段是否是成比例线段的方法:先将线段长度统一单位并按长度的大小排序,然后,方法1,判断前两条线段的比是否与后两条线段的比相等;方法2,判断最长的线段与最短的线段的乘积是否与另外两条线段的乘积相等.若相等,则这四条线段为成比例线段;若不相等,则这四条线段为不成比例线段.可简记为“一排(排顺序)、二算(算比值或乘积)、三判(判断是否是成比例线段)”.
课堂小结
1.比例的基本性质:如果 那么ad=bc.
比例的基本性质反过来也成立,即:如果ad=bc,那
么 (b,d≠0),也可推得 (c,d≠0).
2.比例中项:如果 即b2=ac,我们就把b叫做a,
c的比例中项.
3.比例还有以下常用性质:
(1)合比性质:如果 那么
(2)分比性质:如果 那么
课堂小结
(3)合分比性质:如果 那么 (a≠b,
c≠d );
(4)等比性质:如果 (b+d+…+n≠0),
那么
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.1 比例线段
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
为了研究相似图形,我们先来探究成比例线段的
有关概念及性质.
新课精讲
探索新知
1
知识点
两条线段的比
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
两个长方形的形状是否相同,与它们的长、宽比是否相等有关.为此,需要研究线段的比.
探索新知
归 纳
如果选用同一度量单位,量得线段a 和b 的长度分别为m 和n,我们就把m 和n 的比叫做线段a 和b 的比,记作a∶b=m ∶ n,或
例如,如果 a=2 cm,b=3 cm,那么,a∶ b=2∶3.
1.线段的比没有单位;
2.线段的比是一个正数;
3.线段的比与所采用的长度单位无关;
4.线段的比必须是在同一长度单位下进行的.
探索新知
若a=0.2 m,b=8 cm,则a∶ b=________.
例1
导引:
a=0.2 m=20 cm,a∶b=20∶8=5∶2.
5∶2
探索新知
总 结
求线段的比时,两条线段的长度单位应该统一.
典题精讲
1 在比例尺为1 ∶ 5 000的地图上,量得甲、乙两地的距离为25 cm,则甲、乙两地间的实际距离是( )
A.1 250 km B.125 km
C.12.5 km D.1.25 km
D
2 正方形的对角线的长与它的边长之比是( )
A.2∶1 B.1∶2
C.1∶ D. ∶1
D
探索新知
2
知识点
成比例线段
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
两个长方形的形状是否相同,与它们的长、宽比是否相等有关.为此,需要研究成比例线段.
探索新知
1.定义:在四条线段a,b,c,d 中,如果a与b 的比等于c 与d的比,即 我们就把这四条线段叫做成比例线段,简称比例线段.此时也称这四条线段成比例.
2.要点精析:定义中四条线段a,b,c,d 是有先后顺序的.
3.易错提示:计算线段的比时切记不要忽略统一单位.
探索新知
下列各组线段中,能成比例线段的是( )
A.1 cm,3 cm,4 cm,6 cm
B.30 cm,12 cm,0.8 cm,0.2 cm
C.0.1 cm,0.2 cm,0.3 cm,0.4 cm
D.12 cm,16 cm,45 cm,60 cm
例2
D
探索新知
导引:
从比例线段的概念入手.作为选择题,可逐个排查.为了能迅速找到比例关系,可首先对数据按大小排序,以减少试验的次数.
A中的 它们不成比例;
B中的 它们不成比例;
C中的 它们不成比例;
D中的 它们成比例.故选D.
探索新知
方法技巧:
如果说四条线段a、b、c、d 是成比例线段,则这四条线段的顺序就确定了,也就是说,只能写成 这一种形式,而不能写成其它的形式.
探索新知
总 结
判断线段是否成比例,其基本方法是先排序,后求比值,再看比值是否相等.
典题精讲
1 下列四组不同长度的线段中,不是成比例线段的一组是( )
A.1 cm,2 cm,3 cm,6 cm
B.2 cm,3 cm,4 cm,6 cm
C.1 cm,
D.1 cm,2 cm,3 cm,4 cm
D
典题精讲
2 下列各组线段(单位:cm)中,是成比例线段的是( )
A.1,2,3,4 B.1,2,2,4
C.3,5,9,13 D.1,2,2,3
B
3 四条线段a,b,c,d 成比例,其中a=3 cm,d=4 cm,c=6 cm,则b 等于( )
A.8 cm
B. cm
C. cm
D.2 cm
D
如果线段a,b ,c,d 成比例,那么ad 和bc 相等吗 为什么
反之,如果线段a,b ,c,d 满足ad=bc,那么这四条线段成比例吗 为什么
探索新知
3
知识点
比例的性质
探索新知
归 纳
比例的基本性质:
即b2=ac,就把b 叫做a,c 的比例中项.
探索新知
问题:
我们知道,由 可以得到 类
似地,如果 你认为
会有怎样的结果 请说明理由.
探索新知
事实上,若设 则有a=kb,c=kd,···,m=kn.
所以a+c+···+m=kb+kd+···kn+=k(b+d+···+n).
因为b+d+···+n≠0,所以
即
探索新知
若5x-4y=0,则
例3
从比例线段的性质入手. 根据比例的基本性质把5x-
4y=0变形为: 然后利用合比性质变形即得.
也可使用“设参数”的方式,代入后约分即可.
分析:
探索新知
∵5x-4y=0,
∴
∴
令x=4k,y=5k,
则
解:
探索新知
总 结
当有连等式时常用设参数的方法,实际上,当出现比例时,设参数也是非常奏效的方法.
典题精讲
1 若 ,则 等于( )
A. B.
C. D.
2 若 = 的值为( )
A.1 B.
C. D.
B
D
典题精讲
3 如果 的值是( )
A. B.
C. D.
A
探索新知
4
知识点
黄金分割
如图,已知线段AB=a,点C 在AB上.
当 时,线段AC 的长是多少
在上述问题中,设AC=x,建立关于x 的方程x2+ax—a2=0,可解得x= 取其正根,得
C
B
A
探索新知
1.在线段AB上有一点C,如果点C 把AB 分成的两条线段AC 和BC满足 ,那么称线段AB 被点C 黄金分割,点C 称为线段AB的黄金分割点, 称为黄金比.其比值是 近似值是0.618.
2.每条线段上的黄金分割点都有两个.
探索新知
已知线段AB=6 cm,点P 为线段AB 的黄金分割点,则线段AP的长为___________________________.
例4
一条线段有两个黄金分割点,∴要分两种情况计算.
当AP>PB 时, ∵AB=6cm,
∴AP=
当AP<PB 时,PB=
∴AP=AB-PB=(9-3 )cm.
错误答案:
错解分析:
探索新知
总 结
本题运用了分类讨论思想,分AP 是较短线段和较长线段两种情况计算.
探索新知
1 如图所示,点C 把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是( )
A.如果 那么线段AB 被点C 黄金分割
B.如果AC2=AB·BC,那么线段AB 被点C 黄金分割
C.如果线段AB被点C黄金分割,则线段AC 与AB 的比叫做黄金比
D.如果线段AB被点C黄金分割,则 =0.618
D
学以致用
小试牛刀
1.若3y=4x,则下列式子中不正确的是( )
A . B. C. D.
D
2.已知线段a=4,b=16,线段c是线段a,b的比例中项,那么线段c的长为( )
A . 10 B.8 C.-8 D.±8
B
小试牛刀
3. C是线段AB上一点,AB=2AC,则BC∶AB=________.
B
4. 2017 娄底湖南地图出版社首发的竖版《中华人民共和国地图》,将南海诸岛与中国大陆按同比例尺1∶6700000表示出来,使读者能够全面、直观地认识我国版图.若在这种地图上量得我国南北的图上距离是82.09厘米,则我国南北的实际距离大约是________千米(结果精确到1千米).
5500
小试牛刀
5.在人体躯干和身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618越给人以美感.张女士的身高为1.60米,身体躯干(脚底到肚脐的高度)与身高的比值为0.60,那么她穿约________厘米的高跟鞋看起来会更美.(精确到十分位)
6.已知三条线段的长度分别是4,8,5,请写出另一条线段的长度:____________,使这四条线段是成比例线段.
7.5
小试牛刀
7.如图25-1-2①,点C将线段AB分成两部分,若= ,则点C为线段AB的黄金分割点.某研究学习小组,由黄金分割点联想到“黄金分割线”,从而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果= ,那么称直线l为该图形的黄金分割线.
小试牛刀
问题解决:
如图25-1-2②,在△ABC中,已知D是AB的黄金分割点.
(1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组探究发现:过点C作直线交AB于点E,过点D作DF∥CE,交AC于点F,连接EF(如图③),则直线EF也是△ABC的黄金分割线.请你说明理由.
小试牛刀
解:(1)对.理由如下:
∵D 是AB 的黄金分割点,∴
∴直线CD是△ABC 的黄金分割线.
(2)设三角形的面积为S,三角形的中线将三角形分成的两部分的面积为S1,S2,则
∴三角形的中线不是该三角形的黄金分割线.
小试牛刀
(3)∵DF∥CE,∴S△FDE=S△FDC,S△DEC=S△FEC,
∴S△AEF=S△ADC,S四边形BEFC=S△BDC.
∴直线EF 也是△ABC 的黄金分割线.
课堂小结
课堂小结
判断四条线段是否是成比例线段的方法:先将线段长度统一单位并按长度的大小排序,然后,方法1,判断前两条线段的比是否与后两条线段的比相等;方法2,判断最长的线段与最短的线段的乘积是否与另外两条线段的乘积相等.若相等,则这四条线段为成比例线段;若不相等,则这四条线段为不成比例线段.可简记为“一排(排顺序)、二算(算比值或乘积)、三判(判断是否是成比例线段)”.
课堂小结
1.比例的基本性质:如果 那么ad=bc.
比例的基本性质反过来也成立,即:如果ad=bc,那
么 (b,d≠0),也可推得 (c,d≠0).
2.比例中项:如果 即b2=ac,我们就把b叫做a,
c的比例中项.
3.比例还有以下常用性质:
(1)合比性质:如果 那么
(2)分比性质:如果 那么
课堂小结
(3)合分比性质:如果 那么 (a≠b,
c≠d );
(4)等比性质:如果 (b+d+…+n≠0),
那么
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
