冀教版(新)九上-25.2 平行线分线段成比例 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-25.2 平行线分线段成比例 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:39 | ||
图片预览







文档简介
(共31张PPT)
25.2 平行线分线段成比例
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.使学生在理解的基础上掌握平行线分线段成比例定理及其推论,并会灵活应用.
2.使学生掌握三角形一边平行线的判定定理.
3.已知线的成已知比的作图问题.
4.通过应用,培养识图能力和推理论证能力.
5.通过定理的教学,进一步培养学生类比的数学思想.
新课精讲
探索新知
1
类型
证比例式
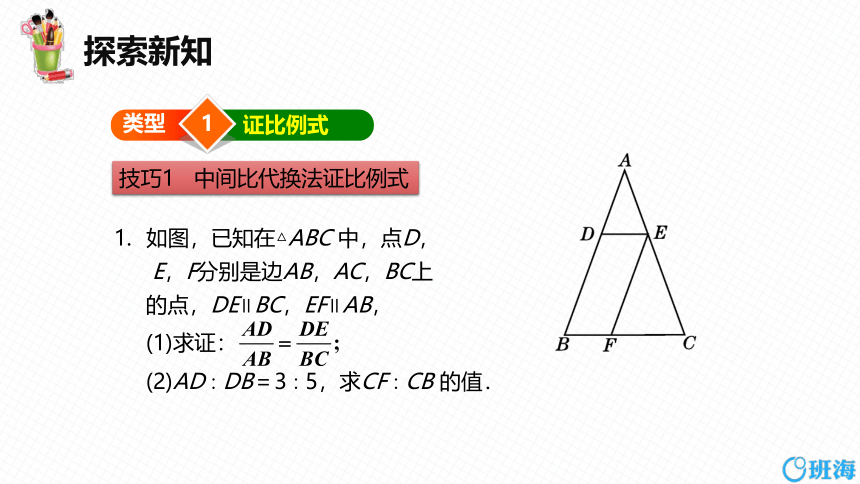
技巧1 中间比代换法证比例式
如图,已知在△ABC 中,点D,
E,F分别是边AB,AC,BC上
的点,DE∥BC,EF∥AB,
(1)求证:
(2)AD∶DB=3∶5,求CF∶CB 的值.
探索新知
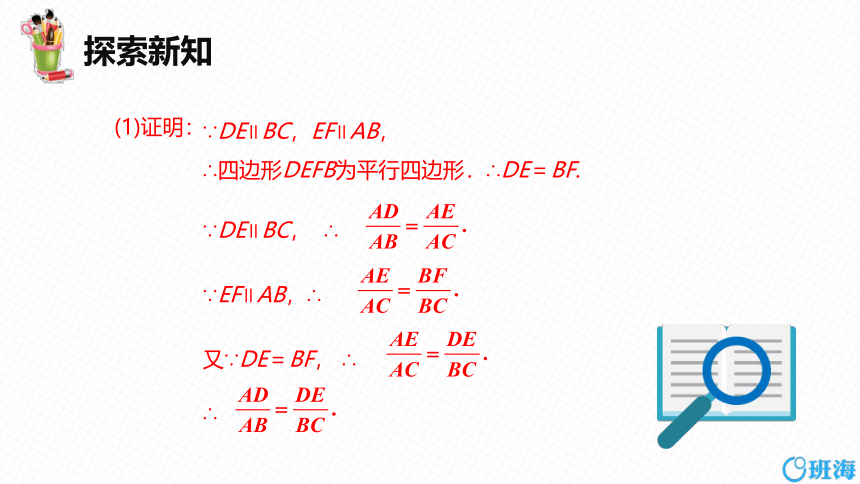
∵DE∥BC,EF∥AB,
∴四边形DEFB为平行四边形.∴DE=BF.
∵DE∥BC, ∴
∵EF∥AB,∴
又∵DE=BF, ∴
∴
(1)证明:
探索新知
∵AD∶DB=3∶5,
∴BD∶AB=5∶8.
∵DE∥BC,
∴CE∶AC=BD∶AB=5∶8.
∵EF∥AB,
∴CF∶CB=CE∶AC=5∶8.
(2)解:
探索新知
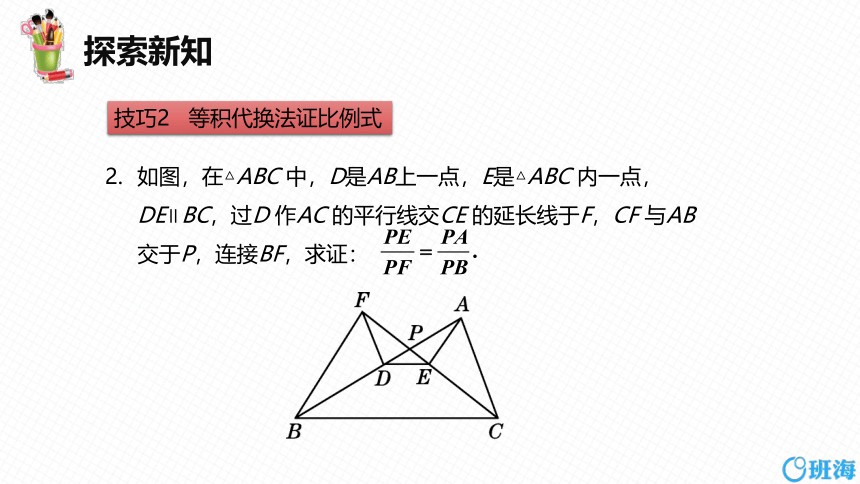
技巧2 等积代换法证比例式
如图,在△ABC 中,D是AB上一点,E是△ABC 内一点,DE∥BC,过D 作AC 的平行线交CE 的延长线于F,CF 与AB交于P,连接BF,求证:
探索新知
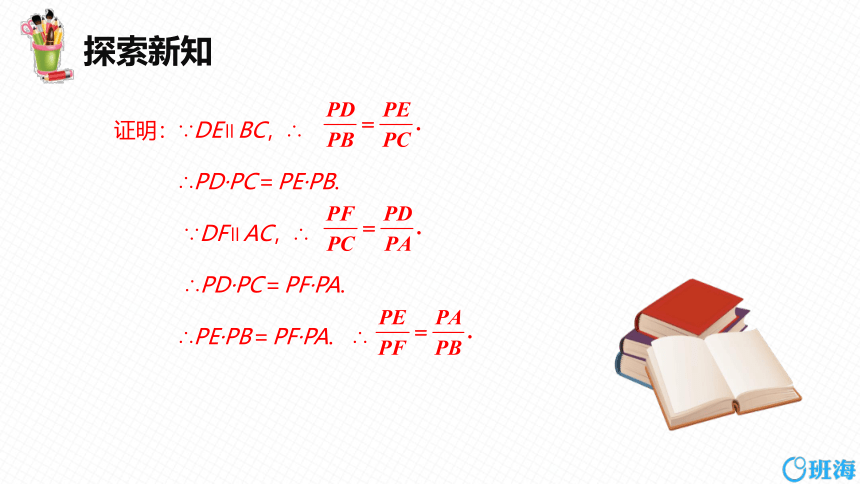
证明:∵DE∥BC,∴
∴PD·PC=PE·PB.
∵DF∥AC,∴
∴PD·PC=PF·PA.
∴PE·PB=PF·PA. ∴
探索新知
技巧3 等比代换法证比例中项
如图,在△ABC 中,DE∥BC,EF∥CD.
求证:
证明:∵EF∥CD,
∴
∵DE∥BC. ∴
∴
探索新知
技巧4 平行法证比例式
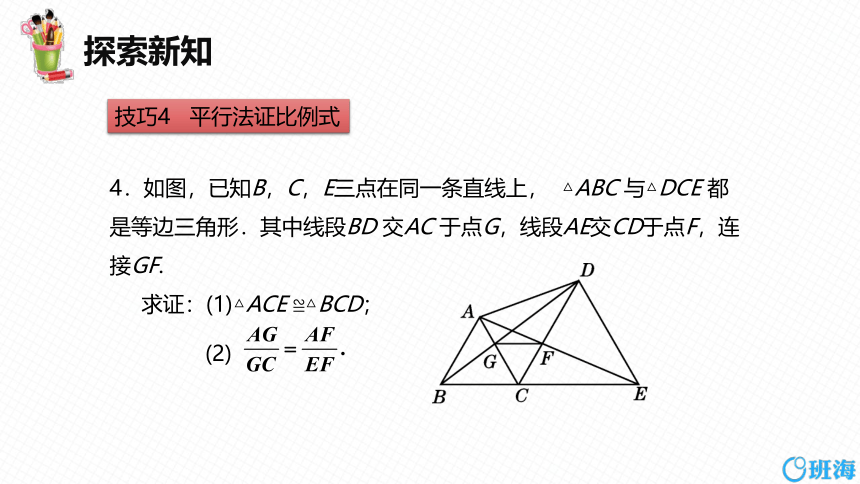
4.如图,已知B,C,E三点在同一条直线上, △ABC 与△DCE 都是等边三角形.其中线段BD 交AC 于点G,线段AE交CD于点F,连接GF.
求证:(1)△ACE ≌△BCD;
(2)
探索新知
(1)∵△ABC 与△DCE 都是等边三角形,
∴AC=BC,CE=CD,
∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD.
∴△ACE ≌△BCD (SAS).
证明:
探索新知
(2)∵△ACE ≌△BCD,
∴∠BDC=∠AEC.
又∵∠GCD=180°-∠ACB-∠DCE
=60°=∠FCE,CD=CE,
∴△GCD ≌△FCE(ASA).
∴CG=CF. ∴△CFG 为等边三角形.
∴∠CGF=∠ACB=60°.
∴GF∥CE. ∴
探索新知
2
类型
证线段相等
技巧5 等比例过渡法证线段相等(等比例过渡法)
5. 如图,在△ABC 中,∠ACB=90°,∠B>∠A,
点D为边AB 的中点,DE∥BC 交AC 于点E,
CF∥BA交DE 的延长线于点F.
求证:DE=EF.
探索新知
证明:∵DE∥BC,∴
∵点D为AB 的中点,
∴AD=DB,即
∵CF∥BA,
∴
∴DE=EF.
探索新知
3
类型
证比例和为1
技巧6 同分母的中间比代换法
6. 如图,已知AC∥FE∥BD,求证:
探索新知
∵AC∥EF,
∴ ①.
又∵FE∥BD,
∴ ② .
①+②,得
即
证明:
学以致用
小试牛刀
1.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
AB =AC BC B. C =AC BC
C. ACBC D. BCAB
D
2. 在比例尺为1:10000000的地图上,量的甲、乙两地的距离是30cm,则两地的实际距离是( )
A. 30km B. 300km C. 3000km D. 30000km
C
小试牛刀
3.如图,中,D,E 两点分别在AB,AC 边上,且,如果,AC=6,那么AE 的长为
A. 3 B. 4 C. 9 D. 12
B
4.如图所示,,AC 与BD 相交于点E,若,,,则 的值是______.
小试牛刀
5. 甲、乙两地有一段20km的铁路,在比例尺为1:500000的地图中,这段铁路应画__________ cm.
6. 在比例尺为1:400000的地图上,某条道路的长为7cm,则该道路的实际长度是______km.
4
28
小试牛刀
7.如图,已知B,C,E三点在同一条直线上,△ABC与△DCE 都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F,连接GF.
求证:(1)△ACE≌△BCD;
(2)
小试牛刀
证明:
∵△ABC 与△DCE 都是等边三角形,
∴AC=BC,CE=CD,∠DCE=∠ACB=60°.
∴∠DCE+∠ACD=∠ACB+∠ACD,
即∠ACE=∠BCD.
∴△ACE ≌△BCD (SAS).
(1)△ACE≌△BCD;
小试牛刀
(2)
证明:
∵△ACE≌△BCD,∴∠BDC=∠AEC.
又∵∠GCD=180°-∠ACB-∠DCE=60°=∠FCE,
CD=CE,
∴△GCD≌△FCE (ASA).∴CG=CF.
∴△CFG为等边三角形.∴∠CFG=∠DCE=60°.
∴GF∥CE.∴
小试牛刀
8.如图,已知在△ABC中,D,E,F 分别是边AB,AC,BC上的点,DE∥BC,EF∥AB.
(1)求证: ;
(2)若AD∶DB=3∶5,求CF∶CB 的值.
小试牛刀
(1)求证: ;
证明:
∵DE∥BC,EF∥AB,
∴四边形DEFB为平行四边形.∴DE=BF.
∵DE∥BC,∴
∵EF∥AB,∴
又∵DE=BF,∴
∴
小试牛刀
解:
∵AD∶DB=3∶5,
∴BD∶AB=5∶8.
∵DE∥BC,
∴CE∶AC=BD∶AB=5∶8.
∵EF∥AB,
∴CF∶CB=CE∶AC=5∶8.
(2)若AD∶DB=3∶5,求CF∶CB的值.
课堂小结
课堂小结
利用平行线证比例式或等积式的方法:
当比例式或等积式中线段不在平行线上,若平行线为一组(两条以上)时,可直接利用平行线分线段成比例的基本事实证明;若平行线只有两条时,则利用平行线分线段成比例的基本事实的推论证明;当比例式或等积式中的线段不是对应线段时,则利用转化思想,用等线段、等比例、等积替换进行论证.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.2 平行线分线段成比例
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.使学生在理解的基础上掌握平行线分线段成比例定理及其推论,并会灵活应用.
2.使学生掌握三角形一边平行线的判定定理.
3.已知线的成已知比的作图问题.
4.通过应用,培养识图能力和推理论证能力.
5.通过定理的教学,进一步培养学生类比的数学思想.
新课精讲
探索新知
1
类型
证比例式
技巧1 中间比代换法证比例式
如图,已知在△ABC 中,点D,
E,F分别是边AB,AC,BC上
的点,DE∥BC,EF∥AB,
(1)求证:
(2)AD∶DB=3∶5,求CF∶CB 的值.
探索新知
∵DE∥BC,EF∥AB,
∴四边形DEFB为平行四边形.∴DE=BF.
∵DE∥BC, ∴
∵EF∥AB,∴
又∵DE=BF, ∴
∴
(1)证明:
探索新知
∵AD∶DB=3∶5,
∴BD∶AB=5∶8.
∵DE∥BC,
∴CE∶AC=BD∶AB=5∶8.
∵EF∥AB,
∴CF∶CB=CE∶AC=5∶8.
(2)解:
探索新知
技巧2 等积代换法证比例式
如图,在△ABC 中,D是AB上一点,E是△ABC 内一点,DE∥BC,过D 作AC 的平行线交CE 的延长线于F,CF 与AB交于P,连接BF,求证:
探索新知
证明:∵DE∥BC,∴
∴PD·PC=PE·PB.
∵DF∥AC,∴
∴PD·PC=PF·PA.
∴PE·PB=PF·PA. ∴
探索新知
技巧3 等比代换法证比例中项
如图,在△ABC 中,DE∥BC,EF∥CD.
求证:
证明:∵EF∥CD,
∴
∵DE∥BC. ∴
∴
探索新知
技巧4 平行法证比例式
4.如图,已知B,C,E三点在同一条直线上, △ABC 与△DCE 都是等边三角形.其中线段BD 交AC 于点G,线段AE交CD于点F,连接GF.
求证:(1)△ACE ≌△BCD;
(2)
探索新知
(1)∵△ABC 与△DCE 都是等边三角形,
∴AC=BC,CE=CD,
∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD.
∴△ACE ≌△BCD (SAS).
证明:
探索新知
(2)∵△ACE ≌△BCD,
∴∠BDC=∠AEC.
又∵∠GCD=180°-∠ACB-∠DCE
=60°=∠FCE,CD=CE,
∴△GCD ≌△FCE(ASA).
∴CG=CF. ∴△CFG 为等边三角形.
∴∠CGF=∠ACB=60°.
∴GF∥CE. ∴
探索新知
2
类型
证线段相等
技巧5 等比例过渡法证线段相等(等比例过渡法)
5. 如图,在△ABC 中,∠ACB=90°,∠B>∠A,
点D为边AB 的中点,DE∥BC 交AC 于点E,
CF∥BA交DE 的延长线于点F.
求证:DE=EF.
探索新知
证明:∵DE∥BC,∴
∵点D为AB 的中点,
∴AD=DB,即
∵CF∥BA,
∴
∴DE=EF.
探索新知
3
类型
证比例和为1
技巧6 同分母的中间比代换法
6. 如图,已知AC∥FE∥BD,求证:
探索新知
∵AC∥EF,
∴ ①.
又∵FE∥BD,
∴ ② .
①+②,得
即
证明:
学以致用
小试牛刀
1.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是( )
AB =AC BC B. C =AC BC
C. ACBC D. BCAB
D
2. 在比例尺为1:10000000的地图上,量的甲、乙两地的距离是30cm,则两地的实际距离是( )
A. 30km B. 300km C. 3000km D. 30000km
C
小试牛刀
3.如图,中,D,E 两点分别在AB,AC 边上,且,如果,AC=6,那么AE 的长为
A. 3 B. 4 C. 9 D. 12
B
4.如图所示,,AC 与BD 相交于点E,若,,,则 的值是______.
小试牛刀
5. 甲、乙两地有一段20km的铁路,在比例尺为1:500000的地图中,这段铁路应画__________ cm.
6. 在比例尺为1:400000的地图上,某条道路的长为7cm,则该道路的实际长度是______km.
4
28
小试牛刀
7.如图,已知B,C,E三点在同一条直线上,△ABC与△DCE 都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F,连接GF.
求证:(1)△ACE≌△BCD;
(2)
小试牛刀
证明:
∵△ABC 与△DCE 都是等边三角形,
∴AC=BC,CE=CD,∠DCE=∠ACB=60°.
∴∠DCE+∠ACD=∠ACB+∠ACD,
即∠ACE=∠BCD.
∴△ACE ≌△BCD (SAS).
(1)△ACE≌△BCD;
小试牛刀
(2)
证明:
∵△ACE≌△BCD,∴∠BDC=∠AEC.
又∵∠GCD=180°-∠ACB-∠DCE=60°=∠FCE,
CD=CE,
∴△GCD≌△FCE (ASA).∴CG=CF.
∴△CFG为等边三角形.∴∠CFG=∠DCE=60°.
∴GF∥CE.∴
小试牛刀
8.如图,已知在△ABC中,D,E,F 分别是边AB,AC,BC上的点,DE∥BC,EF∥AB.
(1)求证: ;
(2)若AD∶DB=3∶5,求CF∶CB 的值.
小试牛刀
(1)求证: ;
证明:
∵DE∥BC,EF∥AB,
∴四边形DEFB为平行四边形.∴DE=BF.
∵DE∥BC,∴
∵EF∥AB,∴
又∵DE=BF,∴
∴
小试牛刀
解:
∵AD∶DB=3∶5,
∴BD∶AB=5∶8.
∵DE∥BC,
∴CE∶AC=BD∶AB=5∶8.
∵EF∥AB,
∴CF∶CB=CE∶AC=5∶8.
(2)若AD∶DB=3∶5,求CF∶CB的值.
课堂小结
课堂小结
利用平行线证比例式或等积式的方法:
当比例式或等积式中线段不在平行线上,若平行线为一组(两条以上)时,可直接利用平行线分线段成比例的基本事实证明;若平行线只有两条时,则利用平行线分线段成比例的基本事实的推论证明;当比例式或等积式中的线段不是对应线段时,则利用转化思想,用等线段、等比例、等积替换进行论证.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
