冀教版(新)九上-25.3 相似三角形【优质课件】
文档属性
| 名称 | 冀教版(新)九上-25.3 相似三角形【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:39 | ||
图片预览









文档简介
(共43张PPT)
25.3 相似三角形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
对应角相等、对应边也相等的两个三角形为全等三角形.相仿地,我们来学习相似三角形的有关知识.
新课精讲
探索新知
1
知识点
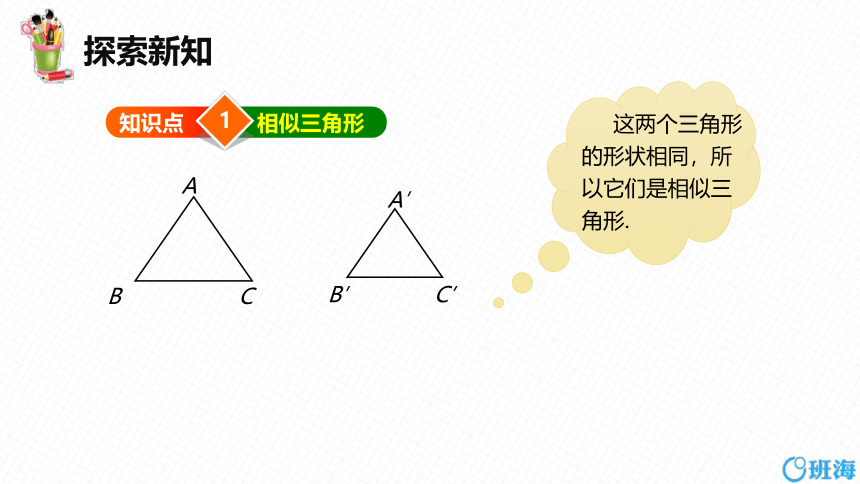
相似三角形
这两个三角形的形状相同,所以它们是相似三角形.
B
C
A
B′
C′
A′
探索新知
归 纳
对应角相等、对应边成比例的两个三角形叫做相似三角形(similar triangles).相似三角形对应边的比叫做它们的相似比(similar ratio) .
探索新知
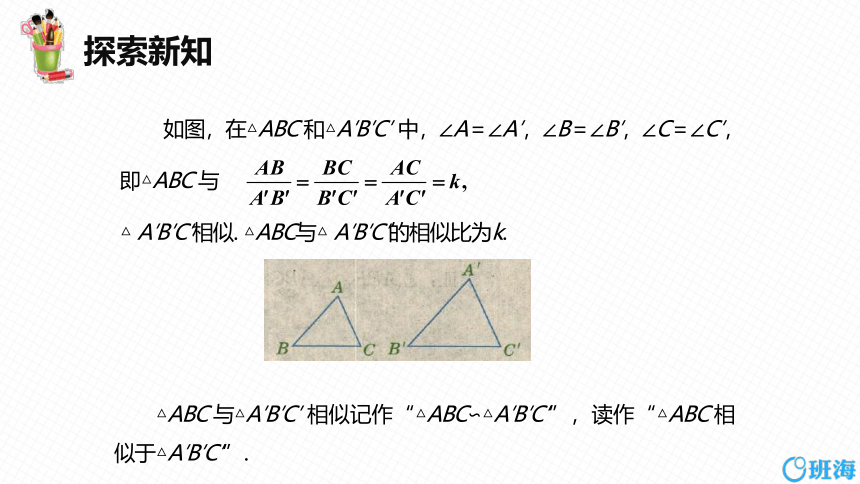
如图,在△ABC 和△A′B′C′ 中,∠A=∠A′,∠B=∠B′,∠C=∠C′, 即△ABC 与
△ A′B′C′相似. △ABC与△ A′B′C′的相似比为k.
△ABC 与△A′B′C′ 相似记作“△ABC∽△A′B′C′”,读作“△ABC 相似于△A′B′C′”.
探索新知
1.要点精析:
(1)若两个三角形相似,则三个角分别相等,三条边成比例;
(2)相似三角形具有传递性:即
若△ABC∽△A′B′C′,△A′B′C′∽△A″B″C″,
则△ABC∽△A″B″C″;
(3)相似比为1的两个相似三角形全等,反过来两个全等三角形是相似比为1的相似三角形.
探索新知
2.易错警示:
(1)对应性:表示两三角形相似时,要注意对应性,即
要把对应顶点的字母写在对应位置上.
(2)顺序性:求两相似三角形的相似比时,要注意顺序
性.若当△ABC∽△A′B′C′时,
则△A′B′C′∽△ABC时,
探索新知
如图,△AEF∽△ABC.
(1)若AE=3,AB=5,EF=2.4,求BC 的长.
(2)求证:EF∥BC.
(1)∵△AEF∽△ABC,
∴
又∵AE=3,AB=5,EF=2.4,
∴
例1
解:
探索新知
(2)∵△AEF∽△ABC,
∴∠AEF=∠B.
∴BF∥BC.
探索新知
总 结
根据相似三角形的定义进行判断,即证出三个角
分别相等,三条边成比例即可.
典题精讲
1 如图,已知点D,E 分别在△ABC 的边AC,AB上,△ADE∽△ABC,AD=6,DC=2,AE=4,EB=8,则△ABC 与△ADE 的相似比是__________,△ADE 与△ABC 的相似比是__________.
2:1
1:2
典题精讲
2 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C 等于( )
A.40°
B.60°
C.80°
D.100°
C
典题精讲
3 如图,△ABC∽△DEF,相似比为1∶2.若BC=1,则EF 的长是( )
A.1
B.2
C.3
D.4
B
探索新知
2
知识点
平行线判定三角形相似
思考
如图,在△ABC 中,DE∥BC,且DE 分别交AB,AC 于点D,E,△ADE与△ABC有什么关系?
探索新知
我们知道,平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.进而可知,这样截得的三角形与原三角形相似.
已知:如图, EF∥BC,与AB,AC(或它们的延长线)相交于点E, F.
求证:△AEF∽△ABC.
探索新知
证明:
如图(1),在△AEF 和△ABC 中,
∵EF∥BC,
∴∠AEF=∠B,
∠AFE=∠C,
且
又∵∠A=∠A,
∴△AEF∽△ABC.
同理可证其他情况.
探索新知
归 纳
平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.
探索新知
如图,在 ABCD中,F 是AD 边上的任意一点,连接BF 并延长交CD 的延长线于点E,连接AC,则图中与△DEF 相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个
例2
B
证明:
由于四边形ABCD是平行四边形,因此FD∥BC,DE∥AB.于是可从图中找出符合“A”型相似的△DEF 与△CEB,符合“X”型相似的△DEF与△ABF.故选B.
探索新知
总 结
利用平行线寻找相似三角形的方法:在线段较多的图形中寻找相似三角形,如果图中有线段平行的条件,则集中精力在图形中寻找符合“A”型或“X”型的基本图形,这不但是解本题的首要之选,也是今后解本类题目的首要之选.
典题精讲
1 如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:
①BC=2DE;②△ADE∽△ABC;③
其中正确的有( )
A.3个
B.2个
C.1个
D.0个
A
典题精讲
2 如图,已知AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.3对
C.2对
D.1对
B
探索新知
3
知识点
相似三角形性质的应用
如图所示,要测量一个池塘的
长是多少,不能直接测量的距离,
小明做了△ABC,取池塘的两个点
D,E,使DE∥BC,测出BC,AD,
AB 的长就可以算出DE 的长,你知道为什么吗?
原来由DE∥BC 可以得到△ABC∽△ADE,
所以AD∶AB=DE∶BC
探索新知
归 纳
通过建立相似三角形数学模型可以解决实际问题。
探索新知
如图,在 ABCD 中,AE=EB,AF=2,则FC=________.
例3
4
探索新知
导引:
有平行四边形,就提供了平行线,就有三角形相
似,就有对应边的比相等,就能求出FC 的长.
在 ABCD 中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∴
∵AE=EB,∴
∴FC=2AF=4
探索新知
总 结
求线段的长的方法:对于三角形被平行线所截形成“A”型或“X”型的图形,当所求的线段或已知线段在平行的边上时,通常考虑通过找三角形相似,再利用相似三角形的对应边的比相等构建包含已知与未知线段的比例式,即可求出线段的长;当所求的线段或已知线段不在平行的边上时,则考虑直接用平行线截线段成比例求线段的长.
典题精讲
1 如图,已知AB,CD,EF 都与BD 垂直,垂足分别是B,D,F,且AB=1,CD=3,那么EF 的长是( )
A.
B.
C.
D.
C
典题精讲
2 如图,AB∥CD,AD与BC 相交于点O,那么在下列比例式中,正确的是( )
A.
B.
C.
D.
C
典题精讲
3 如图,在△ABC中,DE∥BC,AE ∶ EC=2 ∶ 3,DE=4,则BC 等于( )
A.10
B.8
C.9
D.6
A
学以致用
小试牛刀
1.在△ABC 中,已知AB=5,BC=4,AC=8.若△ABC∽△A1B1C1,△A1B1C1的最长边的长为16,则其他两边的长分别为( )
A . A1B1=8,B1C1=10
B.A1B1=10,B1C1=8
C.A1B1=5,B1C1=8
D.A1B1=10,B1C1=4
B
小试牛刀
2.已知△ABC∽△A1B1C1,且A1B1=6 cm,AB=4 cm,BC=3.2 cm,∠B=58°,∠C=72°,则B1C1=________cm,∠A1=________°.
4.8
50
3.如果△ABC∽△DEF,且△ABC与△DEF的相似比为k1,△DEF 与△ABC的相似比为k2,则k1与k2的关系是( )
A.k1=k2 B.k1+k2=0
C.k1·k2=-1 D .k1·k2=1
D
小试牛刀
4.如图,在 ABCD 中,M,N 为对角线BD 的三等分点,连接AM 并延长交BC于点E,连接EN并延长交AD于点F.
(1)求证:△AMD∽△EMB;
(2)求 的值.
小试牛刀
(1)证明:∵四边形ABCD 为平行四边形,
∴AD∥BE. ∴△AMD∽△EMB.
(2) ∵AD∥BC,∴△FND∽△ENB.
∴
∵M,N 为BD 的三等分点,∴
∴
小试牛刀
5.如图,在 ABCD 中,点E在边BC 上,点F在边AD 的延长线上,且DF=BE.EF 与CD 交于点G.
(1)求证:BD∥EF;
(2)若 ,BE=4,求EC 的长.
小试牛刀
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵DF=BE,
∴四边形BEFD是平行四边形,
∴BD∥EF.
(2) ∵BE=4,∴DF=4.
∵DF∥EC,
∴△DFG∽△CEG,∴
∴EC=
课堂小结
课堂小结
1.相似三角形的定义具有两种功能:
判定和性质,即对应边成比例、对应角相等 两个三角形相似,注意相似比具有顺序性.
2.平行线截三角形相似的定理:
平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.数学表达式:如图,∵DE∥BC,
∴△ABC∽△ADE.
课堂小结
要点精析:根据定
理得到的相似三角
形的三个基本图形
中都有BC∥DE,图(1)(2)很像大写字母A,故我们称
之为“A”型相似;图(3)很像大写字母X,故我们称之为“X”型相似(也像阿拉伯数字“8”).
3.作用:本定理是相似三角形判定定理的预备定理:它通过平行证三角形相似,再由相似证对应角相等、对应边成比例.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.3 相似三角形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
对应角相等、对应边也相等的两个三角形为全等三角形.相仿地,我们来学习相似三角形的有关知识.
新课精讲
探索新知
1
知识点
相似三角形
这两个三角形的形状相同,所以它们是相似三角形.
B
C
A
B′
C′
A′
探索新知
归 纳
对应角相等、对应边成比例的两个三角形叫做相似三角形(similar triangles).相似三角形对应边的比叫做它们的相似比(similar ratio) .
探索新知
如图,在△ABC 和△A′B′C′ 中,∠A=∠A′,∠B=∠B′,∠C=∠C′, 即△ABC 与
△ A′B′C′相似. △ABC与△ A′B′C′的相似比为k.
△ABC 与△A′B′C′ 相似记作“△ABC∽△A′B′C′”,读作“△ABC 相似于△A′B′C′”.
探索新知
1.要点精析:
(1)若两个三角形相似,则三个角分别相等,三条边成比例;
(2)相似三角形具有传递性:即
若△ABC∽△A′B′C′,△A′B′C′∽△A″B″C″,
则△ABC∽△A″B″C″;
(3)相似比为1的两个相似三角形全等,反过来两个全等三角形是相似比为1的相似三角形.
探索新知
2.易错警示:
(1)对应性:表示两三角形相似时,要注意对应性,即
要把对应顶点的字母写在对应位置上.
(2)顺序性:求两相似三角形的相似比时,要注意顺序
性.若当△ABC∽△A′B′C′时,
则△A′B′C′∽△ABC时,
探索新知
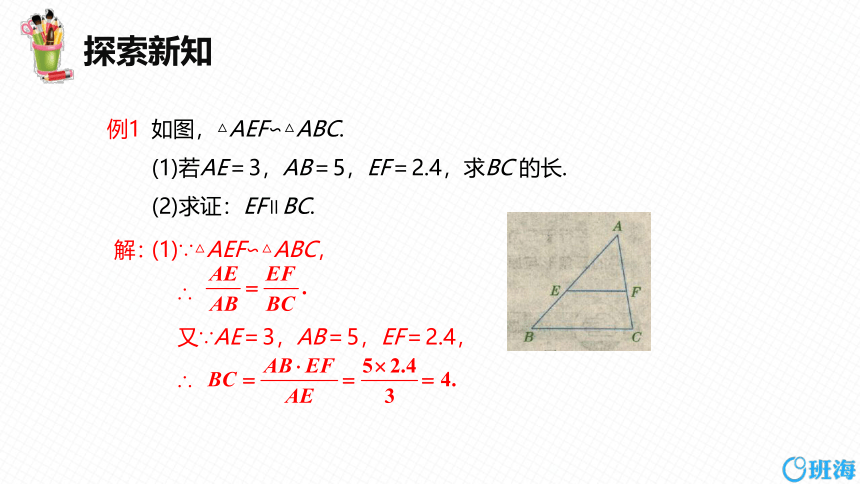
如图,△AEF∽△ABC.
(1)若AE=3,AB=5,EF=2.4,求BC 的长.
(2)求证:EF∥BC.
(1)∵△AEF∽△ABC,
∴
又∵AE=3,AB=5,EF=2.4,
∴
例1
解:
探索新知
(2)∵△AEF∽△ABC,
∴∠AEF=∠B.
∴BF∥BC.
探索新知
总 结
根据相似三角形的定义进行判断,即证出三个角
分别相等,三条边成比例即可.
典题精讲
1 如图,已知点D,E 分别在△ABC 的边AC,AB上,△ADE∽△ABC,AD=6,DC=2,AE=4,EB=8,则△ABC 与△ADE 的相似比是__________,△ADE 与△ABC 的相似比是__________.
2:1
1:2
典题精讲
2 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C 等于( )
A.40°
B.60°
C.80°
D.100°
C
典题精讲
3 如图,△ABC∽△DEF,相似比为1∶2.若BC=1,则EF 的长是( )
A.1
B.2
C.3
D.4
B
探索新知
2
知识点
平行线判定三角形相似
思考
如图,在△ABC 中,DE∥BC,且DE 分别交AB,AC 于点D,E,△ADE与△ABC有什么关系?
探索新知
我们知道,平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.进而可知,这样截得的三角形与原三角形相似.
已知:如图, EF∥BC,与AB,AC(或它们的延长线)相交于点E, F.
求证:△AEF∽△ABC.
探索新知
证明:
如图(1),在△AEF 和△ABC 中,
∵EF∥BC,
∴∠AEF=∠B,
∠AFE=∠C,
且
又∵∠A=∠A,
∴△AEF∽△ABC.
同理可证其他情况.
探索新知
归 纳
平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.
探索新知
如图,在 ABCD中,F 是AD 边上的任意一点,连接BF 并延长交CD 的延长线于点E,连接AC,则图中与△DEF 相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个
例2
B
证明:
由于四边形ABCD是平行四边形,因此FD∥BC,DE∥AB.于是可从图中找出符合“A”型相似的△DEF 与△CEB,符合“X”型相似的△DEF与△ABF.故选B.
探索新知
总 结
利用平行线寻找相似三角形的方法:在线段较多的图形中寻找相似三角形,如果图中有线段平行的条件,则集中精力在图形中寻找符合“A”型或“X”型的基本图形,这不但是解本题的首要之选,也是今后解本类题目的首要之选.
典题精讲
1 如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:
①BC=2DE;②△ADE∽△ABC;③
其中正确的有( )
A.3个
B.2个
C.1个
D.0个
A
典题精讲
2 如图,已知AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.3对
C.2对
D.1对
B
探索新知
3
知识点
相似三角形性质的应用
如图所示,要测量一个池塘的
长是多少,不能直接测量的距离,
小明做了△ABC,取池塘的两个点
D,E,使DE∥BC,测出BC,AD,
AB 的长就可以算出DE 的长,你知道为什么吗?
原来由DE∥BC 可以得到△ABC∽△ADE,
所以AD∶AB=DE∶BC
探索新知
归 纳
通过建立相似三角形数学模型可以解决实际问题。
探索新知
如图,在 ABCD 中,AE=EB,AF=2,则FC=________.
例3
4
探索新知
导引:
有平行四边形,就提供了平行线,就有三角形相
似,就有对应边的比相等,就能求出FC 的长.
在 ABCD 中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∴
∵AE=EB,∴
∴FC=2AF=4
探索新知
总 结
求线段的长的方法:对于三角形被平行线所截形成“A”型或“X”型的图形,当所求的线段或已知线段在平行的边上时,通常考虑通过找三角形相似,再利用相似三角形的对应边的比相等构建包含已知与未知线段的比例式,即可求出线段的长;当所求的线段或已知线段不在平行的边上时,则考虑直接用平行线截线段成比例求线段的长.
典题精讲
1 如图,已知AB,CD,EF 都与BD 垂直,垂足分别是B,D,F,且AB=1,CD=3,那么EF 的长是( )
A.
B.
C.
D.
C
典题精讲
2 如图,AB∥CD,AD与BC 相交于点O,那么在下列比例式中,正确的是( )
A.
B.
C.
D.
C
典题精讲
3 如图,在△ABC中,DE∥BC,AE ∶ EC=2 ∶ 3,DE=4,则BC 等于( )
A.10
B.8
C.9
D.6
A
学以致用
小试牛刀
1.在△ABC 中,已知AB=5,BC=4,AC=8.若△ABC∽△A1B1C1,△A1B1C1的最长边的长为16,则其他两边的长分别为( )
A . A1B1=8,B1C1=10
B.A1B1=10,B1C1=8
C.A1B1=5,B1C1=8
D.A1B1=10,B1C1=4
B
小试牛刀
2.已知△ABC∽△A1B1C1,且A1B1=6 cm,AB=4 cm,BC=3.2 cm,∠B=58°,∠C=72°,则B1C1=________cm,∠A1=________°.
4.8
50
3.如果△ABC∽△DEF,且△ABC与△DEF的相似比为k1,△DEF 与△ABC的相似比为k2,则k1与k2的关系是( )
A.k1=k2 B.k1+k2=0
C.k1·k2=-1 D .k1·k2=1
D
小试牛刀
4.如图,在 ABCD 中,M,N 为对角线BD 的三等分点,连接AM 并延长交BC于点E,连接EN并延长交AD于点F.
(1)求证:△AMD∽△EMB;
(2)求 的值.
小试牛刀
(1)证明:∵四边形ABCD 为平行四边形,
∴AD∥BE. ∴△AMD∽△EMB.
(2) ∵AD∥BC,∴△FND∽△ENB.
∴
∵M,N 为BD 的三等分点,∴
∴
小试牛刀
5.如图,在 ABCD 中,点E在边BC 上,点F在边AD 的延长线上,且DF=BE.EF 与CD 交于点G.
(1)求证:BD∥EF;
(2)若 ,BE=4,求EC 的长.
小试牛刀
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵DF=BE,
∴四边形BEFD是平行四边形,
∴BD∥EF.
(2) ∵BE=4,∴DF=4.
∵DF∥EC,
∴△DFG∽△CEG,∴
∴EC=
课堂小结
课堂小结
1.相似三角形的定义具有两种功能:
判定和性质,即对应边成比例、对应角相等 两个三角形相似,注意相似比具有顺序性.
2.平行线截三角形相似的定理:
平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.数学表达式:如图,∵DE∥BC,
∴△ABC∽△ADE.
课堂小结
要点精析:根据定
理得到的相似三角
形的三个基本图形
中都有BC∥DE,图(1)(2)很像大写字母A,故我们称
之为“A”型相似;图(3)很像大写字母X,故我们称之为“X”型相似(也像阿拉伯数字“8”).
3.作用:本定理是相似三角形判定定理的预备定理:它通过平行证三角形相似,再由相似证对应角相等、对应边成比例.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
