冀教版(新)九上-25.5 相似三角形的性质【优质课件】
文档属性
| 名称 | 冀教版(新)九上-25.5 相似三角形的性质【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:39 | ||
图片预览








文档简介
(共47张PPT)
25.5 相似三角形的性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某社区拟筹资金 2000 元,在一块上、下底分别是 10米, 20米的梯形空地上种植花木,他们想在△AMD 和 △BMC 地带种植单价为 10 元/平方米的太阳花,当 △AMD 地带种满花后,已花了500元,请预算一下,若继续在 △BMC 地带种植同样的太阳花,资金是否够用
M
A
D
B
C
20米
新课精讲
问题
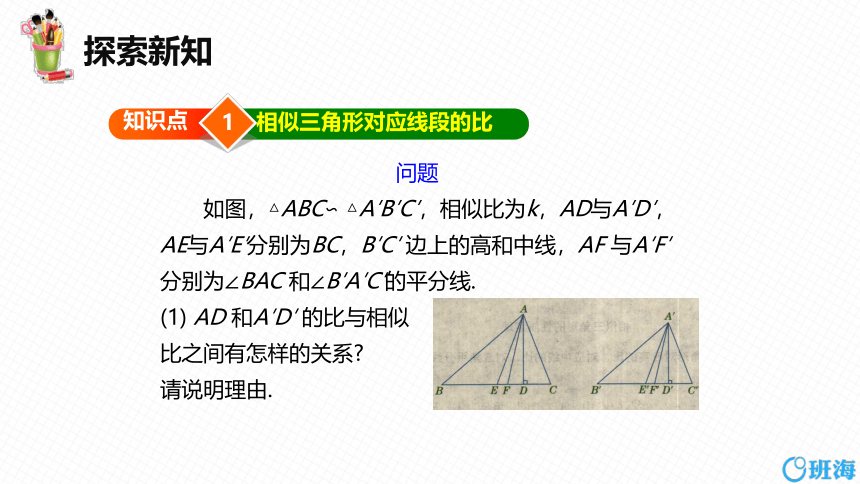
如图,△ABC∽ △A′B′C′,相似比为k,AD与A′D′,AE与A′E′分别为BC,B′C′ 边上的高和中线,AF 与A′F′分别为∠BAC 和∠B′A′C′的平分线.
(1) AD 和A′D′ 的比与相似
比之间有怎样的关系
请说明理由.
探索新知
1
知识点
相似三角形对应线段的比
探索新知
(2)AE 和A′E′ 的比、AF 和A′F′ 的比分别与相似比有怎样的关系 请说明理由.
事实上,两个相似三角形的对应高、对应中线和对
应角平分线的比都等于它们的相似比.
下面,我们证明相似三角形对应高的比等于它们的相似比.
探索新知
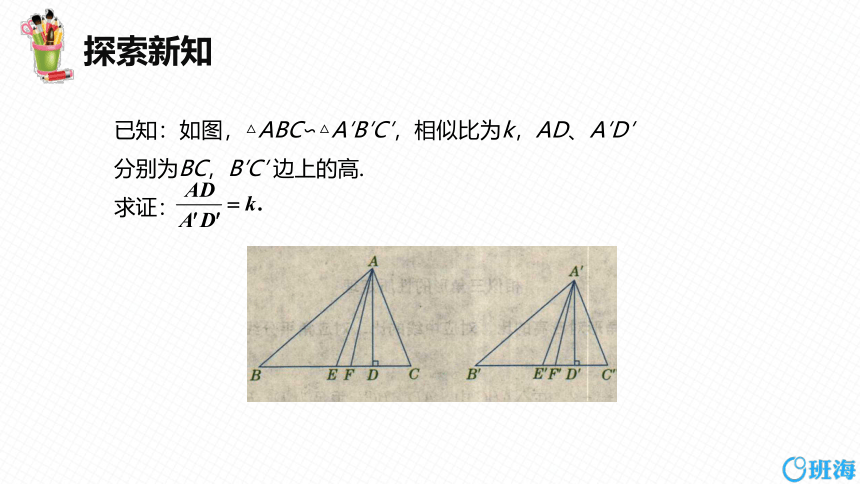
已知:如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′分别为BC,B′C′ 边上的高.
求证:
探索新知
∵△ABC∽△A′B′C′
∴∠B=∠B′.
又∵AD⊥BC, A′D′⊥B′C′,
∴∠ADB=∠A′D′B′=90°.
∴△ABD∽△A′B′D′.
∴
证明:
探索新知
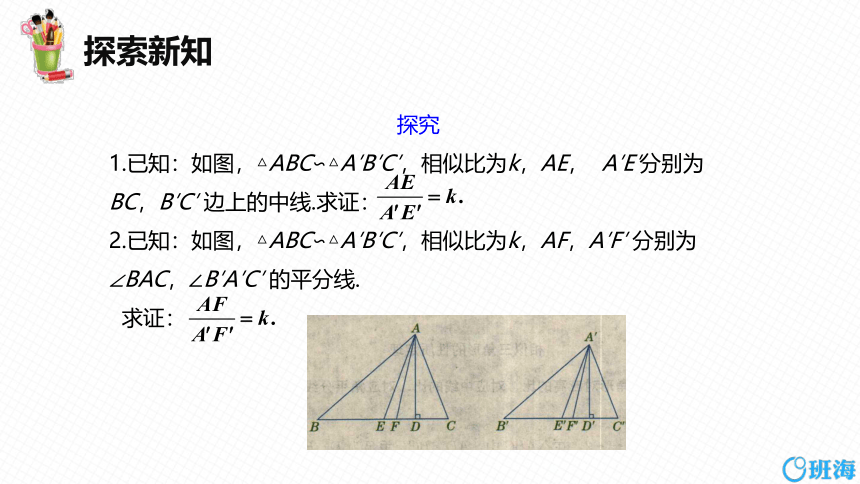
探究
1.已知:如图,△ABC∽△A′B′C′,相似比为k,AE, A′E′分别为BC,B′C′ 边上的中线.求证:
2.已知:如图,△ABC∽△A′B′C′,相似比为k,AF,A′F′ 分别为∠BAC,∠B′A′C′ 的平分线.
求证:
探索新知
总 结
相似三角形的性质定理:
相似三角形对应高的比、对应中线的比、对应角平分线的比,都等于相似比.
探索新知
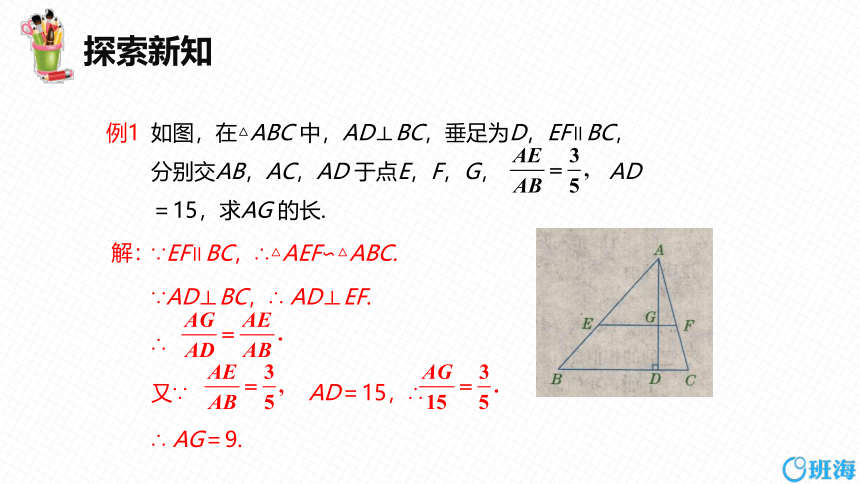
如图,在△ABC 中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD 于点E,F,G, AD=15,求AG 的长.
∵EF∥BC,∴△AEF∽△ABC.
∵AD⊥BC,∴ AD⊥EF.
∴
又∵ AD=15,∴
∴ AG=9.
例1
解:
探索新知
总 结
本题考查了相似三角形的性质,主要利用了相似三角形对应高的比、对应中线的比等于相似比的性质,熟记性质是解题的关键.
典题精讲
1 已知△ABC∽△DEF,若△ABC 与△DEF 的相似比为 ,则△ABC 与△DEF 对应中线的比为( )
A. B. C. D.
A
2 如图,已知△ADE∽△ABC,相似比为2∶5,则AF∶AG 为( )
A.2∶5
B.5∶2
C.5∶1
D.1∶5
A
探索新知
2
知识点
相似三角形周长的比
问题
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米. 现在的问题是:它的周长是多少?
探索新知
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴ 由比例的性质可
解:
将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30m,BD=18m,△ABC
的周长为80m,求△ADE 的周长.
探索新知
又∵△ADE 的周长=AD+AE+DE,
△ABC 的周长=AB+AC+BC,
∴
∴△ADE 的周长=32米.
探索新知
总 结
相似三角形周长的比等于相似比.
探索新知
如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC 的周长之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
例2
A
探索新知
导引:
在Rt△ABC 中,∠A+∠B=90°;
在Rt△BCD 中,∠BCD+∠B=90°,
所以∠BCD=∠A.
又因为∠B=∠B,所以△BCD∽△BAC.
在Rt△ABC 中,∠A=30°,
所以 则△BCD与△ABC 的周长比等于相
似比
探索新知
总 结
相似三角形周长的比等于相似比在解题时,如果是相似图形求周长就常用到周长比等于相似比.
典题精讲
1. △ABC 与△DEF 的相似比为1∶4,则△ABC 与△DEF 的周长比为( )
A.1∶2 B.1∶3
C.1∶4 D.1∶16
C
2. 已知△ABC∽△DEF,相似比为3∶1,且△ABC 的周长为18,则△DEF 的周长为( )
A.2 B.3
C.6 D.54
C
探索新知
3
知识点
相似三角形面积的比
问题
相似三角形面积的比,与它们的相似比之间有什么关系呢?
探索新知
如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′ 分别为BC,B′C′边上的高.
(1)△ABC的面积和△A′B′C′的面积的比与他们的相似比有什么关系 请说明理由.
探索新知
因为
所以
即△ABC与△A′B′C′的面积之比等于相似比的平方.
探索新知
总 结
相似三角形面积的比等于相似比的平方.
探索新知
如图,在△ABC 中,D,E,F分别为BC,AC,AB 边的中点. 求:
(1)△DEF 的周长与△ABC 的周长之比.
(2)△DEF 的面积与△ABC 的面积之比.
例3
探索新知
解:
∵D,E,F分别为BC,AC,AB 的中点,
∴ DE∥AB, EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF 的周长与△ABC 的周长之比为1∶2,
△DEF 的面积与△ABC 的面积之比为1∶4.
探索新知
总 结
利用相似比求周长和面积时,先确定两个三角形相似,然后找准相似比,利用“相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方”解题.
警示: 不要误认为面积的比等于相似比.
典题精讲
1. 如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶16
B.1∶4
C.1∶6
D.1∶2
D
典题精讲
2. 如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为( )
A.15
B.10
C.
D.5
D
学以致用
小试牛刀
1.已知△ABC∽△DEF,若△ABC 与△DEF 的相似比为 ,则△ABC与△DEF 对应中线的比为( )
A. B. C. D.
2.已知△ABC∽△A′B ′C ′,BD 和B ′D ′分别是两个三角形对应角的平分线,且AC∶A′C ′=2∶3,若BD=4 cm,则B ′D ′的长是( )
A.3 cm B.4 cm C.6 cm D.8 cm
A
C
小试牛刀
3.若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5
C.9∶4 D.4∶9
A
4.△ABC 与△DEF 的相似比为1∶4,则△ABC 与△DEF 的周长比为( )
A.1∶2 B.1∶3
C.1∶4 D.1∶16
C
小试牛刀
5.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1:2
B.1:3
C.1:4
D.1:5
A
小试牛刀
6. 判断题(正确的画“√”,错误的画“×”).
(1) 一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )
√
×
小试牛刀
7.有3个正方形按如图所示放置,阴影部分的面积依次记为S1,S2,则S1: S2等于( )
A.1:
B.1:2
C.2:3
D.4:9
D
小试牛刀
8.如图,四边形ABCD 为菱形,M 为BC上一点,连接AM 交对角线BD 于点G,并且∠ABC=2∠BAM.
(1)求证:AG=BG;
(2)若M为BC的中点,同时S△BGM=1,求三角形ADG
的面积.
小试牛刀
∵四边形ABCD为菱形,
∴BD平分∠ABC.
∴∠ABC=2∠ABG.
又∵∠ABC=2∠BAM,
∴∠BAG=∠ABG.
∴AG=BG.
证明:
(1)求证:AG=BG;
小试牛刀
证明:
(2)若M 为BC 的中点,同时S△BGM=1,求三角形ADG 的面积.
∵四边形ABCD为菱形,
∴AD∥BC,AD=BC.
∴△BGM∽△DGA.
∵M为BC的中点,∴BM= BC= AD.
即△BGM与△DGA的相似比为1∶2,
∴S△BGM∶S△DGA=1∶4.
∵S△BGM=1,∴S△DGA=4.
小试牛刀
9.如图,有一批呈直角三角形,大小相同的不锈钢片,已知∠C=90°,AC=12 cm,BC=5 cm,要用这批不锈钢片裁出面积最大的正方形不锈钢片,请设计一种方案,并求出这种正方形不锈钢片的边长.
小试牛刀
解:
如图①,设正方形EFGH 的边长为x cm,过点C 作CD
⊥AB 于点D,交EH 于点M.易知CM⊥EH.
因为∠ACB=90°,AC=12 cm,BC=5 cm,
所以AB= =13(cm).
又因为AB·CD=AC·BC,
所以CD= (cm).
又因为EH∥AB,所以△CEH∽△CAB.
小试牛刀
所以
如图②,设正方形CEGH 的边长为y cm.
因为GH∥AC,所以= 即
解得y=
因为
所以应按图②裁剪,这时正方形不锈钢片的面积最大,
它的边长为 cm.
课堂小结
课堂小结
课堂总结 知识方法要点 关键总结 注意事项
相似三角形的对应高、对应中线、对应角平分线的比的性质 相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比; 注意相似比是有顺序的
相似三角形的周长和面积比的性质 相似三角形的周长比等于相似比,面积比等于相似比的平方 不要误认为面积比等于相似比,更不要根据面积求相似比时,不开方反而平方
课堂小结
方法规律总结:
当相似三角形的问题中出现高、中线或角平分线时,要考虑用相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比;当相似三角形中出现周长或面积时,要考虑用相似三角形的周长比等于相似比,面积比等于相似比的平方;相似多边形也有周长比等于相似比,面积比等于相似比的平方的性质,以后也可以直接利用
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.5 相似三角形的性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某社区拟筹资金 2000 元,在一块上、下底分别是 10米, 20米的梯形空地上种植花木,他们想在△AMD 和 △BMC 地带种植单价为 10 元/平方米的太阳花,当 △AMD 地带种满花后,已花了500元,请预算一下,若继续在 △BMC 地带种植同样的太阳花,资金是否够用
M
A
D
B
C
20米
新课精讲
问题
如图,△ABC∽ △A′B′C′,相似比为k,AD与A′D′,AE与A′E′分别为BC,B′C′ 边上的高和中线,AF 与A′F′分别为∠BAC 和∠B′A′C′的平分线.
(1) AD 和A′D′ 的比与相似
比之间有怎样的关系
请说明理由.
探索新知
1
知识点
相似三角形对应线段的比
探索新知
(2)AE 和A′E′ 的比、AF 和A′F′ 的比分别与相似比有怎样的关系 请说明理由.
事实上,两个相似三角形的对应高、对应中线和对
应角平分线的比都等于它们的相似比.
下面,我们证明相似三角形对应高的比等于它们的相似比.
探索新知
已知:如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′分别为BC,B′C′ 边上的高.
求证:
探索新知
∵△ABC∽△A′B′C′
∴∠B=∠B′.
又∵AD⊥BC, A′D′⊥B′C′,
∴∠ADB=∠A′D′B′=90°.
∴△ABD∽△A′B′D′.
∴
证明:
探索新知
探究
1.已知:如图,△ABC∽△A′B′C′,相似比为k,AE, A′E′分别为BC,B′C′ 边上的中线.求证:
2.已知:如图,△ABC∽△A′B′C′,相似比为k,AF,A′F′ 分别为∠BAC,∠B′A′C′ 的平分线.
求证:
探索新知
总 结
相似三角形的性质定理:
相似三角形对应高的比、对应中线的比、对应角平分线的比,都等于相似比.
探索新知
如图,在△ABC 中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD 于点E,F,G, AD=15,求AG 的长.
∵EF∥BC,∴△AEF∽△ABC.
∵AD⊥BC,∴ AD⊥EF.
∴
又∵ AD=15,∴
∴ AG=9.
例1
解:
探索新知
总 结
本题考查了相似三角形的性质,主要利用了相似三角形对应高的比、对应中线的比等于相似比的性质,熟记性质是解题的关键.
典题精讲
1 已知△ABC∽△DEF,若△ABC 与△DEF 的相似比为 ,则△ABC 与△DEF 对应中线的比为( )
A. B. C. D.
A
2 如图,已知△ADE∽△ABC,相似比为2∶5,则AF∶AG 为( )
A.2∶5
B.5∶2
C.5∶1
D.1∶5
A
探索新知
2
知识点
相似三角形周长的比
问题
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米. 现在的问题是:它的周长是多少?
探索新知
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴ 由比例的性质可
解:
将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30m,BD=18m,△ABC
的周长为80m,求△ADE 的周长.
探索新知
又∵△ADE 的周长=AD+AE+DE,
△ABC 的周长=AB+AC+BC,
∴
∴△ADE 的周长=32米.
探索新知
总 结
相似三角形周长的比等于相似比.
探索新知
如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC 的周长之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
例2
A
探索新知
导引:
在Rt△ABC 中,∠A+∠B=90°;
在Rt△BCD 中,∠BCD+∠B=90°,
所以∠BCD=∠A.
又因为∠B=∠B,所以△BCD∽△BAC.
在Rt△ABC 中,∠A=30°,
所以 则△BCD与△ABC 的周长比等于相
似比
探索新知
总 结
相似三角形周长的比等于相似比在解题时,如果是相似图形求周长就常用到周长比等于相似比.
典题精讲
1. △ABC 与△DEF 的相似比为1∶4,则△ABC 与△DEF 的周长比为( )
A.1∶2 B.1∶3
C.1∶4 D.1∶16
C
2. 已知△ABC∽△DEF,相似比为3∶1,且△ABC 的周长为18,则△DEF 的周长为( )
A.2 B.3
C.6 D.54
C
探索新知
3
知识点
相似三角形面积的比
问题
相似三角形面积的比,与它们的相似比之间有什么关系呢?
探索新知
如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′ 分别为BC,B′C′边上的高.
(1)△ABC的面积和△A′B′C′的面积的比与他们的相似比有什么关系 请说明理由.
探索新知
因为
所以
即△ABC与△A′B′C′的面积之比等于相似比的平方.
探索新知
总 结
相似三角形面积的比等于相似比的平方.
探索新知
如图,在△ABC 中,D,E,F分别为BC,AC,AB 边的中点. 求:
(1)△DEF 的周长与△ABC 的周长之比.
(2)△DEF 的面积与△ABC 的面积之比.
例3
探索新知
解:
∵D,E,F分别为BC,AC,AB 的中点,
∴ DE∥AB, EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF 的周长与△ABC 的周长之比为1∶2,
△DEF 的面积与△ABC 的面积之比为1∶4.
探索新知
总 结
利用相似比求周长和面积时,先确定两个三角形相似,然后找准相似比,利用“相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方”解题.
警示: 不要误认为面积的比等于相似比.
典题精讲
1. 如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶16
B.1∶4
C.1∶6
D.1∶2
D
典题精讲
2. 如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为( )
A.15
B.10
C.
D.5
D
学以致用
小试牛刀
1.已知△ABC∽△DEF,若△ABC 与△DEF 的相似比为 ,则△ABC与△DEF 对应中线的比为( )
A. B. C. D.
2.已知△ABC∽△A′B ′C ′,BD 和B ′D ′分别是两个三角形对应角的平分线,且AC∶A′C ′=2∶3,若BD=4 cm,则B ′D ′的长是( )
A.3 cm B.4 cm C.6 cm D.8 cm
A
C
小试牛刀
3.若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5
C.9∶4 D.4∶9
A
4.△ABC 与△DEF 的相似比为1∶4,则△ABC 与△DEF 的周长比为( )
A.1∶2 B.1∶3
C.1∶4 D.1∶16
C
小试牛刀
5.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1:2
B.1:3
C.1:4
D.1:5
A
小试牛刀
6. 判断题(正确的画“√”,错误的画“×”).
(1) 一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )
√
×
小试牛刀
7.有3个正方形按如图所示放置,阴影部分的面积依次记为S1,S2,则S1: S2等于( )
A.1:
B.1:2
C.2:3
D.4:9
D
小试牛刀
8.如图,四边形ABCD 为菱形,M 为BC上一点,连接AM 交对角线BD 于点G,并且∠ABC=2∠BAM.
(1)求证:AG=BG;
(2)若M为BC的中点,同时S△BGM=1,求三角形ADG
的面积.
小试牛刀
∵四边形ABCD为菱形,
∴BD平分∠ABC.
∴∠ABC=2∠ABG.
又∵∠ABC=2∠BAM,
∴∠BAG=∠ABG.
∴AG=BG.
证明:
(1)求证:AG=BG;
小试牛刀
证明:
(2)若M 为BC 的中点,同时S△BGM=1,求三角形ADG 的面积.
∵四边形ABCD为菱形,
∴AD∥BC,AD=BC.
∴△BGM∽△DGA.
∵M为BC的中点,∴BM= BC= AD.
即△BGM与△DGA的相似比为1∶2,
∴S△BGM∶S△DGA=1∶4.
∵S△BGM=1,∴S△DGA=4.
小试牛刀
9.如图,有一批呈直角三角形,大小相同的不锈钢片,已知∠C=90°,AC=12 cm,BC=5 cm,要用这批不锈钢片裁出面积最大的正方形不锈钢片,请设计一种方案,并求出这种正方形不锈钢片的边长.
小试牛刀
解:
如图①,设正方形EFGH 的边长为x cm,过点C 作CD
⊥AB 于点D,交EH 于点M.易知CM⊥EH.
因为∠ACB=90°,AC=12 cm,BC=5 cm,
所以AB= =13(cm).
又因为AB·CD=AC·BC,
所以CD= (cm).
又因为EH∥AB,所以△CEH∽△CAB.
小试牛刀
所以
如图②,设正方形CEGH 的边长为y cm.
因为GH∥AC,所以= 即
解得y=
因为
所以应按图②裁剪,这时正方形不锈钢片的面积最大,
它的边长为 cm.
课堂小结
课堂小结
课堂总结 知识方法要点 关键总结 注意事项
相似三角形的对应高、对应中线、对应角平分线的比的性质 相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比; 注意相似比是有顺序的
相似三角形的周长和面积比的性质 相似三角形的周长比等于相似比,面积比等于相似比的平方 不要误认为面积比等于相似比,更不要根据面积求相似比时,不开方反而平方
课堂小结
方法规律总结:
当相似三角形的问题中出现高、中线或角平分线时,要考虑用相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比;当相似三角形中出现周长或面积时,要考虑用相似三角形的周长比等于相似比,面积比等于相似比的平方;相似多边形也有周长比等于相似比,面积比等于相似比的平方的性质,以后也可以直接利用
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
