冀教版(新)九上-25.6 相似三角形的应用【优质课件】
文档属性
| 名称 | 冀教版(新)九上-25.6 相似三角形的应用【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
25.6 相似三角形的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
埃及金字塔到底有多高 据史料记载:古希腊科学家泰勒斯利用相似三角形的原理,借助金字塔在太阳光线下形成的影子测出了金字塔的高度.你知道他是怎样测量的吗 今天我们就利用这些知识测量一些不能直接测量的物体的高度吧!
新课精讲
探索新知
1
知识点
利用光照下的影子
对于学校里旗杆的高度,我们是无法直接进行测量的.但是我们可以根据相似三角形的知识,测出旗杆的高度.结合下面图形大家思考如何求出高度?
探索新知
利用阳光下的影子测高:
(1)构造相似三角形,如图,
(2)测量数据:AB (身高),BC (人影长),BE (旗杆影长);
待求数据:DE (旗杆高).
(3)计算理由:因为AC∥DB(平行光),所以∠ACB=∠DBE.
因为∠ABC=∠DEB=90°(直立即为垂直),
所以△ABC∽△DEB,有
探索新知
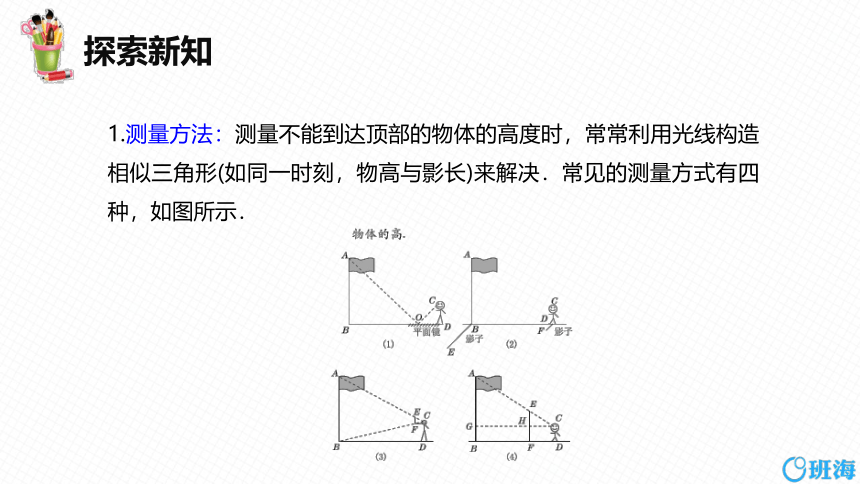
1.测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.
探索新知
2.要点精析:
(1)由于太阳在不停地移动,影子的长也随着太阳的移动而发生变化.因此,测量影子的长一定要在同一时刻下进行,否则就会影响结果的准确性.
(2)太阳离我们非常远,因此可以把太阳光线近似地看成平行光线.
(3)此方法要求被测物体的底部可以到达,否则测不到被测物体的影长,从而计算不出物体的高.
探索新知
如何测量旗杆的高度,说明具体过程及原理.
具体过程:
(1)依据.同一时刻,物体的高度与其影长成比例.
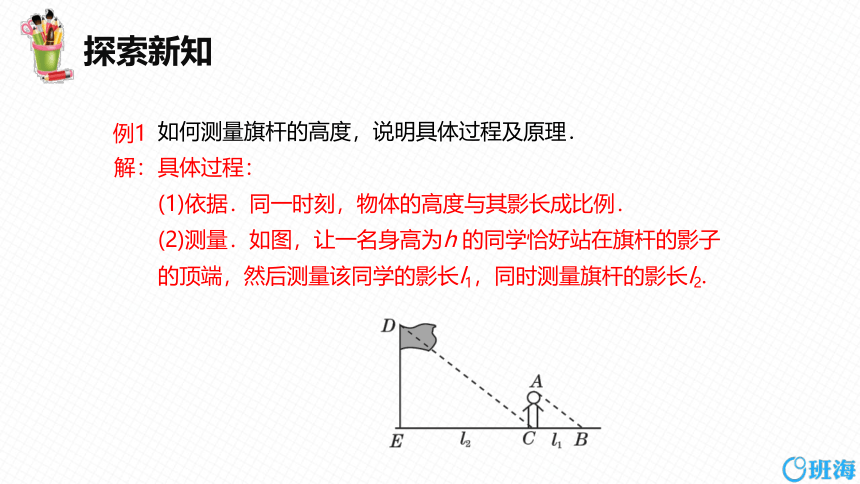
(2)测量.如图,让一名身高为h 的同学恰好站在旗杆的影子的顶端,然后测量该同学的影长l1,同时测量旗杆的影长l2.
例1
解:
探索新知
(3)计算.
∵太阳光线是平行光线,∴AB∥CD,
∴∠ABC=∠DCE.
∵∠ACB=∠DEC=90°,
∴△ACB∽△DEC,
∵AC=h,BC=l1,EC=l2,
探索新知
总 结
利用影长测量不能直接测量的物高(可到底部)的方法:
利用同一时刻的太阳光线构造两个相似三角形,利用相似三角形对应边的比相等列出关于物高、物影、人高、人影的比例关系式,然后通过测量物影、人高、人影来计算出物高.
典题精讲
1 如图,身高为1.6m的某学生想测量学校旗杆的高度,当他站在C 处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )
A.6.4m
B.7.0m
C.8.0m
D.9.0m
探索新知
2
知识点
利用工具
问题
小明想利用树影测量树高,他
在某一时刻测得长为1m的竹竿影长
0.9m,但当他马上测量树影时,因
树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如下图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少
探索新知
过点C 作CE⊥AB 于点E,因此BE=CD=1.2m,CE=
BD=2.7 m,由 可得AE=3 m,所以AB=AE+BE=1.2+3=4.2 m.
这棵树的高度为4.2 m.
分析:
答案:
探索新知
1.与测量有关的概念:
(1)视点:观察物体时人的眼睛称为视点.
(2)仰角:测量物体的高度时,水平视线与观察物体的视线间的夹称为仰角.
(3)盲区:人的视线看不到的区域称为盲区.
2.测量原理:用标杆和直尺作为三角形的边,利用视点和盲区的知识构造相似三角形.
探索新知
3.测量方法:如图,观察者的眼睛C必
须与标杆的顶端 D 和物体的顶端 A
“三点共线”,标杆与地面要垂直,
测量出标杆的高度DF,人眼离地面的高度CE,人与标杆的距离EF,标杆与物体的距FG,利用相似三角形“对应边的比相等” 的性质求物体的高度AG.
要点精析:利用标杆测量物体的高度也叫目测,在日常生活中有着广泛的应用,必要时可 以用自己的身高和臂长等作为测量工具.
探索新知
如图,左、右并排的两棵大树的高分别为AB=8m和CD=12 m,两树底部的距离BD=5 m,一个人估计自己眼睛距地面1.6 m. 她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了
例2
探索新知
分析:
如图 (1),设观察者眼睛的位置为点F,画出观察者的水平视线FG,分别交AB, CD于点H,K.视线FA与FG的夹角∠AFH是观察点A时的仰角.类似地,∠CFK是观察点C时的仰角.由于树的遮挡, 区域I和II,观察者都看不到.
如图(2),假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树的顶端A,C恰在一条直线上.
解:
探索新知
∵AB⊥l,CD ⊥l,∴AB∥CD.
∴△AEH∽△CEK.
∴ 即
解得 EH=8m.
由此可知,如果观察者继续前进,当她与左边的树的距离小于8 m时,由 于这棵树的遮挡,她看不到右边树的顶端C.
探索新知
总 结
测量高度和距离时,往往需要建立几何模型构造相似三角形,利用相似三角形的性质直接求解或列方程求解.
典题精讲
1.为了测量校园水平地面土一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索,根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案,把一面很小的镜子水平放置在离树(B)8.4m的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2m,观察者目高CD=1.6m,则树(AB)的高度为( )
A.4.2m B.4.8m C.6.4m D.16.8m
A
典题精讲
2.如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则楼高CD为____________.
12m
探索新知
3
知识点
利用镜子反射
问题
若在一个阴天,没有太阳光,还能测量金字塔的高度吗
探索新知
用镜面反射(如下图,点A是个小镜子,根据光的反射定律:由入射角等于反射角构造相似三角形).
根据光的反射定律由入射角等于反射角构造△AOB
与△AFE 相似,即可利用对应边的比相等求出BO.
分析:
探索新知
利用相似三角形测量的一般步骤:
利用相似三角形的知识对未知量(高度、宽度等)进行测
量,一般要经历以下几个步骤:
(1)利用平行线、标杆等构造相似三角形;
(2)测量与表示未知量的线段相对应的边长以及另外任意一组对应边的长度;
(3)画出示意图,利用相似三角形的性质,列出以上包括未知量在内的四个量的比例式,解出未知量;
(4)检验并得出答案.
探索新知
如图所示,小丽为了测量高楼MN 的高度,在离N点20m的A处放了一个平面镜,小丽沿NA方向向后退到C点,正好从镜中看到楼顶M点.若AC 等于1.5m,小丽的眼睛离地面的高度BC 为1.6m,请你帮助小丽计算一下此楼的高度(精确到0.1m).
例3
导引:
根据反射角等于入射角,得到
△BCA与△MNA相似,列出比
例式,问题即可解决.
探索新知
解:
如图,过点A作OA⊥CN,
∵BC⊥CA,MN⊥NA,
∴∠BCA=∠MNA=90°.
又∵∠BAO=∠MAO,
∴∠BAC=∠MAN.∴△BCA∽△MNA.
∴MN≈21.3m.
即此楼的高度约为21.3m.
探索新知
总 结
测量不能直接到达的两点间的距离,关键是构造两个相似三角形,利用能测量的三角形的边长及相似三角形的性质求此距离.
典题精讲
1.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P 处放一水平的平面镜,光线从点A发出经平面镜反射后刚好到古城墙CD 的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2m,BP=3m,PD=12m,那么该古城墙的高度CD是________.
8m
学以致用
小试牛刀
1.小虎的身高为1.6米,他的影长为2米,同一时刻他测得电线杆的影长为18米,则此电线杆的高度为( )
A.20米
B.14.4米
C.16.4米
D.15.4米
B
小试牛刀
2.为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
A.21m B.24m C.27m D.8.6m
C
小试牛刀
3.一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
C
小试牛刀
4.已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外,将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为____________.
7.5m
小试牛刀
5.如图,一条河的两岸有一段平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为__________米.
22.5m
小试牛刀
6.如图,AB是⊙O的直径,点P 在BA 的延长线上,弦CD⊥AB,垂足为E,且PC 2=PE·PO.
(1)求证:PC 是⊙O 的切线.
(2)若OE∶EA=1∶2,PA=6,
求⊙O 的半径.
小试牛刀
证明:
(1)求证:PC 是⊙O 的切线.
连接OC,如图,
∵CD⊥AB,∴∠PEC=90°,
∵PC 2=PE·PO,
∴PC∶PO=PE∶PC,
而∠CPE=∠OPC,
∴△PCE∽△POC.
∴∠PCO=∠PEC=90°.∴OC⊥PC.
∴PC 是⊙O 的切线.
小试牛刀
设OE=x,则EA=2x,OA=OC=3x.
∵∠COE=∠POC,∠OEC=∠OCP,
∴△OCE∽△OPC.
∴OC∶OP=OE∶OC,即3x∶OP=x∶3x,
解得OP=9x.
∵OA+AP=OP,
∴3x+6=9x,解得x=1.
∴OC=3.即⊙O 的半径为3.
(2)若OE∶EA=1∶2,PA=6,求⊙O 的半径.
解:
小试牛刀
7.已知:如图,MN 为⊙O 的直径,ME 是⊙O 的弦,MD垂直于过点E的直线DE,垂足为点D,且ME 平分∠DMN.
求证:(1)DE 是⊙O 的切线;
(2)ME 2=MD ·MN.
小试牛刀
证明:
∵ME 平分∠DMN,∴∠OME=∠DME.
∵OM=OE,∴∠OME=∠OEM.
∴∠DME=∠OEM.∴OE∥MD.
∵MD⊥DE,∴OE⊥DE.
又∵OE 是⊙O 的半径,
∴DE 是⊙O 的切线.
(1)DE 是⊙O 的切线;
小试牛刀
证明:
(2)ME 2=MD ·MN.
如图,连接EN.
∵DM⊥DE,MN 为⊙O 的直径,
∴∠MDE=∠MEN=90°.
∵∠DME=∠NME,
∴△MDE∽△MEN.
∴
∴ME 2=MD MN.
课堂小结
课堂小结
知识总结 知识方法要点 关键总结 注意事项
利用相似三角形测高 根据 利用阳光下的影子测高 测量要尽量减少误差,取每种方法计算出的高度的平均 值,可使误差降到最小
方法规律总结 用相似三角形知识解决实际问题时的方法: ① 将实际问题转化为相似三角形问题; ② 构造出一对相似三角形; ③ 根据相似三角形的性质,建立比例式,求出相应的量 同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.6 相似三角形的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
埃及金字塔到底有多高 据史料记载:古希腊科学家泰勒斯利用相似三角形的原理,借助金字塔在太阳光线下形成的影子测出了金字塔的高度.你知道他是怎样测量的吗 今天我们就利用这些知识测量一些不能直接测量的物体的高度吧!
新课精讲
探索新知
1
知识点
利用光照下的影子
对于学校里旗杆的高度,我们是无法直接进行测量的.但是我们可以根据相似三角形的知识,测出旗杆的高度.结合下面图形大家思考如何求出高度?
探索新知
利用阳光下的影子测高:
(1)构造相似三角形,如图,
(2)测量数据:AB (身高),BC (人影长),BE (旗杆影长);
待求数据:DE (旗杆高).
(3)计算理由:因为AC∥DB(平行光),所以∠ACB=∠DBE.
因为∠ABC=∠DEB=90°(直立即为垂直),
所以△ABC∽△DEB,有
探索新知
1.测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.
探索新知
2.要点精析:
(1)由于太阳在不停地移动,影子的长也随着太阳的移动而发生变化.因此,测量影子的长一定要在同一时刻下进行,否则就会影响结果的准确性.
(2)太阳离我们非常远,因此可以把太阳光线近似地看成平行光线.
(3)此方法要求被测物体的底部可以到达,否则测不到被测物体的影长,从而计算不出物体的高.
探索新知
如何测量旗杆的高度,说明具体过程及原理.
具体过程:
(1)依据.同一时刻,物体的高度与其影长成比例.
(2)测量.如图,让一名身高为h 的同学恰好站在旗杆的影子的顶端,然后测量该同学的影长l1,同时测量旗杆的影长l2.
例1
解:
探索新知
(3)计算.
∵太阳光线是平行光线,∴AB∥CD,
∴∠ABC=∠DCE.
∵∠ACB=∠DEC=90°,
∴△ACB∽△DEC,
∵AC=h,BC=l1,EC=l2,
探索新知
总 结
利用影长测量不能直接测量的物高(可到底部)的方法:
利用同一时刻的太阳光线构造两个相似三角形,利用相似三角形对应边的比相等列出关于物高、物影、人高、人影的比例关系式,然后通过测量物影、人高、人影来计算出物高.
典题精讲
1 如图,身高为1.6m的某学生想测量学校旗杆的高度,当他站在C 处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )
A.6.4m
B.7.0m
C.8.0m
D.9.0m
探索新知
2
知识点
利用工具
问题
小明想利用树影测量树高,他
在某一时刻测得长为1m的竹竿影长
0.9m,但当他马上测量树影时,因
树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如下图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少
探索新知
过点C 作CE⊥AB 于点E,因此BE=CD=1.2m,CE=
BD=2.7 m,由 可得AE=3 m,所以AB=AE+BE=1.2+3=4.2 m.
这棵树的高度为4.2 m.
分析:
答案:
探索新知
1.与测量有关的概念:
(1)视点:观察物体时人的眼睛称为视点.
(2)仰角:测量物体的高度时,水平视线与观察物体的视线间的夹称为仰角.
(3)盲区:人的视线看不到的区域称为盲区.
2.测量原理:用标杆和直尺作为三角形的边,利用视点和盲区的知识构造相似三角形.
探索新知
3.测量方法:如图,观察者的眼睛C必
须与标杆的顶端 D 和物体的顶端 A
“三点共线”,标杆与地面要垂直,
测量出标杆的高度DF,人眼离地面的高度CE,人与标杆的距离EF,标杆与物体的距FG,利用相似三角形“对应边的比相等” 的性质求物体的高度AG.
要点精析:利用标杆测量物体的高度也叫目测,在日常生活中有着广泛的应用,必要时可 以用自己的身高和臂长等作为测量工具.
探索新知
如图,左、右并排的两棵大树的高分别为AB=8m和CD=12 m,两树底部的距离BD=5 m,一个人估计自己眼睛距地面1.6 m. 她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了
例2
探索新知
分析:
如图 (1),设观察者眼睛的位置为点F,画出观察者的水平视线FG,分别交AB, CD于点H,K.视线FA与FG的夹角∠AFH是观察点A时的仰角.类似地,∠CFK是观察点C时的仰角.由于树的遮挡, 区域I和II,观察者都看不到.
如图(2),假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树的顶端A,C恰在一条直线上.
解:
探索新知
∵AB⊥l,CD ⊥l,∴AB∥CD.
∴△AEH∽△CEK.
∴ 即
解得 EH=8m.
由此可知,如果观察者继续前进,当她与左边的树的距离小于8 m时,由 于这棵树的遮挡,她看不到右边树的顶端C.
探索新知
总 结
测量高度和距离时,往往需要建立几何模型构造相似三角形,利用相似三角形的性质直接求解或列方程求解.
典题精讲
1.为了测量校园水平地面土一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索,根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案,把一面很小的镜子水平放置在离树(B)8.4m的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2m,观察者目高CD=1.6m,则树(AB)的高度为( )
A.4.2m B.4.8m C.6.4m D.16.8m
A
典题精讲
2.如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则楼高CD为____________.
12m
探索新知
3
知识点
利用镜子反射
问题
若在一个阴天,没有太阳光,还能测量金字塔的高度吗
探索新知
用镜面反射(如下图,点A是个小镜子,根据光的反射定律:由入射角等于反射角构造相似三角形).
根据光的反射定律由入射角等于反射角构造△AOB
与△AFE 相似,即可利用对应边的比相等求出BO.
分析:
探索新知
利用相似三角形测量的一般步骤:
利用相似三角形的知识对未知量(高度、宽度等)进行测
量,一般要经历以下几个步骤:
(1)利用平行线、标杆等构造相似三角形;
(2)测量与表示未知量的线段相对应的边长以及另外任意一组对应边的长度;
(3)画出示意图,利用相似三角形的性质,列出以上包括未知量在内的四个量的比例式,解出未知量;
(4)检验并得出答案.
探索新知
如图所示,小丽为了测量高楼MN 的高度,在离N点20m的A处放了一个平面镜,小丽沿NA方向向后退到C点,正好从镜中看到楼顶M点.若AC 等于1.5m,小丽的眼睛离地面的高度BC 为1.6m,请你帮助小丽计算一下此楼的高度(精确到0.1m).
例3
导引:
根据反射角等于入射角,得到
△BCA与△MNA相似,列出比
例式,问题即可解决.
探索新知
解:
如图,过点A作OA⊥CN,
∵BC⊥CA,MN⊥NA,
∴∠BCA=∠MNA=90°.
又∵∠BAO=∠MAO,
∴∠BAC=∠MAN.∴△BCA∽△MNA.
∴MN≈21.3m.
即此楼的高度约为21.3m.
探索新知
总 结
测量不能直接到达的两点间的距离,关键是构造两个相似三角形,利用能测量的三角形的边长及相似三角形的性质求此距离.
典题精讲
1.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P 处放一水平的平面镜,光线从点A发出经平面镜反射后刚好到古城墙CD 的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2m,BP=3m,PD=12m,那么该古城墙的高度CD是________.
8m
学以致用
小试牛刀
1.小虎的身高为1.6米,他的影长为2米,同一时刻他测得电线杆的影长为18米,则此电线杆的高度为( )
A.20米
B.14.4米
C.16.4米
D.15.4米
B
小试牛刀
2.为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
A.21m B.24m C.27m D.8.6m
C
小试牛刀
3.一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
C
小试牛刀
4.已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外,将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为____________.
7.5m
小试牛刀
5.如图,一条河的两岸有一段平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为__________米.
22.5m
小试牛刀
6.如图,AB是⊙O的直径,点P 在BA 的延长线上,弦CD⊥AB,垂足为E,且PC 2=PE·PO.
(1)求证:PC 是⊙O 的切线.
(2)若OE∶EA=1∶2,PA=6,
求⊙O 的半径.
小试牛刀
证明:
(1)求证:PC 是⊙O 的切线.
连接OC,如图,
∵CD⊥AB,∴∠PEC=90°,
∵PC 2=PE·PO,
∴PC∶PO=PE∶PC,
而∠CPE=∠OPC,
∴△PCE∽△POC.
∴∠PCO=∠PEC=90°.∴OC⊥PC.
∴PC 是⊙O 的切线.
小试牛刀
设OE=x,则EA=2x,OA=OC=3x.
∵∠COE=∠POC,∠OEC=∠OCP,
∴△OCE∽△OPC.
∴OC∶OP=OE∶OC,即3x∶OP=x∶3x,
解得OP=9x.
∵OA+AP=OP,
∴3x+6=9x,解得x=1.
∴OC=3.即⊙O 的半径为3.
(2)若OE∶EA=1∶2,PA=6,求⊙O 的半径.
解:
小试牛刀
7.已知:如图,MN 为⊙O 的直径,ME 是⊙O 的弦,MD垂直于过点E的直线DE,垂足为点D,且ME 平分∠DMN.
求证:(1)DE 是⊙O 的切线;
(2)ME 2=MD ·MN.
小试牛刀
证明:
∵ME 平分∠DMN,∴∠OME=∠DME.
∵OM=OE,∴∠OME=∠OEM.
∴∠DME=∠OEM.∴OE∥MD.
∵MD⊥DE,∴OE⊥DE.
又∵OE 是⊙O 的半径,
∴DE 是⊙O 的切线.
(1)DE 是⊙O 的切线;
小试牛刀
证明:
(2)ME 2=MD ·MN.
如图,连接EN.
∵DM⊥DE,MN 为⊙O 的直径,
∴∠MDE=∠MEN=90°.
∵∠DME=∠NME,
∴△MDE∽△MEN.
∴
∴ME 2=MD MN.
课堂小结
课堂小结
知识总结 知识方法要点 关键总结 注意事项
利用相似三角形测高 根据 利用阳光下的影子测高 测量要尽量减少误差,取每种方法计算出的高度的平均 值,可使误差降到最小
方法规律总结 用相似三角形知识解决实际问题时的方法: ① 将实际问题转化为相似三角形问题; ② 构造出一对相似三角形; ③ 根据相似三角形的性质,建立比例式,求出相应的量 同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
