冀教版(新)九上-25.7 相似多边形和图形的位似 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-25.7 相似多边形和图形的位似 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:39 | ||
图片预览










文档简介
(共39张PPT)
25.7 相似多边形和图形的位似
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
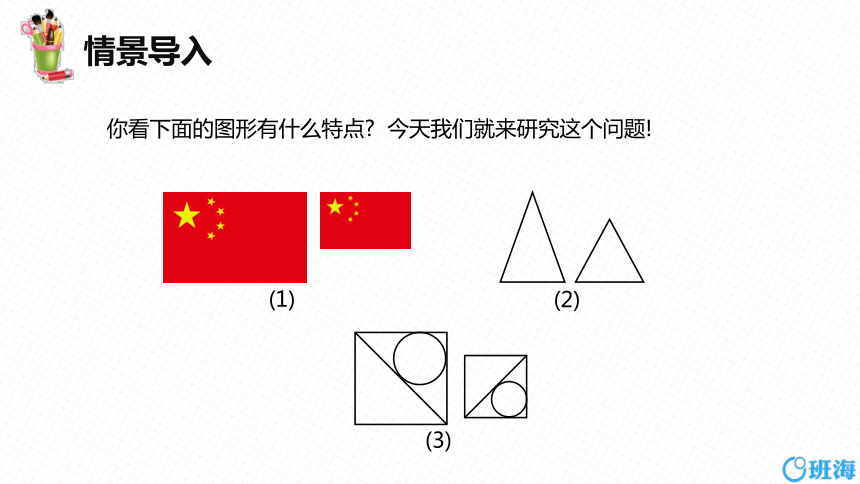
情景导入
你看下面的图形有什么特点 今天我们就来研究这个问题!
(1)
(2)
(3)
新课精讲
探索新知
1
知识点
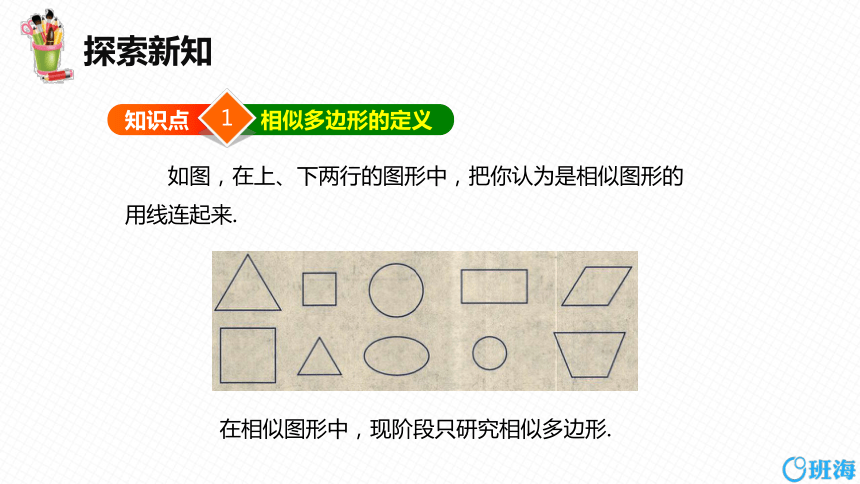
相似多边形的定义
如图,在上、下两行的图形中,把你认为是相似图形的用线连起来.
在相似图形中,现阶段只研究相似多边形.
探索新知
归 纳
一般地,如果两个多边形的对应角相等、对应边成比例,那么这两个多边形就叫做相似多边形(similar polygons).
探索新知
1.定义:形状相同的图形叫做相似图形.
要点精析:
(1) “形状相同”是判定相似图形的唯一条件.
(2)相似图形之间的关系:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
(3)相似与全等的关系:当两个图形的形状相同、大小也相同时,它们是全等图形,全等图形是相似图形的特殊情况,即全等图形一定是相似图形,但相似图形不一定是全等图形,只有相似图形的大小相同时,它们才全等.
探索新知
2.易错警示:
(1)两个图形相似是指它们的形状相同,与它们的位置、大小无关;
(2)全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
探索新知
下图中的相似图形有哪些
例1
导引:
本题依据相似图形的定义求解.观察这些图形,虽然图(6)与图(12)、图(8)与图(11)极为相似,但是它们的形状不相同.图(6)“拉长”而不是整体放大变成了图(12),图(8)“压缩”而不是整体缩小变成了图(11),所以它们不是相似图形.而图(1)与图(9)、图(2)与图(4)、图(3)与图(10)、图(5)与图(7)的形状完全相同,所以它们是相似图形.
探索新知
解:
相似图形有:图(1)和图(9),图(2)和图(4),图(3)和图(10),图(5)和图(7).
探索新知
总 结
判断两个图形是否是相似图形的方法:
看两个图形的形状是否相同,即看其中一个图形是否是由另一个图形放大或缩小得到的,如果是,那么它们是相似图形,否则就不是相似图形.
典题精讲
1 下列图形不是相似图形的是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
C
典题精讲
2 下列说法中正确的是( )
A.对应角相等的多边形一定是相似多边形
B.对应边的比相等的多边形是相似多边形
C.边数相同的多边形是相似多边形
D.对应角相等、对应边成比例的多边形是相似多边形
D
典题精讲
3 如图,在三个矩形中,相似的是( )
A.甲和丙
B.甲和乙
C.乙和丙
D.甲、乙和丙
A
探索新知
2
知识点
相似多边形的性质
问题 1
如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.
探索新知
问题 2
例如,下图中的两个大小不同的四边形ABCD 和四边形A1B1C1D1中,∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,
因此四边形ABCD和四边形A1B1C1D1相似.
A
B
C
D
A
B
C
D
探索新知
归 纳
相似多边形的性质:相似多边形的对应边的比相等,
对应角相等.
作用:常用来求相似多边形中未知的边的长度和角的度数.
探索新知
如图,五边形ABCDE∽五边形A1B1C1D1E1,求C1D1的长和∠A的度数.
例 2
∵五边形ABCDE∽五边
形A1B1C1D1E1,
∴
∠E=∠E1=145°.
∴AB=15, A1B1=10, CD=21,
∴ 解得C1D1=14.
解:
探索新知
又∵∠B=130°,∠C=∠D=90°,
∵∠A=(5-2)×180°-130°-145°-2×90°=85°.
所以, C1D1=14 ,∠A=85°.
探索新知
总 结
利用相似多边形的性质求边长或角度,关键扣住“对
应”二字,找准对应边和对应角是解决问题的关键.需要
注意的是对应边是比相等,而对应角是直接相等.
典题精讲
1 若一个三角形三边之比为3∶5∶7,与它相似的三角形的最长边的长为21,则最短边的长为( )
A.15 B.10 C.9 D.3
2 如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是( )
A.2DE=3MN
B.3DE=2MN
C.3∠A=2∠F
D.2∠A=3∠F
C
B
探索新知
3
知识点
相似比
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.例如,放映电影时,投在屏幕上的画面就是胶片上图形的放大;用复印机把一个图形放大或缩小后所得的图形,都与原来的图形相似.下图中有2对图形,每对图形中的两个图形相似.其中较大(小)的图形可以看成是由较小 (大)的图形放大(缩小)得到的.
探索新知
上边的图形是相似图形,它们对应的比值有何关系呢?我们用尺子测量一下,看看.通过测量,我们发现每两个图形对应边的比值相等,我们把相似多边形对应边的比称为相似比.
1.相似比的定义:相似多边形对应边的比叫做它们的相似比.
2.要点精析:
(1)相似比与两个多边形的前后顺序有关;
(2)相似比为1的两个相似多边形为全等多边形.
探索新知
如图,把矩形ABCD 对折,折痕为MN,矩形DMNC 与矩形ABCD 相似,已知AB=4.
(1) 求AD的长;
(2)求矩形DMNC 与矩形ABCD 的相似比.
相似多边形的对应边的比相等,
其比值就是相似比.
例3
导引:
A
B
C
D
E
M
探索新知
(1)设AD=x,则
∵矩形DMNC 与矩形ABCD 相似,
(2)矩形DMNC 与矩形ABCD 的相似比为
解:
探索新知
总 结
利用相似多边形的性质求线段长及相似比的方法:
先找出与已知边、未知边相关的四条对应线段,再通过设未知数并用含未知数的式子表示其中的部分线段,最后通过相似多边形的对应边成比例建立方程进行计算.这种巧用方程思想的方法在相似多边形的计算中经常运用.
典题精讲
1 如果两个相似多边形的一组对应边长分别为3cm和2cm,那么它们的相似比是( )
A. B. C. D.
2 已知正方形ABCD与正方形DEFG 的边长分别是2 cm和4cm,则正方形ABCD与正方形DEFG 的相似比是__________.
C
学以致用
小试牛刀
1.两个多边形相似的条件是( )
A.对应角相等
B.对应边成比例
C.对应角相等或对应边成比例
D.对应角相等且对应边成比例
D
2.如图所示的两个四边形相似,则α=________°.
75
小试牛刀
3.若五边形ABCDE∽五边形A′B′C′D′E′,且AB=25 cm,A′B′=20 cm,则五边形A′B′C′D′E′与五边形ABCDE的相似比为________.
4.如图过点P 的两直线EF,MN 将矩形ABCD 分成甲、乙、丙、丁四个矩形,其中P 在AC上,且AP∶PC=AD∶AB=4∶3,下列对于矩形是否相似的判断,正确的是( )
A.甲、乙不相似 B.甲、丁不相似
C.丙、乙相似 D.丙、丁相似
A
小试牛刀
5.如图,四边形ABCD∽四边形GFEH,且∠A=∠G=70°,∠B=60°,∠E=120°,DC=24,HE=18,HG=21,求∠D,∠F 的大小和AD 的长.
小试牛刀
解:∵四边形ABCD∽四边形GFEH,
∴∠C=∠E=120°,∠F=∠B=60°.
∵∠A=70°,∠B=60°,
∴∠D=360°-∠A-∠B-∠C=360°-70°-60°-120°=110°.
∵四边形ABCD∽四边形GFEH,
解得AD=28,
∴∠D=110°,∠F=60°,AD=28.
小试牛刀
6.学生会举办一个校园摄影艺术展览会,小华和小刚准备将矩形的作品四周镶上一圈等宽的纸边,如图所示.两人在设计时发生了争执:小华要使内外两个矩形相似,感到这样视觉效果较好;小刚试了几次不能办到,表示这是不可能的.小红和小莉了解情况后,小红说这一要求只有当矩形作品是黄金矩形时才能做到,小莉则坚持只有当矩形作品是正方形时才能做到.请你动手试一试,说一说你的看法.
小试牛刀
解:只有当矩形作品是正方形时才能做到.
理由:设原矩形作品的一边为a,另一边为b,等宽的纸边宽为c.
若要使两矩形相似,则a∶b=(a+2c)∶(b+2c),
解得a=b,∴只有当矩形作品是正方形时才能使内外两个矩形相似.
课堂小结
课堂小结
知识总结 知识方法要点 关键总结 注意事项
相似多边形 (1)各对应角分别相等,各边成比例的两个多边形叫做相似多边形 (2)相似多边形对应边的比叫做相似比 (1)记两个多边形相似时,一定要把对应顶点的字母写在对应的位置.
(2)利用相似多边形的概念解题时,一定要找准各对应角、各对应边.
课堂小结
方法规律总结:
只有边数相同,各角分别相等,各边成比例,两个多边形才是相似多边形,据此判断两个多边形是否相似.
相似多边形的边数相同,各角分别相等,各边成比例,据此求两个相似多边形某些线段的长度或某些角的度数
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.7 相似多边形和图形的位似
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
你看下面的图形有什么特点 今天我们就来研究这个问题!
(1)
(2)
(3)
新课精讲
探索新知
1
知识点
相似多边形的定义
如图,在上、下两行的图形中,把你认为是相似图形的用线连起来.
在相似图形中,现阶段只研究相似多边形.
探索新知
归 纳
一般地,如果两个多边形的对应角相等、对应边成比例,那么这两个多边形就叫做相似多边形(similar polygons).
探索新知
1.定义:形状相同的图形叫做相似图形.
要点精析:
(1) “形状相同”是判定相似图形的唯一条件.
(2)相似图形之间的关系:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
(3)相似与全等的关系:当两个图形的形状相同、大小也相同时,它们是全等图形,全等图形是相似图形的特殊情况,即全等图形一定是相似图形,但相似图形不一定是全等图形,只有相似图形的大小相同时,它们才全等.
探索新知
2.易错警示:
(1)两个图形相似是指它们的形状相同,与它们的位置、大小无关;
(2)全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
探索新知
下图中的相似图形有哪些
例1
导引:
本题依据相似图形的定义求解.观察这些图形,虽然图(6)与图(12)、图(8)与图(11)极为相似,但是它们的形状不相同.图(6)“拉长”而不是整体放大变成了图(12),图(8)“压缩”而不是整体缩小变成了图(11),所以它们不是相似图形.而图(1)与图(9)、图(2)与图(4)、图(3)与图(10)、图(5)与图(7)的形状完全相同,所以它们是相似图形.
探索新知
解:
相似图形有:图(1)和图(9),图(2)和图(4),图(3)和图(10),图(5)和图(7).
探索新知
总 结
判断两个图形是否是相似图形的方法:
看两个图形的形状是否相同,即看其中一个图形是否是由另一个图形放大或缩小得到的,如果是,那么它们是相似图形,否则就不是相似图形.
典题精讲
1 下列图形不是相似图形的是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
C
典题精讲
2 下列说法中正确的是( )
A.对应角相等的多边形一定是相似多边形
B.对应边的比相等的多边形是相似多边形
C.边数相同的多边形是相似多边形
D.对应角相等、对应边成比例的多边形是相似多边形
D
典题精讲
3 如图,在三个矩形中,相似的是( )
A.甲和丙
B.甲和乙
C.乙和丙
D.甲、乙和丙
A
探索新知
2
知识点
相似多边形的性质
问题 1
如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.
探索新知
问题 2
例如,下图中的两个大小不同的四边形ABCD 和四边形A1B1C1D1中,∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,
因此四边形ABCD和四边形A1B1C1D1相似.
A
B
C
D
A
B
C
D
探索新知
归 纳
相似多边形的性质:相似多边形的对应边的比相等,
对应角相等.
作用:常用来求相似多边形中未知的边的长度和角的度数.
探索新知
如图,五边形ABCDE∽五边形A1B1C1D1E1,求C1D1的长和∠A的度数.
例 2
∵五边形ABCDE∽五边
形A1B1C1D1E1,
∴
∠E=∠E1=145°.
∴AB=15, A1B1=10, CD=21,
∴ 解得C1D1=14.
解:
探索新知
又∵∠B=130°,∠C=∠D=90°,
∵∠A=(5-2)×180°-130°-145°-2×90°=85°.
所以, C1D1=14 ,∠A=85°.
探索新知
总 结
利用相似多边形的性质求边长或角度,关键扣住“对
应”二字,找准对应边和对应角是解决问题的关键.需要
注意的是对应边是比相等,而对应角是直接相等.
典题精讲
1 若一个三角形三边之比为3∶5∶7,与它相似的三角形的最长边的长为21,则最短边的长为( )
A.15 B.10 C.9 D.3
2 如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是( )
A.2DE=3MN
B.3DE=2MN
C.3∠A=2∠F
D.2∠A=3∠F
C
B
探索新知
3
知识点
相似比
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.例如,放映电影时,投在屏幕上的画面就是胶片上图形的放大;用复印机把一个图形放大或缩小后所得的图形,都与原来的图形相似.下图中有2对图形,每对图形中的两个图形相似.其中较大(小)的图形可以看成是由较小 (大)的图形放大(缩小)得到的.
探索新知
上边的图形是相似图形,它们对应的比值有何关系呢?我们用尺子测量一下,看看.通过测量,我们发现每两个图形对应边的比值相等,我们把相似多边形对应边的比称为相似比.
1.相似比的定义:相似多边形对应边的比叫做它们的相似比.
2.要点精析:
(1)相似比与两个多边形的前后顺序有关;
(2)相似比为1的两个相似多边形为全等多边形.
探索新知
如图,把矩形ABCD 对折,折痕为MN,矩形DMNC 与矩形ABCD 相似,已知AB=4.
(1) 求AD的长;
(2)求矩形DMNC 与矩形ABCD 的相似比.
相似多边形的对应边的比相等,
其比值就是相似比.
例3
导引:
A
B
C
D
E
M
探索新知
(1)设AD=x,则
∵矩形DMNC 与矩形ABCD 相似,
(2)矩形DMNC 与矩形ABCD 的相似比为
解:
探索新知
总 结
利用相似多边形的性质求线段长及相似比的方法:
先找出与已知边、未知边相关的四条对应线段,再通过设未知数并用含未知数的式子表示其中的部分线段,最后通过相似多边形的对应边成比例建立方程进行计算.这种巧用方程思想的方法在相似多边形的计算中经常运用.
典题精讲
1 如果两个相似多边形的一组对应边长分别为3cm和2cm,那么它们的相似比是( )
A. B. C. D.
2 已知正方形ABCD与正方形DEFG 的边长分别是2 cm和4cm,则正方形ABCD与正方形DEFG 的相似比是__________.
C
学以致用
小试牛刀
1.两个多边形相似的条件是( )
A.对应角相等
B.对应边成比例
C.对应角相等或对应边成比例
D.对应角相等且对应边成比例
D
2.如图所示的两个四边形相似,则α=________°.
75
小试牛刀
3.若五边形ABCDE∽五边形A′B′C′D′E′,且AB=25 cm,A′B′=20 cm,则五边形A′B′C′D′E′与五边形ABCDE的相似比为________.
4.如图过点P 的两直线EF,MN 将矩形ABCD 分成甲、乙、丙、丁四个矩形,其中P 在AC上,且AP∶PC=AD∶AB=4∶3,下列对于矩形是否相似的判断,正确的是( )
A.甲、乙不相似 B.甲、丁不相似
C.丙、乙相似 D.丙、丁相似
A
小试牛刀
5.如图,四边形ABCD∽四边形GFEH,且∠A=∠G=70°,∠B=60°,∠E=120°,DC=24,HE=18,HG=21,求∠D,∠F 的大小和AD 的长.
小试牛刀
解:∵四边形ABCD∽四边形GFEH,
∴∠C=∠E=120°,∠F=∠B=60°.
∵∠A=70°,∠B=60°,
∴∠D=360°-∠A-∠B-∠C=360°-70°-60°-120°=110°.
∵四边形ABCD∽四边形GFEH,
解得AD=28,
∴∠D=110°,∠F=60°,AD=28.
小试牛刀
6.学生会举办一个校园摄影艺术展览会,小华和小刚准备将矩形的作品四周镶上一圈等宽的纸边,如图所示.两人在设计时发生了争执:小华要使内外两个矩形相似,感到这样视觉效果较好;小刚试了几次不能办到,表示这是不可能的.小红和小莉了解情况后,小红说这一要求只有当矩形作品是黄金矩形时才能做到,小莉则坚持只有当矩形作品是正方形时才能做到.请你动手试一试,说一说你的看法.
小试牛刀
解:只有当矩形作品是正方形时才能做到.
理由:设原矩形作品的一边为a,另一边为b,等宽的纸边宽为c.
若要使两矩形相似,则a∶b=(a+2c)∶(b+2c),
解得a=b,∴只有当矩形作品是正方形时才能使内外两个矩形相似.
课堂小结
课堂小结
知识总结 知识方法要点 关键总结 注意事项
相似多边形 (1)各对应角分别相等,各边成比例的两个多边形叫做相似多边形 (2)相似多边形对应边的比叫做相似比 (1)记两个多边形相似时,一定要把对应顶点的字母写在对应的位置.
(2)利用相似多边形的概念解题时,一定要找准各对应角、各对应边.
课堂小结
方法规律总结:
只有边数相同,各角分别相等,各边成比例,两个多边形才是相似多边形,据此判断两个多边形是否相似.
相似多边形的边数相同,各角分别相等,各边成比例,据此求两个相似多边形某些线段的长度或某些角的度数
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
