冀教版(新)九上-26.1 锐角三角函数 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-26.1 锐角三角函数 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览







文档简介
(共40张PPT)
26.1 锐角三角函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
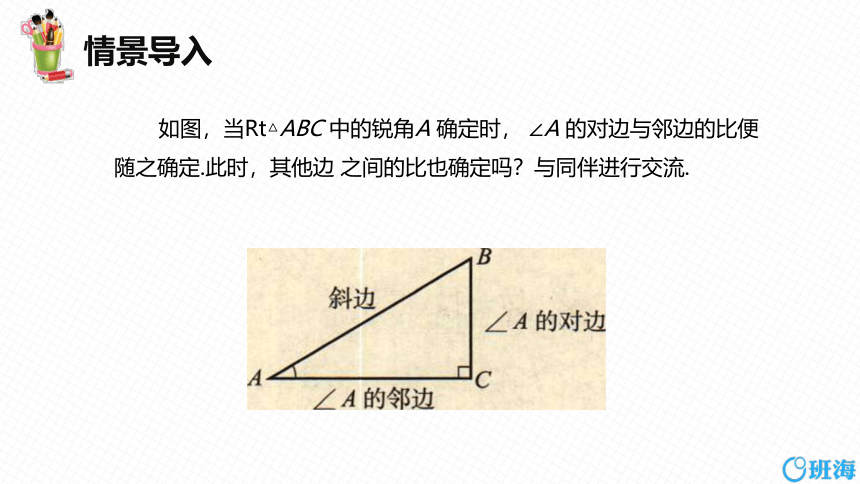
如图,当Rt△ABC 中的锐角A 确定时, ∠A 的对边与邻边的比便随之确定.此时,其他边 之间的比也确定吗?与同伴进行交流.
新课精讲
探索新知
1
知识点
正弦
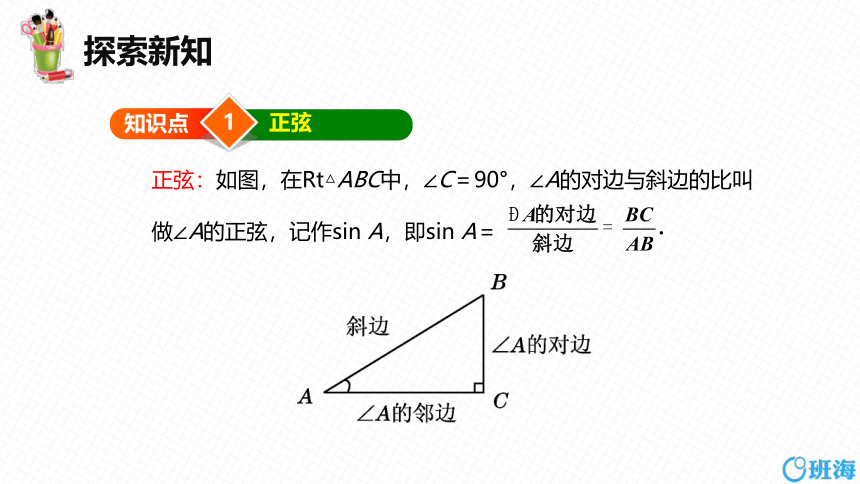
正弦:如图,在Rt△ABC中,∠C=90°,∠A的对边与斜边的比叫做∠A的正弦,记作sin A,即sin A=
探索新知
问 题
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡的坡角 (∠A)为30°,为使出水口的高度为35 m,需要准备多长的水管?
探索新知
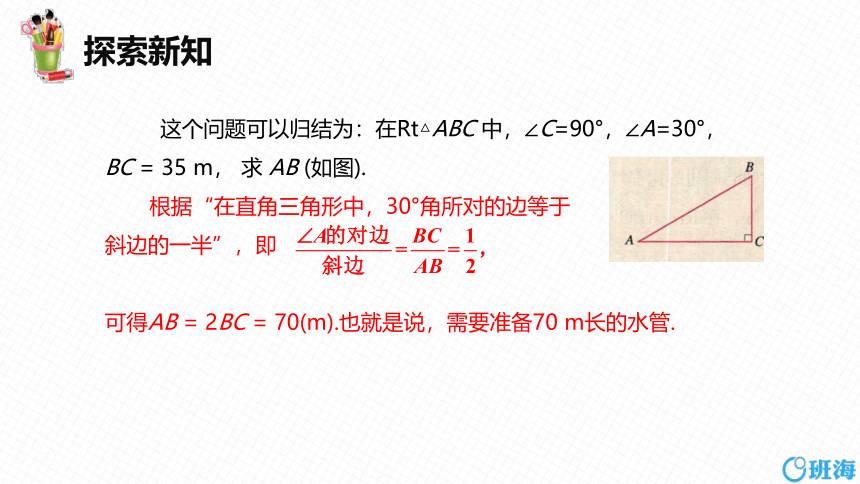
这个问题可以归结为:在Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m, 求 AB (如图).
根据“在直角三角形中,30°角所对的边等于
斜边的一半”,即
可得AB = 2BC = 70(m).也就是说,需要准备70 m长的水管.
探索新知
思考1:
在上面的问题中,如果出水口的高度为50 m,那么需要准备多长的水管?
在上面求AB (所需水管的长度)的过程中,我们用到了结论:在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
探索新知
思考2:
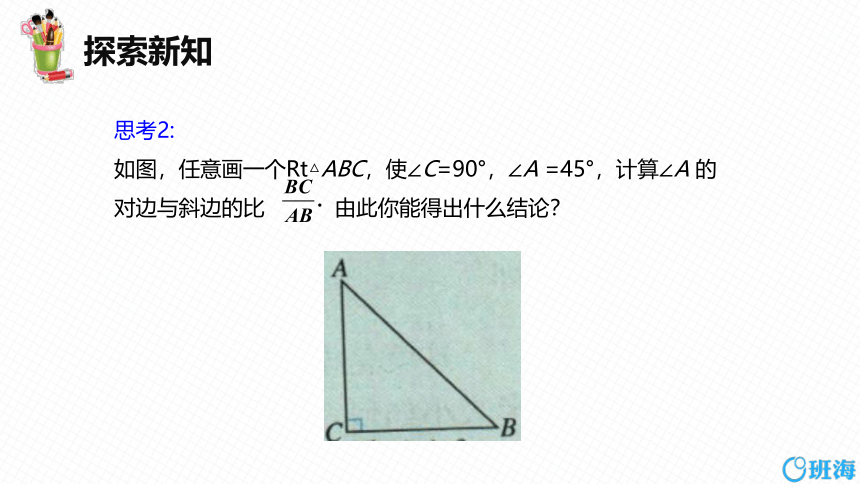
如图,任意画一个Rt△ABC,使∠C=90°,∠A =45°,计算∠A 的对边与斜边的比 由此你能得出什么结论?
探索新知
如图,在Rt△ABC 中,∠C=90°,因为∠A= 45°,所以Rt△ABC是等腰直角三角形.由勾股定理得
AB 2=AC 2+BC 2 = 2BC 2 ,
AB = BC.
因此
即在直角三角形中,当一个锐角等于45°时,无论这个直角三角形大小如何, 这个角的对边与斜边的比都等于
探索新知
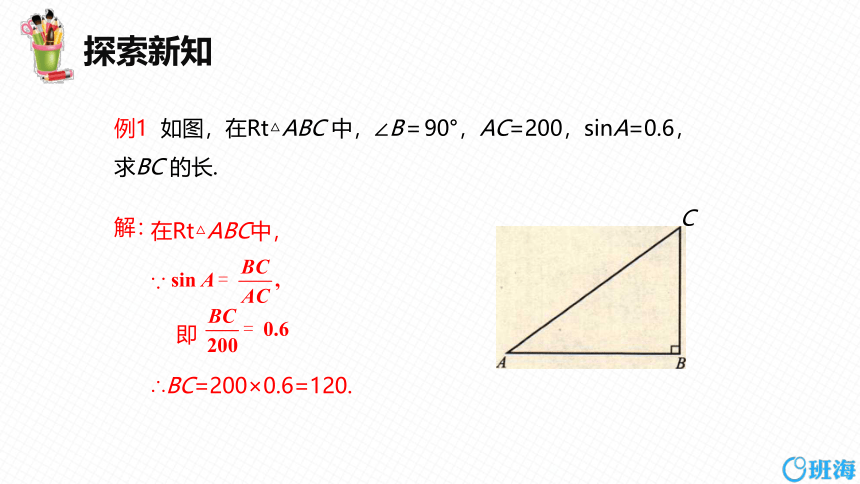
例1 如图,在Rt△ABC 中,∠B=90°,AC=200,sinA=0.6,求BC 的长.
在Rt△ABC中,
∵
即
∴BC=200×0.6=120.
解:
C
典题精讲
在Rt△ABC 中,∠C=90°,sin A= ,BC=6,则AB=( )
A.4 B.6
C.8 D.10
D
典题精讲
如图,△ABC 的顶点是正方形网格的格点,则sin A 的值为( )
A. B.
C. D.
B
探索新知
2
知识点
余弦
余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻边与斜边的比叫做∠A的余弦,记作cos A,即cos A=
探索新知
例2 如图,在Rt△ABC 中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC 中,已知两直角边长,可先用勾股定理求斜边长,再利用定义分别求出sin A,cos A的值.
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=
探索新知
总 结
在直角三角形中,求锐角的正弦和余弦时,一定要根据正弦和余弦的定义求解.其中未知边的长度往往借助勾股定理进行求解.
探索新知
例3 如图,在Rt△ABC 中,∠C=90°,sin A= BC=40,
求△ABC 的周长和面积.
导引:
已知BC=40,求△ABC的周长,
则还需要求出其他两边的长,借
助sin A的值可求出AB的长,再
利用勾股定理求出AC的长即可,
直角三角形的面积等于两直角边
长乘积的一半.
探索新知
解:∵sin A= ∴AB=
∵BC=40,sin A= ,∴AB=50.
又∵AC=
∴△ABC 的周长为AB+AC+BC=120,
△ABC的面积为 BC·AC= ×40×30=600.
探索新知
总 结
正弦的定义表达式sin A= 可根据解题需要变形为
BC=AB sin A或AB=
余弦的定义表达式cos A= 也可变形为
AC=AB cos A或AB= .
典题精讲
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则图中∠ABC 的余弦值是( )
A.2 B.
C. D.
D
典题精讲
如图,以O为圆心,半径为1的弧交坐标轴于A,B 两点,P是AB上一点(不与A,B 重合),连接OP,设∠POB=α,则点P 的坐标是( )
A.(sin α,sin α)
B.(cos α,cos α)
C.(cos α,sin α)
D.(sin α,cos α)
︵
C
探索新知
3
知识点
锐角三角函数的取值范围
1. 锐角三角函数的定义:
定义:如图,在Rt△ABC 中,∠C=90°,∠A,
∠B,∠C 的对边分别为a,b,c,则有sin A= ,
cos A= tan A= 我们把sin A,cos A,tan A
叫做∠A的三角函数,即
锐角A的正弦、余弦、正
切叫做∠A的三角函数.
探索新知
2. 锐角三角函数的取值范围:
在Rt△ABC 中,因为各边边长都是正数,且斜边边长大于直角边边长,所以对于锐角A,有tan A>0,0<sin A<1,0<cos A<1.
典题精讲
若α 是锐角,sin α=3m-2,则m 的取值范围是( )
A. <m<1 B.2<m<3
C.0<m<1 D.m>
如果0°<∠A<90°,并且cos A是方程 (x-0.35)=0的一个根,那么cos A=___________.
A
0.35
探索新知
4
知识点
特殊角(30°,45°,60°)的正弦、余弦值
1.30°,45°,60°角的函数值如下表:
30° 45° 60°
sin α
cos α
角α
三角函数值
三角函数
典题精讲
在△ABC中,∠A,∠B都是锐角,且sin A= ,cos B= ,则△ABC的形状是( )
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
B
学以致用
小试牛刀
如图,在Rt△ABC 中,∠C=90°,求sin A 和sin B 的值.
解:由勾股定理得
所以
小试牛刀
解:由勾股定理得
∴
小试牛刀
在Rt△ABC 中,∠C=90°,AB=13,AC=5,则sin A 的值为( )
B. C. D.
B
2
把Rt△ABC 三边的长度都扩大为原来的3倍, 则锐角∠A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
A
小试牛刀
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α 的值是( )
A.
B.
C.
D.
C
4
小试牛刀
5 在Rt△ABC中,∠C=90°,∠A=90°,求sin A 的值.
解:如图.
∠B=90°-∠A=90°-60°=30°.
∴sin B=sin30°=
设AC=a,则AB=2a,
∴
小试牛刀
6 在Rt△ABC中,∠C=90°,AC=9,sin B= ,则AB 的长等于( )
A.15 B.12 C.9 D.6
7 在Rt△ABC 中,∠C=90°,若AB=4,sin A= ,则斜边上的高等于( )
A. B. C. D.
A
B
小试牛刀
8.在直角三角形ABC 中,AC=4,BC=3,求sin A的值.
解:
此题分两种情况:①当AC,BC 为两直角边时,AB=
=5,所以sin A= ;
②当BC 为直角边,AC 为斜边时,sin A= .
小试牛刀
9 如图,在等腰三角形ABC 中,AC=BC=10,AB=12,以BC 为直径作⊙O 交AB于点D,交AC 于点G,DF⊥AC,垂足为F,交CB 的延长线于点E.
(1)求证:直线EF是⊙O 的切线;
(2)求cos E的值.
小试牛刀
(1)证明:如图,连接OD,CD. ∵BC 是直径,
∴CD⊥AB.∵AC=BC,∴D是AB
的中点.又∵O为CB 的中点,∴OD∥AC.
∵DF⊥AC,∴OD⊥EF,∴EF是⊙O 的切线.
(2)解:如图,连接BG.∵BC 是直径,∴∠BGC=90°.
在Rt△ACD 中,DC= =8.
∵AB·CD=2S△ABC=AC·BG,
∴BG=
∵BG⊥AC,DF⊥AC,∴BG∥EF,∴∠E=∠CBG.
∴cos E=cos ∠CBG=
课堂小结
课堂小结
1.正弦的定义
2.余弦的定义
3.求锐角三角函数值的三种方法:
(1)在直角三角形里,确定各个边,根据定义直接求出.
(2)利用相似、全等等关系,寻找与所求角相等的角(若该角的三角函数值知道或者易求).
(3)利用互余的两个角间的特殊关系求.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
26.1 锐角三角函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,当Rt△ABC 中的锐角A 确定时, ∠A 的对边与邻边的比便随之确定.此时,其他边 之间的比也确定吗?与同伴进行交流.
新课精讲
探索新知
1
知识点
正弦
正弦:如图,在Rt△ABC中,∠C=90°,∠A的对边与斜边的比叫做∠A的正弦,记作sin A,即sin A=
探索新知
问 题
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡的坡角 (∠A)为30°,为使出水口的高度为35 m,需要准备多长的水管?
探索新知
这个问题可以归结为:在Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m, 求 AB (如图).
根据“在直角三角形中,30°角所对的边等于
斜边的一半”,即
可得AB = 2BC = 70(m).也就是说,需要准备70 m长的水管.
探索新知
思考1:
在上面的问题中,如果出水口的高度为50 m,那么需要准备多长的水管?
在上面求AB (所需水管的长度)的过程中,我们用到了结论:在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
探索新知
思考2:
如图,任意画一个Rt△ABC,使∠C=90°,∠A =45°,计算∠A 的对边与斜边的比 由此你能得出什么结论?
探索新知
如图,在Rt△ABC 中,∠C=90°,因为∠A= 45°,所以Rt△ABC是等腰直角三角形.由勾股定理得
AB 2=AC 2+BC 2 = 2BC 2 ,
AB = BC.
因此
即在直角三角形中,当一个锐角等于45°时,无论这个直角三角形大小如何, 这个角的对边与斜边的比都等于
探索新知
例1 如图,在Rt△ABC 中,∠B=90°,AC=200,sinA=0.6,求BC 的长.
在Rt△ABC中,
∵
即
∴BC=200×0.6=120.
解:
C
典题精讲
在Rt△ABC 中,∠C=90°,sin A= ,BC=6,则AB=( )
A.4 B.6
C.8 D.10
D
典题精讲
如图,△ABC 的顶点是正方形网格的格点,则sin A 的值为( )
A. B.
C. D.
B
探索新知
2
知识点
余弦
余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻边与斜边的比叫做∠A的余弦,记作cos A,即cos A=
探索新知
例2 如图,在Rt△ABC 中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC 中,已知两直角边长,可先用勾股定理求斜边长,再利用定义分别求出sin A,cos A的值.
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=
探索新知
总 结
在直角三角形中,求锐角的正弦和余弦时,一定要根据正弦和余弦的定义求解.其中未知边的长度往往借助勾股定理进行求解.
探索新知
例3 如图,在Rt△ABC 中,∠C=90°,sin A= BC=40,
求△ABC 的周长和面积.
导引:
已知BC=40,求△ABC的周长,
则还需要求出其他两边的长,借
助sin A的值可求出AB的长,再
利用勾股定理求出AC的长即可,
直角三角形的面积等于两直角边
长乘积的一半.
探索新知
解:∵sin A= ∴AB=
∵BC=40,sin A= ,∴AB=50.
又∵AC=
∴△ABC 的周长为AB+AC+BC=120,
△ABC的面积为 BC·AC= ×40×30=600.
探索新知
总 结
正弦的定义表达式sin A= 可根据解题需要变形为
BC=AB sin A或AB=
余弦的定义表达式cos A= 也可变形为
AC=AB cos A或AB= .
典题精讲
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则图中∠ABC 的余弦值是( )
A.2 B.
C. D.
D
典题精讲
如图,以O为圆心,半径为1的弧交坐标轴于A,B 两点,P是AB上一点(不与A,B 重合),连接OP,设∠POB=α,则点P 的坐标是( )
A.(sin α,sin α)
B.(cos α,cos α)
C.(cos α,sin α)
D.(sin α,cos α)
︵
C
探索新知
3
知识点
锐角三角函数的取值范围
1. 锐角三角函数的定义:
定义:如图,在Rt△ABC 中,∠C=90°,∠A,
∠B,∠C 的对边分别为a,b,c,则有sin A= ,
cos A= tan A= 我们把sin A,cos A,tan A
叫做∠A的三角函数,即
锐角A的正弦、余弦、正
切叫做∠A的三角函数.
探索新知
2. 锐角三角函数的取值范围:
在Rt△ABC 中,因为各边边长都是正数,且斜边边长大于直角边边长,所以对于锐角A,有tan A>0,0<sin A<1,0<cos A<1.
典题精讲
若α 是锐角,sin α=3m-2,则m 的取值范围是( )
A. <m<1 B.2<m<3
C.0<m<1 D.m>
如果0°<∠A<90°,并且cos A是方程 (x-0.35)=0的一个根,那么cos A=___________.
A
0.35
探索新知
4
知识点
特殊角(30°,45°,60°)的正弦、余弦值
1.30°,45°,60°角的函数值如下表:
30° 45° 60°
sin α
cos α
角α
三角函数值
三角函数
典题精讲
在△ABC中,∠A,∠B都是锐角,且sin A= ,cos B= ,则△ABC的形状是( )
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
B
学以致用
小试牛刀
如图,在Rt△ABC 中,∠C=90°,求sin A 和sin B 的值.
解:由勾股定理得
所以
小试牛刀
解:由勾股定理得
∴
小试牛刀
在Rt△ABC 中,∠C=90°,AB=13,AC=5,则sin A 的值为( )
B. C. D.
B
2
把Rt△ABC 三边的长度都扩大为原来的3倍, 则锐角∠A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
A
小试牛刀
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α 的值是( )
A.
B.
C.
D.
C
4
小试牛刀
5 在Rt△ABC中,∠C=90°,∠A=90°,求sin A 的值.
解:如图.
∠B=90°-∠A=90°-60°=30°.
∴sin B=sin30°=
设AC=a,则AB=2a,
∴
小试牛刀
6 在Rt△ABC中,∠C=90°,AC=9,sin B= ,则AB 的长等于( )
A.15 B.12 C.9 D.6
7 在Rt△ABC 中,∠C=90°,若AB=4,sin A= ,则斜边上的高等于( )
A. B. C. D.
A
B
小试牛刀
8.在直角三角形ABC 中,AC=4,BC=3,求sin A的值.
解:
此题分两种情况:①当AC,BC 为两直角边时,AB=
=5,所以sin A= ;
②当BC 为直角边,AC 为斜边时,sin A= .
小试牛刀
9 如图,在等腰三角形ABC 中,AC=BC=10,AB=12,以BC 为直径作⊙O 交AB于点D,交AC 于点G,DF⊥AC,垂足为F,交CB 的延长线于点E.
(1)求证:直线EF是⊙O 的切线;
(2)求cos E的值.
小试牛刀
(1)证明:如图,连接OD,CD. ∵BC 是直径,
∴CD⊥AB.∵AC=BC,∴D是AB
的中点.又∵O为CB 的中点,∴OD∥AC.
∵DF⊥AC,∴OD⊥EF,∴EF是⊙O 的切线.
(2)解:如图,连接BG.∵BC 是直径,∴∠BGC=90°.
在Rt△ACD 中,DC= =8.
∵AB·CD=2S△ABC=AC·BG,
∴BG=
∵BG⊥AC,DF⊥AC,∴BG∥EF,∴∠E=∠CBG.
∴cos E=cos ∠CBG=
课堂小结
课堂小结
1.正弦的定义
2.余弦的定义
3.求锐角三角函数值的三种方法:
(1)在直角三角形里,确定各个边,根据定义直接求出.
(2)利用相似、全等等关系,寻找与所求角相等的角(若该角的三角函数值知道或者易求).
(3)利用互余的两个角间的特殊关系求.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
