冀教版(新)九上-26.2 锐角三角函数的计算【优质课件】
文档属性
| 名称 | 冀教版(新)九上-26.2 锐角三角函数的计算【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览











文档简介
(共41张PPT)
26.2 锐角三角函数的计算
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
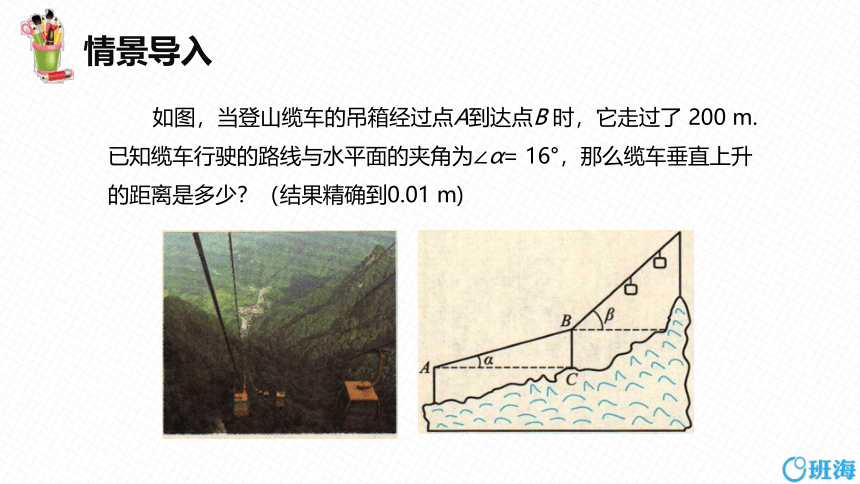
如图,当登山缆车的吊箱经过点A到达点B 时,它走过了 200 m.已知缆车行驶的路线与水平面的夹角为∠α= 16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
情景导入
在Rt△ABC 中,∠ACB=90 °,BC=AB sin 16°.你知道sin16°是多少吗?我们可以借助科学计算器求锐角的三角函数值. 怎样用科学计算器求三角函数值呢?
新课精讲
探索新知
1
知识点
用计算器求已知锐角的三角函数值
1.计算器的使用方法:
(1)求整数度数的锐角三角函数值,在科学计算器的面板上涉及三角函数的键有sin ,cos 和tan ,当我们计算整数度数的某锐角的三角函数值时,可选按这三个键之一,然后再从高位到低位依次按出表示度数的键,然后按=键,屏幕上就会显示出结果.
探索新知
(2)求非整数度数的锐角三角函数值,若度数的单位是用度、分、秒表示的,在用科学计算器计算其三角函数值时,同样先按sin ,cos 或tan 键,然后从高位到低位依次按出表示度的键,再按°’”键,然后,从高位到低位依次按出表示分的键,再按°’”键,然后,从高位到低位依次按出表示秒的键,再按°’”键,最后按=键,屏幕上就会显示出结果.
探索新知
2.说明:
(1)用计算器求三角函数值时,结果一般有10个数位,也有的计算器会显示11个数位.如无特别说明,计算结果一般精确到万分位;
(2)不同的计算器按键方式不同,因此在使用之前要首先了解计算器的功能与使用方法.
探索新知
例1 用计算器计算:(结果精确到万分位)
(1)sin 26°≈ ;
(2) sin82°48′15″≈________.
导引:
0.4384
0.9921
已知锐角求三角函数值,按照正确的按键顺序按键,将屏幕显示的结果按要求取近似值即可.
探索新知
总 结
(1)依次按sin 2 6 =键,得到数据再精确到万分位即可;
(2)依次按sin 8 2 °’ ” 48°’ ”15°’ ”=键,得到数据再精确到万分位即可.
探索新知
例2 已知在Rt△ABC中,∠C=90°,若∠A=23°,斜
边c=14,求∠A 的对边a 的长.(结果精确到0.01).
c 是斜边,而a 是∠A的对边,故可利用∠A 的正弦求a.
由sin A= 则a=c · sin A=14sin 23°,利用计算器
计算得a≈5.47.
导引:
解:
探索新知
总 结
对于不是特殊角的三角函数,一般只能利用计算
器进行计算.注意结果要符合题目的精确度要求.
典题精讲
如图,是我们数学课上采用的科学计算器面板,利用该型号计算器计算cos 55°,按键顺序正确的是( )
C
典题精讲
利用计算器求sin 30°时,依次按键sin30°′″=,则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1
A
探索新知
2
知识点
用计算器求已知三角函数值的对应角
想一想
为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建 了 40 m长的斜道(如图).这条斜道的倾斜角是多少?
探索新知
1.已知三角函数值,用计算器求角度,需要用到sin ,
cos ,tan 键的第二功能“sin-1,cos-1,tan-1”和
SHIFT 键.
2.具体操作步骤是:先按SHIFT 键,再按sin ,cos ,
tan 键之一,再依次输入三角函数值,最后按=键,
则屏幕上就会显示出结果.
探索新知
拓展:
(1)上面得出的结果是以“度”为单位的,再按°’”键
即可显示以“度、分、秒”为单位的结果.
(2)求角度的计算结果,如没有特别说明,一般精确到1″.
3.易错警示:注意由值求角必须保证按键顺序正确.
探索新知
例3 根据下列条件求锐角A 的度数:(结果精确到1′)
(1)sin A=0.732 1;(2)cos A=0.218 7;(3)tan A=3.527.
导引:利用sin ,cos ,tan 键的第二功能计算,即先按SHIFT键,再按sin或cos或tan键,然后输入三角函数值,最后按=键,即可显示结果.
探索新知
解:
(1)先按SHIFT sin 0.7321=键,显示:47.062 734 57,再按°’”键,即可显示47°3′45.84″,所以∠A≈47°4′.
(2)先按 SHIFT cos 0.2187=键,显示:77.367 310 78,再按°’”键,显示77°22′2.32″,所以∠A≈77°22′.
(3)先按 SHIFT tan 3.527=键,显示:74.170 530 81,再按°’”键,显示74°10′13.91″,所以∠A≈74°10′.
探索新知
总 结
由值求角,计算器显示的角度的单位是“度”,一般需要化为用“度、分、秒”表示的形式,用°’”键可实现两者间的转换.
典题精讲
已知α为锐角,且tan α=3.387,下列各值中与α 最接近的是( )
A.73°33′ B.73°27′ C.16°27′ D.16°21′
在△ABC 中,∠C=90°,BC=5,AB=13,用科学计算器求∠A 约等于( )
A.24°38′ B.65°22′ C.67°23′ D.22°37′
A
D
典题精讲
如图,有一滑梯AB,其水平宽度AC 为5.3 m,铅直高度BC 为2.8 m,则∠A的度数约为________(用科学计算器计算,结果精确到0.1°).
27.8
探索新知
3
知识点
用计算器探究三角函数的性质
三角函数值的大小有锐角的度数决定,与其在哪个直角三角形中无关,具体来说:
(1)tan A随着∠A的增大而增大,∠A越接近90°,tanA的值就增加得越快,tan A可以等于任何一个正数.
(2)sin A的值随着锐角A的增大而增大;cos A的值随着锐角A的增大而减小.
探索新知
例4 已知α,β 为锐角,且cos α 是方程2x2+5x-3=0的一个根,cos β≥cos α,试求α 的度数及β 的取值范围.
先求出方程2x2+5x-3=0的根,从而得到cos α 的值,再根据特殊角的三角函数值求出α 的度数,最后根据锐角三角函数的增减性确定β 的取值范围.
导引:
探索新知
解方程2x 2+5x-3=0,得x1=-3,x2=
∵0<cos α<1,且cos α 是方程2x 2+5x-3=0的一个根,
∴cos α=
∵cos 60°= ∴α=60°.
∵β 为锐角,cos β≥cos α,∴cos β≥cos 60°.
又∵锐角的余弦值随角的度数的增大而减小,
∴0°<β≤60°.
解:
探索新知
总 结
解方程,由特殊角的三角函数值可知α 的度数,再利用锐角与其余弦值的关系,通过比较得到β 的取值范围.
典题精讲
在Rt△ABC 中,∠C=90°,下列各式中正确的是 ( )
A.sin A=sin B B.tan A=tan B
C.sin A=cos B D.cos A=cos B
用计算器比较tan 25°,sin 27°,cos 26°的大小关系是( )
A.tan 25°B.tan 25°C.sin 27°D.cos 26°C
C
典题精讲
用计算器求sin 15°,sin 25°,sin 35°,sin 45°,sin 55°,sin 65°,sin 75°,sin 85°的值,研究sin α的值随锐角变化的规律,根据这个规律判断:
若A.30°<α<60° B.30°<α<90°
C.0°<α<60° D.60°<α<90°
A
学以致用
小试牛刀
1.计算sin245°+cos 30°·tan 60°,其结果是( )
A.2 B.1 C. D.
2.下列各式中正确的是( )
A.sin 60°=
B.cos 45°+sin 45°=
C.sin 60°=sin(2×30°)=2sin 30°
D.tan 60°+tan 30°=2
B
A
小试牛刀
3.用计算器求下列锐角三角函数值:
(1)sin 20°,cos 70°; sin 35°, cos 55°;sin15°32′,cos74°28′;
(2)tan 3° 8',tan 80° 25′43".
(1)sin 20°≈0.342 0,cos 70°≈0.342 0;
sin 35°≈0.573 6,cos 55°≈0.573 6;
sin 15°32′≈0.267 8,cos 74°28′≈0.267 8.
(2)tan 3°8′≈0.054 7,tan 80°25′43″≈5.930 4.
解:
小试牛刀
4.用计算器计算cos 44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
5.用计算器验证,下列等式正确的是( )
A.sin 18°24′+sin 35°36′=sin 54°
B.sin 65°54′-sin 35°54′=sin 30°
C.2sin 15°30′=sin 31°
D.sin 72°18′-sin 12°18′=sin 47°42′
B
D
小试牛刀
6.为了方便行人推车过某天桥,市政府在10 m高的天桥一侧修建了40 m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. 2ndF sin 0 · 2 5 =
B. sin 2ndF 0 · 2 5 =
C. sin 0 · 2 5 =
D. 2ndF cos 0 · 2 5 =
A
小试牛刀
7.(1)如图①②,锐角的正弦值和余弦值都随着锐角的变化而化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.
小试牛刀
(3)比较大小(在横线上填写“<”“>”或“=”):
若α=45°,则sin α________cos α;
若α<45°,则sin α________cos α;
若α>45°,则sin α________cos α.
(4)利用互为余角的两个角的正弦值和余弦值的关系,试比较下列正弦值和余弦值的大小:sin 10°,cos 30°,sin 50°,cos 70°.
(1)锐角的正弦值随角度的增大而增大,余弦值随角度的
增大而减小.
(2)sin 18°cos 88°(4)sin 10°解:
<
=
>
小试牛刀
8.如图,一艘海轮在A点时测得灯塔C 在它的北偏东42°方向上,它沿正东方向航行80海里后到达B 处,此时灯塔C 在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C 的最短距离(结果精确到0.1);
(2)求海轮在B 处时与灯塔C 的距离(结果保留整数).
(参考数据:sin 55°≈0.819,cos 55°≈0.574,
tan 55°≈1.428,tan 42°≈0.900,
tan 35°≈0.700,tan 48°≈1.111)
小试牛刀
解:
(1)如图,过C 作AB的垂线,垂足为D,
根据题意可得:∠ACD=42°,∠BCD
=55°.设CD 的长为x 海里,
在Rt△ACD 中,tan 42°= ,则AD=x ·tan 42°海里,
在Rt△BCD 中,tan 55°= ,则BD=x ·tan 55°海里.
∵AB=80海里,∴AD+BD=80海里,
∴x ·tan 42°+x ·tan 55°=80,解得x≈34.4,
即海轮在航行过程中与灯塔C 的最短距离约是34.4海里.
(2)在Rt△BCD 中,cos 55°= ,
∴BC= ≈60(海里),
即海轮在B 处时与灯塔C 的距离约是60海里.
课堂小结
课堂小结
1.利用计算器可求锐角的三角函数值,按键顺序:先按
sin键或cos键或tan键,再按角度值,最后按=键,就
可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺序:
先按SHIFT键,再按sin键或cos键或tan键,然后输入
三角函数值,最后按=键,就可求出相应角度.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
26.2 锐角三角函数的计算
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,当登山缆车的吊箱经过点A到达点B 时,它走过了 200 m.已知缆车行驶的路线与水平面的夹角为∠α= 16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
情景导入
在Rt△ABC 中,∠ACB=90 °,BC=AB sin 16°.你知道sin16°是多少吗?我们可以借助科学计算器求锐角的三角函数值. 怎样用科学计算器求三角函数值呢?
新课精讲
探索新知
1
知识点
用计算器求已知锐角的三角函数值
1.计算器的使用方法:
(1)求整数度数的锐角三角函数值,在科学计算器的面板上涉及三角函数的键有sin ,cos 和tan ,当我们计算整数度数的某锐角的三角函数值时,可选按这三个键之一,然后再从高位到低位依次按出表示度数的键,然后按=键,屏幕上就会显示出结果.
探索新知
(2)求非整数度数的锐角三角函数值,若度数的单位是用度、分、秒表示的,在用科学计算器计算其三角函数值时,同样先按sin ,cos 或tan 键,然后从高位到低位依次按出表示度的键,再按°’”键,然后,从高位到低位依次按出表示分的键,再按°’”键,然后,从高位到低位依次按出表示秒的键,再按°’”键,最后按=键,屏幕上就会显示出结果.
探索新知
2.说明:
(1)用计算器求三角函数值时,结果一般有10个数位,也有的计算器会显示11个数位.如无特别说明,计算结果一般精确到万分位;
(2)不同的计算器按键方式不同,因此在使用之前要首先了解计算器的功能与使用方法.
探索新知
例1 用计算器计算:(结果精确到万分位)
(1)sin 26°≈ ;
(2) sin82°48′15″≈________.
导引:
0.4384
0.9921
已知锐角求三角函数值,按照正确的按键顺序按键,将屏幕显示的结果按要求取近似值即可.
探索新知
总 结
(1)依次按sin 2 6 =键,得到数据再精确到万分位即可;
(2)依次按sin 8 2 °’ ” 48°’ ”15°’ ”=键,得到数据再精确到万分位即可.
探索新知
例2 已知在Rt△ABC中,∠C=90°,若∠A=23°,斜
边c=14,求∠A 的对边a 的长.(结果精确到0.01).
c 是斜边,而a 是∠A的对边,故可利用∠A 的正弦求a.
由sin A= 则a=c · sin A=14sin 23°,利用计算器
计算得a≈5.47.
导引:
解:
探索新知
总 结
对于不是特殊角的三角函数,一般只能利用计算
器进行计算.注意结果要符合题目的精确度要求.
典题精讲
如图,是我们数学课上采用的科学计算器面板,利用该型号计算器计算cos 55°,按键顺序正确的是( )
C
典题精讲
利用计算器求sin 30°时,依次按键sin30°′″=,则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1
A
探索新知
2
知识点
用计算器求已知三角函数值的对应角
想一想
为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建 了 40 m长的斜道(如图).这条斜道的倾斜角是多少?
探索新知
1.已知三角函数值,用计算器求角度,需要用到sin ,
cos ,tan 键的第二功能“sin-1,cos-1,tan-1”和
SHIFT 键.
2.具体操作步骤是:先按SHIFT 键,再按sin ,cos ,
tan 键之一,再依次输入三角函数值,最后按=键,
则屏幕上就会显示出结果.
探索新知
拓展:
(1)上面得出的结果是以“度”为单位的,再按°’”键
即可显示以“度、分、秒”为单位的结果.
(2)求角度的计算结果,如没有特别说明,一般精确到1″.
3.易错警示:注意由值求角必须保证按键顺序正确.
探索新知
例3 根据下列条件求锐角A 的度数:(结果精确到1′)
(1)sin A=0.732 1;(2)cos A=0.218 7;(3)tan A=3.527.
导引:利用sin ,cos ,tan 键的第二功能计算,即先按SHIFT键,再按sin或cos或tan键,然后输入三角函数值,最后按=键,即可显示结果.
探索新知
解:
(1)先按SHIFT sin 0.7321=键,显示:47.062 734 57,再按°’”键,即可显示47°3′45.84″,所以∠A≈47°4′.
(2)先按 SHIFT cos 0.2187=键,显示:77.367 310 78,再按°’”键,显示77°22′2.32″,所以∠A≈77°22′.
(3)先按 SHIFT tan 3.527=键,显示:74.170 530 81,再按°’”键,显示74°10′13.91″,所以∠A≈74°10′.
探索新知
总 结
由值求角,计算器显示的角度的单位是“度”,一般需要化为用“度、分、秒”表示的形式,用°’”键可实现两者间的转换.
典题精讲
已知α为锐角,且tan α=3.387,下列各值中与α 最接近的是( )
A.73°33′ B.73°27′ C.16°27′ D.16°21′
在△ABC 中,∠C=90°,BC=5,AB=13,用科学计算器求∠A 约等于( )
A.24°38′ B.65°22′ C.67°23′ D.22°37′
A
D
典题精讲
如图,有一滑梯AB,其水平宽度AC 为5.3 m,铅直高度BC 为2.8 m,则∠A的度数约为________(用科学计算器计算,结果精确到0.1°).
27.8
探索新知
3
知识点
用计算器探究三角函数的性质
三角函数值的大小有锐角的度数决定,与其在哪个直角三角形中无关,具体来说:
(1)tan A随着∠A的增大而增大,∠A越接近90°,tanA的值就增加得越快,tan A可以等于任何一个正数.
(2)sin A的值随着锐角A的增大而增大;cos A的值随着锐角A的增大而减小.
探索新知
例4 已知α,β 为锐角,且cos α 是方程2x2+5x-3=0的一个根,cos β≥cos α,试求α 的度数及β 的取值范围.
先求出方程2x2+5x-3=0的根,从而得到cos α 的值,再根据特殊角的三角函数值求出α 的度数,最后根据锐角三角函数的增减性确定β 的取值范围.
导引:
探索新知
解方程2x 2+5x-3=0,得x1=-3,x2=
∵0<cos α<1,且cos α 是方程2x 2+5x-3=0的一个根,
∴cos α=
∵cos 60°= ∴α=60°.
∵β 为锐角,cos β≥cos α,∴cos β≥cos 60°.
又∵锐角的余弦值随角的度数的增大而减小,
∴0°<β≤60°.
解:
探索新知
总 结
解方程,由特殊角的三角函数值可知α 的度数,再利用锐角与其余弦值的关系,通过比较得到β 的取值范围.
典题精讲
在Rt△ABC 中,∠C=90°,下列各式中正确的是 ( )
A.sin A=sin B B.tan A=tan B
C.sin A=cos B D.cos A=cos B
用计算器比较tan 25°,sin 27°,cos 26°的大小关系是( )
A.tan 25°
C
典题精讲
用计算器求sin 15°,sin 25°,sin 35°,sin 45°,sin 55°,sin 65°,sin 75°,sin 85°的值,研究sin α的值随锐角变化的规律,根据这个规律判断:
若
C.0°<α<60° D.60°<α<90°
A
学以致用
小试牛刀
1.计算sin245°+cos 30°·tan 60°,其结果是( )
A.2 B.1 C. D.
2.下列各式中正确的是( )
A.sin 60°=
B.cos 45°+sin 45°=
C.sin 60°=sin(2×30°)=2sin 30°
D.tan 60°+tan 30°=2
B
A
小试牛刀
3.用计算器求下列锐角三角函数值:
(1)sin 20°,cos 70°; sin 35°, cos 55°;sin15°32′,cos74°28′;
(2)tan 3° 8',tan 80° 25′43".
(1)sin 20°≈0.342 0,cos 70°≈0.342 0;
sin 35°≈0.573 6,cos 55°≈0.573 6;
sin 15°32′≈0.267 8,cos 74°28′≈0.267 8.
(2)tan 3°8′≈0.054 7,tan 80°25′43″≈5.930 4.
解:
小试牛刀
4.用计算器计算cos 44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
5.用计算器验证,下列等式正确的是( )
A.sin 18°24′+sin 35°36′=sin 54°
B.sin 65°54′-sin 35°54′=sin 30°
C.2sin 15°30′=sin 31°
D.sin 72°18′-sin 12°18′=sin 47°42′
B
D
小试牛刀
6.为了方便行人推车过某天桥,市政府在10 m高的天桥一侧修建了40 m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. 2ndF sin 0 · 2 5 =
B. sin 2ndF 0 · 2 5 =
C. sin 0 · 2 5 =
D. 2ndF cos 0 · 2 5 =
A
小试牛刀
7.(1)如图①②,锐角的正弦值和余弦值都随着锐角的变化而化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.
小试牛刀
(3)比较大小(在横线上填写“<”“>”或“=”):
若α=45°,则sin α________cos α;
若α<45°,则sin α________cos α;
若α>45°,则sin α________cos α.
(4)利用互为余角的两个角的正弦值和余弦值的关系,试比较下列正弦值和余弦值的大小:sin 10°,cos 30°,sin 50°,cos 70°.
(1)锐角的正弦值随角度的增大而增大,余弦值随角度的
增大而减小.
(2)sin 18°
<
=
>
小试牛刀
8.如图,一艘海轮在A点时测得灯塔C 在它的北偏东42°方向上,它沿正东方向航行80海里后到达B 处,此时灯塔C 在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C 的最短距离(结果精确到0.1);
(2)求海轮在B 处时与灯塔C 的距离(结果保留整数).
(参考数据:sin 55°≈0.819,cos 55°≈0.574,
tan 55°≈1.428,tan 42°≈0.900,
tan 35°≈0.700,tan 48°≈1.111)
小试牛刀
解:
(1)如图,过C 作AB的垂线,垂足为D,
根据题意可得:∠ACD=42°,∠BCD
=55°.设CD 的长为x 海里,
在Rt△ACD 中,tan 42°= ,则AD=x ·tan 42°海里,
在Rt△BCD 中,tan 55°= ,则BD=x ·tan 55°海里.
∵AB=80海里,∴AD+BD=80海里,
∴x ·tan 42°+x ·tan 55°=80,解得x≈34.4,
即海轮在航行过程中与灯塔C 的最短距离约是34.4海里.
(2)在Rt△BCD 中,cos 55°= ,
∴BC= ≈60(海里),
即海轮在B 处时与灯塔C 的距离约是60海里.
课堂小结
课堂小结
1.利用计算器可求锐角的三角函数值,按键顺序:先按
sin键或cos键或tan键,再按角度值,最后按=键,就
可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺序:
先按SHIFT键,再按sin键或cos键或tan键,然后输入
三角函数值,最后按=键,就可求出相应角度.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
