冀教版(新)九上-27.2 反比例函数的图象与性质 第三课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-27.2 反比例函数的图象与性质 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
27.2 反比例函数的图象与性质
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
反比例函数图像的位置及增减性由k 的符号决定,|k |决定图像上一点向两坐标轴所作垂线与两坐标轴围成的矩形面积,中考时常将反比例函数图像和性质与其他函数、几何图像综合在一起进行考查,是中考压轴题中一个重要的命题方向.
新课精讲
探索新知
1
题型
利用反比例函数解与图形旋转相关的问题
如图,△ABC 的顶点坐标为A(-2,3),B(-3,1),C (-1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C ′,点B ′,C ′分别是点B,C的对应点.求:
(1)过点B ′的反比例函数的表达式;
(2)线段CC ′的长.
探索新知
(1)由题易得点B 的对应点B ′的坐标为(1,3),
设过点B ′的反比例函数表达式为
∴k=3×1=3.
∴过点B ′的反比例函数表达式为
解:
探索新知
(2)连接OC,OC ′.
∵点C 的坐标为(-1,2),
∴OC=
∵△ABC 以坐标原点O 为旋转中心,顺时针旋转90°,得到
△A′B′C ′,点C ′是点C 的对应点,
∴OC ′=OC=5,∠COC ′=90°.
∴CC ′=
探索新知
2
利用反比例函数解与图形的轴对称相关的问题
题型
如图,一次函数y=x+b 的图像与反比例函数y=
(k 为常数,k≠0)的图像交于点A(-1,4)和点B(a,1).
(1)求反比例函数的表达式
和a,b 的值;
(2)若A,O 两点关于直线l对
称,请连接AO,并求出直线l
与线段AO 的交点坐标.
探索新知
(1)∵点A(-1,4)在反比例函数 (为常数,
k≠0)的图像上,
∴k=-1×4=-4.
∴反比例函数的表达式为
把点A(-1,4),B (a,1)的坐标分别代入y=x+b,
得
解得
解:
探索新知
(2)如图,设线段AO 与直线l相交于点M.
∵A,O 两点关于直线l对称,
∴点M 为线段OA 的中点.
∵点A(-1,4),O (0,0),
∴点M 的坐标为
即直线l与线段AO的交点坐标为
探索新知
3
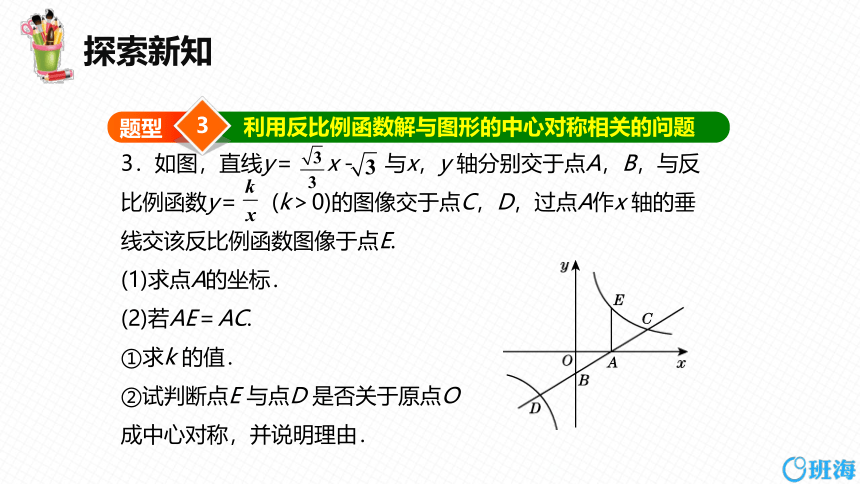
利用反比例函数解与图形的中心对称相关的问题
题型
3.如图,直线y= x- 与x,y 轴分别交于点A,B,与反比例函数y= (k>0)的图像交于点C,D,过点A作x 轴的垂线交该反比例函数图像于点E.
(1)求点A的坐标.
(2)若AE=AC.
①求k 的值.
②试判断点E 与点D 是否关于原点O
成中心对称,并说明理由.
探索新知
(1)当y=0时,得0= x- ,解得x=3.
∴点A 的坐标为(3,0).
解:
(2)①如图,过点C 作CF⊥x 轴于点F.
设AE=AC=t,易知点E 的坐标是(3,t ),
在Rt△AOB 中,
易知OB= ,OA=3,
∴AB=
∴AB=2OB. ∴∠OAB=30°.
∴∠CAF=30°.∴CF= t.
探索新知
∴
∴点C的坐标是
又∵点C与点E均在反比例函数 (k>0)的图像上,
∴
解得t1=0(舍去),t2=2 .
∴k=3t=6 .
探索新知
②点E 与点D 关于原点O 成中心对称.理由如下:
设点D的坐标是
则
解得x1=6(舍去),x2=-3.
∴点D 的坐标是(-3,-2 ).
又∵点E 的坐标为(3,2 ),
∴点E 与点D 关于原点O 成中心对称.
探索新知
4
利用反比例函数解与图形的平移相关的问题
4.如图,反比例函数y= 与一次函数y=ax+b 的图
像交于点A(2,2), B ( ,n).
(1)求这两个函数表达式;
(2)将一次函数y=ax+b 的图像沿y
轴向下平移m 个单位长度,使平
移后的图像与反比例函数y=
的图像有且只有一个交点,
求m 的值.
题型
探索新知
解:
(1)∵A(2,2)在反比例函数y= 的图像上,
∴k=4.
∴反比例函数的表达式为y=
又∵点B 在反比例函数y= 的图像上,
∴ n=4,解得n=8,
即点B 的坐标为
探索新知
由A(2,2),B 在一次函数y=ax+b 的
图像上,
得
解得
探索新知
(2)由(1)得,一次函数的表达式为y=-4x+10. 将直线y=-4x+10向下平移m 个单位长度得直线对应的函数表达式为y=-4x+10-m,
∵直线y=-4x+10-m与双曲线y= 有且只有一个交点,
令 -4x+10-m= ,得4x 2+(m-10)x+4=0,
∴Δ=(m-10)2-64=0,
解得m=2或m=18.
探索新知
5
利用反比例函数解与最值相关的问题
5.如图,已知点A(1,a)是反比例函数y=- 的图像
上一点,直线y=- x+ 与反比例函数y=-
的图像在第四象限的交点为点B.
(1)求直线AB 对应的函数表达式;
(2)动点P (x,0)在x 轴的正半轴上
运动,当线段PA与线段PB 的
长度之差达到最大时,求点P
的坐标.
题型
探索新知
解:
(1)将A(1,a)的坐标代入y=- 中,得a=-3,
∴A(1,-3).
∵B点是直线y=- x+ 与反比例函数
y=- 的图像在第四象限的交点,
由
∴点B 的坐标为(3,-1).
设直线AB 对应的函数表达式为y=kx+b,
探索新知
∴y=x-4.
(2)当P点为直线AB与x轴的交点时,线段PA与线段PB的长度之差最大.
∵直线AB 对应的函数表达式为y=x-4,
∴点P 的坐标为(4,0).
探索新知
6
利用反比例函数解与最值相关的问题
6. 如图,在平面直角坐标系中,直线y=2x与反比例函数y= 在第一象限内的图像交于点A(m,2).将直线y=2x 向下平移后与反比例函数在第一象限内的图像交于点P,
且△POA的面积为2.
求:(1)k 的值;
(2)平移后的直线对应的函
数表达式.
题型
探索新知
解:
(1)∵点A(m,2)在直线y=2x上,
∴2=2m.
∴m=1.
∴点A 的坐标为A(1,2).
又点A (1,2)在反比例函数y= 的图像上,
∴k=2.
探索新知
(2)如图,设平移后的直线与y 轴交于点B,连接AB,则
S△OAB=S△OAP=2.
过点A作y 轴的垂线AC,垂足为点C,
则AC=1.
∴OB·AC=2.
∴OB=4.
∴平移后的直线对应的函
数表达式为y=2x-4.
探索新知
7
题型
利用反比例函数解与一次函数、三角形面积综合的问题
如图,平行四边形ABCD 的两个顶点A,C 在反比例函数
(k≠0)图象上,点B,D 在x 轴上,且B,D 两点关
于原点对称,AD 交y 轴于P点.
(1)已知点A的坐标是(2,3),
求k 的值及C点的坐标;
(2)若△APO 的面积为2,求
点D 到直线AC 的距离.
探索新知
解:(1)∵点A 的坐标是(2,3),且点A在反比例函数
(k≠0)图象上,
∴ ∴k=6,
又易知点C 与点A 关于原点O 对称,
∴C 点的坐标为(-2,-3).
(2)∵△APO 的面积为2,点A 的坐标是(2,3),
∴2= ,解得OP=2,
∴点P 的坐标为(0,2).
探索新知
设过点P (0,2),点A(2,3)的直线对应的函数
表达式为y=ax+b,
∴ 解得
即直线PA对应函数的解析式为y= x+2.
将y=0代入y= x+2,得x=-4,
∴D 点的坐标为(-4,0).
∴OD=4,
探索新知
∵A(2,3),C (-2,-3),
∴AC=
设点D 到AC 的距离为m,
∵S△ACD=S△ODA+S△ODC,
∴
解得m= ,即点D 到直线AC 的距离是
学以致用
小试牛刀
1.如图,点A,B分别在x轴、y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA= ,反比例函数y= (k>0)的图像过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图像上,并说明理由.
小试牛刀
(1)证明:∵点A,B分别在x轴,y轴上,点D在第一象限内,DC⊥x轴于点C,∴∠AOB=∠DCA=90°.
在Rt△AOB和Rt△DCA中,
∴Rt△AOB≌Rt△DCA.
小试牛刀
(2)解:在Rt△ACD中,∵CD=2,DA= ,
∴OC=OA+AC=2+1=3.
∴D点坐标为(3,2).
∵点E为CD的中点,
∴点E的坐标为(3,1).
∴k=3×1=3.
小试牛刀
(3)解:点G在反比例函数的图像上.
理由如下:∵△BFG和△DCA关于某点成中心对称,∴△BFG≌△DCA.
∴FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°.
易知OB=AC=1,∴OF=OB+BF=1+2=3. ∴G点坐标为(1,3).∵1×3=3,∴点G(1,3)在反比例函数的图像上.
小试牛刀
2.如图,过反比例函数y= (x>0)的图像上一点A作x轴的平行线,交双曲线y= (x<0)于点B,过B作BC∥OA交双曲线y= (x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
小试牛刀
解:设点A的坐标为 ,由题易知四边形ABCO是平行四边形,
∴AB=OC=3.
∴点B的坐标为
∴(a-3) =-3.
∴a=2.
∴A点的坐标为(2,3),B点的坐标为(-1,3).
∵C点的坐标为(-3,0),
∴直线BC对应的函数表达式为
整理得x2+3x+2=0,解得x1=-1,x2=-2.
∴直线AD对应的函数表达式为 ∴OE=94.
小试牛刀
小试牛刀
3.如图,矩形OABC的顶点A,C的坐标分别是(4,0)和(0,2),反比例函数y= (x>0)的图像过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为________.
小试牛刀
4.如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的双曲线对应的函数表达式.
小试牛刀
解:(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形.
∵四边形OABC是矩形,
∴DA=DB.
∴四边形AEBD是菱形.
小试牛刀
(2)解:连接DE,交AB于F,
易知DE=OA=3.
∵四边形AEBD是菱形,
设所求反比例函数表达式为
把点E 的坐标代入得 ,解得 .
∴所求反比例函数表达式为 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.2 反比例函数的图象与性质
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
反比例函数图像的位置及增减性由k 的符号决定,|k |决定图像上一点向两坐标轴所作垂线与两坐标轴围成的矩形面积,中考时常将反比例函数图像和性质与其他函数、几何图像综合在一起进行考查,是中考压轴题中一个重要的命题方向.
新课精讲
探索新知
1
题型
利用反比例函数解与图形旋转相关的问题
如图,△ABC 的顶点坐标为A(-2,3),B(-3,1),C (-1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C ′,点B ′,C ′分别是点B,C的对应点.求:
(1)过点B ′的反比例函数的表达式;
(2)线段CC ′的长.
探索新知
(1)由题易得点B 的对应点B ′的坐标为(1,3),
设过点B ′的反比例函数表达式为
∴k=3×1=3.
∴过点B ′的反比例函数表达式为
解:
探索新知
(2)连接OC,OC ′.
∵点C 的坐标为(-1,2),
∴OC=
∵△ABC 以坐标原点O 为旋转中心,顺时针旋转90°,得到
△A′B′C ′,点C ′是点C 的对应点,
∴OC ′=OC=5,∠COC ′=90°.
∴CC ′=
探索新知
2
利用反比例函数解与图形的轴对称相关的问题
题型
如图,一次函数y=x+b 的图像与反比例函数y=
(k 为常数,k≠0)的图像交于点A(-1,4)和点B(a,1).
(1)求反比例函数的表达式
和a,b 的值;
(2)若A,O 两点关于直线l对
称,请连接AO,并求出直线l
与线段AO 的交点坐标.
探索新知
(1)∵点A(-1,4)在反比例函数 (为常数,
k≠0)的图像上,
∴k=-1×4=-4.
∴反比例函数的表达式为
把点A(-1,4),B (a,1)的坐标分别代入y=x+b,
得
解得
解:
探索新知
(2)如图,设线段AO 与直线l相交于点M.
∵A,O 两点关于直线l对称,
∴点M 为线段OA 的中点.
∵点A(-1,4),O (0,0),
∴点M 的坐标为
即直线l与线段AO的交点坐标为
探索新知
3
利用反比例函数解与图形的中心对称相关的问题
题型
3.如图,直线y= x- 与x,y 轴分别交于点A,B,与反比例函数y= (k>0)的图像交于点C,D,过点A作x 轴的垂线交该反比例函数图像于点E.
(1)求点A的坐标.
(2)若AE=AC.
①求k 的值.
②试判断点E 与点D 是否关于原点O
成中心对称,并说明理由.
探索新知
(1)当y=0时,得0= x- ,解得x=3.
∴点A 的坐标为(3,0).
解:
(2)①如图,过点C 作CF⊥x 轴于点F.
设AE=AC=t,易知点E 的坐标是(3,t ),
在Rt△AOB 中,
易知OB= ,OA=3,
∴AB=
∴AB=2OB. ∴∠OAB=30°.
∴∠CAF=30°.∴CF= t.
探索新知
∴
∴点C的坐标是
又∵点C与点E均在反比例函数 (k>0)的图像上,
∴
解得t1=0(舍去),t2=2 .
∴k=3t=6 .
探索新知
②点E 与点D 关于原点O 成中心对称.理由如下:
设点D的坐标是
则
解得x1=6(舍去),x2=-3.
∴点D 的坐标是(-3,-2 ).
又∵点E 的坐标为(3,2 ),
∴点E 与点D 关于原点O 成中心对称.
探索新知
4
利用反比例函数解与图形的平移相关的问题
4.如图,反比例函数y= 与一次函数y=ax+b 的图
像交于点A(2,2), B ( ,n).
(1)求这两个函数表达式;
(2)将一次函数y=ax+b 的图像沿y
轴向下平移m 个单位长度,使平
移后的图像与反比例函数y=
的图像有且只有一个交点,
求m 的值.
题型
探索新知
解:
(1)∵A(2,2)在反比例函数y= 的图像上,
∴k=4.
∴反比例函数的表达式为y=
又∵点B 在反比例函数y= 的图像上,
∴ n=4,解得n=8,
即点B 的坐标为
探索新知
由A(2,2),B 在一次函数y=ax+b 的
图像上,
得
解得
探索新知
(2)由(1)得,一次函数的表达式为y=-4x+10. 将直线y=-4x+10向下平移m 个单位长度得直线对应的函数表达式为y=-4x+10-m,
∵直线y=-4x+10-m与双曲线y= 有且只有一个交点,
令 -4x+10-m= ,得4x 2+(m-10)x+4=0,
∴Δ=(m-10)2-64=0,
解得m=2或m=18.
探索新知
5
利用反比例函数解与最值相关的问题
5.如图,已知点A(1,a)是反比例函数y=- 的图像
上一点,直线y=- x+ 与反比例函数y=-
的图像在第四象限的交点为点B.
(1)求直线AB 对应的函数表达式;
(2)动点P (x,0)在x 轴的正半轴上
运动,当线段PA与线段PB 的
长度之差达到最大时,求点P
的坐标.
题型
探索新知
解:
(1)将A(1,a)的坐标代入y=- 中,得a=-3,
∴A(1,-3).
∵B点是直线y=- x+ 与反比例函数
y=- 的图像在第四象限的交点,
由
∴点B 的坐标为(3,-1).
设直线AB 对应的函数表达式为y=kx+b,
探索新知
∴y=x-4.
(2)当P点为直线AB与x轴的交点时,线段PA与线段PB的长度之差最大.
∵直线AB 对应的函数表达式为y=x-4,
∴点P 的坐标为(4,0).
探索新知
6
利用反比例函数解与最值相关的问题
6. 如图,在平面直角坐标系中,直线y=2x与反比例函数y= 在第一象限内的图像交于点A(m,2).将直线y=2x 向下平移后与反比例函数在第一象限内的图像交于点P,
且△POA的面积为2.
求:(1)k 的值;
(2)平移后的直线对应的函
数表达式.
题型
探索新知
解:
(1)∵点A(m,2)在直线y=2x上,
∴2=2m.
∴m=1.
∴点A 的坐标为A(1,2).
又点A (1,2)在反比例函数y= 的图像上,
∴k=2.
探索新知
(2)如图,设平移后的直线与y 轴交于点B,连接AB,则
S△OAB=S△OAP=2.
过点A作y 轴的垂线AC,垂足为点C,
则AC=1.
∴OB·AC=2.
∴OB=4.
∴平移后的直线对应的函
数表达式为y=2x-4.
探索新知
7
题型
利用反比例函数解与一次函数、三角形面积综合的问题
如图,平行四边形ABCD 的两个顶点A,C 在反比例函数
(k≠0)图象上,点B,D 在x 轴上,且B,D 两点关
于原点对称,AD 交y 轴于P点.
(1)已知点A的坐标是(2,3),
求k 的值及C点的坐标;
(2)若△APO 的面积为2,求
点D 到直线AC 的距离.
探索新知
解:(1)∵点A 的坐标是(2,3),且点A在反比例函数
(k≠0)图象上,
∴ ∴k=6,
又易知点C 与点A 关于原点O 对称,
∴C 点的坐标为(-2,-3).
(2)∵△APO 的面积为2,点A 的坐标是(2,3),
∴2= ,解得OP=2,
∴点P 的坐标为(0,2).
探索新知
设过点P (0,2),点A(2,3)的直线对应的函数
表达式为y=ax+b,
∴ 解得
即直线PA对应函数的解析式为y= x+2.
将y=0代入y= x+2,得x=-4,
∴D 点的坐标为(-4,0).
∴OD=4,
探索新知
∵A(2,3),C (-2,-3),
∴AC=
设点D 到AC 的距离为m,
∵S△ACD=S△ODA+S△ODC,
∴
解得m= ,即点D 到直线AC 的距离是
学以致用
小试牛刀
1.如图,点A,B分别在x轴、y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA= ,反比例函数y= (k>0)的图像过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图像上,并说明理由.
小试牛刀
(1)证明:∵点A,B分别在x轴,y轴上,点D在第一象限内,DC⊥x轴于点C,∴∠AOB=∠DCA=90°.
在Rt△AOB和Rt△DCA中,
∴Rt△AOB≌Rt△DCA.
小试牛刀
(2)解:在Rt△ACD中,∵CD=2,DA= ,
∴OC=OA+AC=2+1=3.
∴D点坐标为(3,2).
∵点E为CD的中点,
∴点E的坐标为(3,1).
∴k=3×1=3.
小试牛刀
(3)解:点G在反比例函数的图像上.
理由如下:∵△BFG和△DCA关于某点成中心对称,∴△BFG≌△DCA.
∴FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°.
易知OB=AC=1,∴OF=OB+BF=1+2=3. ∴G点坐标为(1,3).∵1×3=3,∴点G(1,3)在反比例函数的图像上.
小试牛刀
2.如图,过反比例函数y= (x>0)的图像上一点A作x轴的平行线,交双曲线y= (x<0)于点B,过B作BC∥OA交双曲线y= (x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
小试牛刀
解:设点A的坐标为 ,由题易知四边形ABCO是平行四边形,
∴AB=OC=3.
∴点B的坐标为
∴(a-3) =-3.
∴a=2.
∴A点的坐标为(2,3),B点的坐标为(-1,3).
∵C点的坐标为(-3,0),
∴直线BC对应的函数表达式为
整理得x2+3x+2=0,解得x1=-1,x2=-2.
∴直线AD对应的函数表达式为 ∴OE=94.
小试牛刀
小试牛刀
3.如图,矩形OABC的顶点A,C的坐标分别是(4,0)和(0,2),反比例函数y= (x>0)的图像过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为________.
小试牛刀
4.如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的双曲线对应的函数表达式.
小试牛刀
解:(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形.
∵四边形OABC是矩形,
∴DA=DB.
∴四边形AEBD是菱形.
小试牛刀
(2)解:连接DE,交AB于F,
易知DE=OA=3.
∵四边形AEBD是菱形,
设所求反比例函数表达式为
把点E 的坐标代入得 ,解得 .
∴所求反比例函数表达式为 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
