冀教版(新)九上-28.1 圆的概念及性质【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.1 圆的概念及性质【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览











文档简介
(共40张PPT)
28.1 圆的概念及性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆的定义
在实际生活中,电动自行车的车轮、皮带传动轮、茶几面和管道的横截面等,都给我们一种圆的形象 .
电动车车轮
皮带传动轮
茶几面
管道的横截面
探索新知
思考:
小惠与小亮合作,按下面的方法画圆 .
首先,小惠把绳子的一端固定在
操场上的某一点O处,小亮在绳子的另
一端拴上一小段竹签,然后,小亮将
绳子拉紧,再绕点O转一圈,竹签划出
的痕迹就是圆 .
观察小惠与小亮画圆的过程,你认为圆上任意一点到圆心的距离相等吗?
探索新知
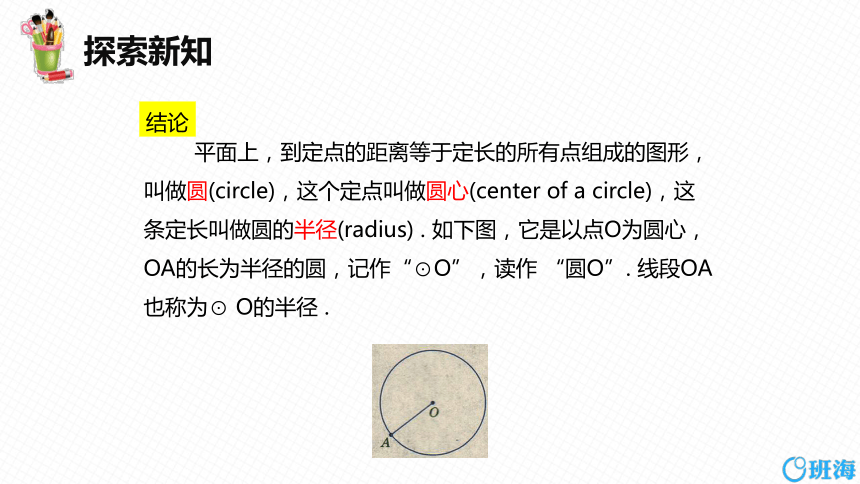
结论
平面上,到定点的距离等于定长的所有点组成的图形,叫做圆(circle),这个定点叫做圆心(center of a circle),这条定长叫做圆的半径(radius) . 如下图,它是以点O为圆心,OA的长为半径的圆,记作“⊙O”,读作 “圆O”. 线段OA也称为⊙ O的半径 .
探索新知
(1)确定一个圆需要两个要素,一是圆心,二是半径.圆心定其位置,半径定其大小.
(2)圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
(3)“圆上的点”指圆周上的点.
探索新知
下列说法中,错误的有( )
①经过点P的圆有无数个;②以点P为圆心的圆有无数个;③半径为3 cm且经过点P的圆有无数个;④以点P为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
例1
导引:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知①②正确;③半径确定,但圆心不确定,仍有无数个圆;④圆心和半径都确定的圆有且只有一个(唯一) .
A
探索新知
总 结
(1)确定圆的条件即圆心和半径,两者缺一不可;(2)“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上;(3)圆将平面划分为三部分:圆上、圆内、圆外.
典题精讲
1.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
D
典题精讲
2 . 矩形ABCD的对角线AC,BD相交于点O . 求证:A,B,C,D四个
点在以点O为圆心的同一个圆上 .
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,
AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的
圆上.(如图)
探索新知
2
知识点
圆的对称性
圆是轴对称图形,过圆心的每一条直线都是它的对称轴.圆也是中心对称图形,圆心是它的对称中心.
探索新知
1.圆是轴对称图形,过圆心的每一条直线都是它的对称轴.
(1)圆的对称轴有无数条;
(2)不能说“圆的对称轴是直径”,而应该说“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”.
2.圆是中心对称图形,圆心是它的对称中心.不仅如此,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合,即圆还具备旋转不变性.
探索新知
例2 如图所示,在⊙O中,将△AOB绕圆心O顺时针旋转150°,得
到△COD,指出图中相等的量.
导引:题中涉及的量有:弧、角、线段,按圆的旋转不变性这一规律找相等的量.
解:相等的弧有:
相等的角有:∠AOB=∠COD,∠AOC=∠BOD,
∠A=∠B=∠C=∠D;
相等的线段有:AB=CD,OA=OB=OC=OD .
探索新知
圆既是轴对称图形又是中心对称图形,而且绕圆心旋转任何一个角度都能与原图形重合,即圆具有旋转不变性.
总 结
1 下列图形中,对称轴条数最多的是( )
A.线段 B.正方形
C.正三角形 D.圆
典题精讲
在线段、平行四边形、矩形、等腰三角形、圆这几个图形中,
既是轴对称图形又是中心对称图形的有( )
A.2个 B.3个 C.4个 D.5个
D
B
典题精讲
3 下列图案中,是轴对称图形但不是中心对称图形的是( )
A
探索新知
3
知识点
与圆有关的概念
实际上,圆绕圆心旋转任意角度后都与自身重合 .
为进一步认识圆的有关性质,我们先了解关于圆的一些概念 .
圆上任意两点间的线段叫做这个圆的一条弦(chord) . 过圆心的弦叫做这个圆的直径(diameter) .
圆上任意两点间的部分叫做圆弧(circular arc),简称弧 . 圆的直径将这个圆分成能够完全重合的两条弧,这样的一条弧叫做半圆(semicircle) .
探索新知
大于半圆的弧叫做优弧(major arc),小于半圆的弧叫做劣弧(minorarc) .
如图,点A,B,C,D在⊙O上. 线段
AB为⊙O的一条弦,AC为⊙O的直径 . 直
径AC所分的两个半圆分别为半圆ADC和半圆ABC . 以AB为端点的弧有两条,其中劣弧用 来表示,读作“弧AB”,优弧用 来表示,读作“弧ADB”.
能够完全重合的两个圆叫做等圆.能够完全重合的两条弧叫做等弧 .
探索新知
例3 [易错题] 以下命题:①半圆是弧,但弧不一定是半圆;②过圆上任意一点只能作一条弦,且这条弦是直径;③弦是直径;④直径是圆中最长的弦;⑤直径不是弦;⑥优弧大于劣弧; ⑦以O为圆心可以画无数个圆 . 正确的个数为( )
A.1 B.2 C.3 D.4
导引:①半圆是弧的一种,弧可以分为劣弧、半圆、优弧三种,故正确;②过圆上任意一点可以作无数条弦,故错误;③直径是过圆心的特殊弦,但弦不一定是直径,故错误;④圆有无数条弦,过圆心的弦最长,即直径是圆中最长的弦,故正确;⑤直径是圆中最长的弦,故错误;⑥在同圆或等圆中,优弧大于劣弧,故错误;⑦以一个点为圆心,若不指明半径,可画出无数个大小不等的同心圆,故正确 .
C
探索新知
在圆的有关概念中有两个误区:
一是“半圆”和“弧”这两个概念之间的误区,半圆属于弧;
二是“弦”和“直径”之间的误区,直径是最长的弦.
总 结
典题精讲
如图所示 ,已知⊙O上有A,B,C三个点,以其中两个点为端
点的弧共有___条.
2 下列说法中,错误的是( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能相等
B
6
典题精讲
3 下列说法中,正确的是( )
①弦是直径; ②半圆是弧; ③过圆心的线段是直径;
④半圆是最长的弧; ⑤直径是圆中最长的弦.
A.②③ B.③⑤
C.④⑤ D.②⑤
D
探索新知
4
知识点
同圆的半径相等
(1)圆上各点到定点(圆心O)的距离都等于定长
(半径r),即同圆的半径相等.
(2)到定点O的距离等于定长r的点都在同一个
圆上,即到圆心的距离等于半径的点在圆上.
探索新知
例4 如图所示,BD,CE是△ABC的高.求证:E,
B,C,D四点在同一个圆上.
导引:要证E,B,C,D四点在同一个圆上,即需找出一个点,使这个点到E,B,C,D的距离相等,联想BC的中点F到B,C的距离相等,因此连接DF,EF,需证DF=EF= BC,利用直角三角形的性质易证.
探索新知
证明:如图所示,取BC的中点F,连接DF,EF .
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF= BC=BF=CF .
∴E,B,C,D四点在以F点为圆心, BC为
半径的圆上 .
已知,如图,OA,OB为⊙O的半径,C,D分别为OA,OB的两点,且AC=BD,求证:AD=BC .
典题精讲
导引:要证AD=BC,需证其所在的三角形全等,即需证△ADO≌△BCO .
证明:∵OA,OB是半径,∴OA=OB .
又∵AC=BD,∴OC=OD .
在△ADO和△BCO中,
∴△ADO≌△BCO . ∴AD=BC .
典题精讲
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B
是( )
A.100° B.72° C.64° D.36°
C
学以致用
小试牛刀
1.圆的形成定义:在一个平面内,线段绕它固定的一个端点旋转
________,另一个端点所形成的图形叫做圆.
2.圆的集合定义:圆心为O、半径为r的圆可以看成是所有到定点O
的距离等于________的点的集合.
一周
定长r
3.若圆的半径为3,则弦AB的长度的取值范围是______________.
0<AB≤6
小试牛刀
4.如图,在⊙O中,点A,O,D以及点B,O,C分别在一条直线
上,图中弦的条数是( )
A.2
B.3
C.5
D.6
B
小试牛刀
5.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;
②圆的任意一条弦把圆分成优弧和劣弧两部分;
③长度相等的弧是等弧;
④半径相等的圆是等圆;
⑤直径是圆中最长的弦.
A.2个 B.3个 C.4个 D.5个
A
小试牛刀
6.如图,AB是⊙O的直径,点D,C在⊙O上,AD//OC,∠DAB=60°,
连接AC,则∠DAC等于( )
A. 15° B. 30°
C. 45° D. 60°
B
小试牛刀
7. 如图,点A,B,C在⊙O上,点O在线段AC上,点D在线段AB上,
下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
小试牛刀
8 . 已知:如图,OA,OB为⊙O的半径,C,D分别为OA,
OB的中点.求证:AD=BC .
证明:∵OA,OB为⊙O的半径,
∴OA=OB.
∵C,D分别为OA,OB的中点, ∴OC=OD.
在△AOD和△BOC中,
∵OA=OB,∠O=∠O,OD=OC,
∴△AOD≌△BOC(SAS),∴AD=BC.
课堂小结
课堂小结
理解圆的定义要注意两层含义:
(1)圆上各点到圆心的距离都相等.在圆所在的平面内,到圆心距离等于半径的点必定在圆上;
(2)当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的运动轨迹就是一个圆.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.1 圆的概念及性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆的定义
在实际生活中,电动自行车的车轮、皮带传动轮、茶几面和管道的横截面等,都给我们一种圆的形象 .
电动车车轮
皮带传动轮
茶几面
管道的横截面
探索新知
思考:
小惠与小亮合作,按下面的方法画圆 .
首先,小惠把绳子的一端固定在
操场上的某一点O处,小亮在绳子的另
一端拴上一小段竹签,然后,小亮将
绳子拉紧,再绕点O转一圈,竹签划出
的痕迹就是圆 .
观察小惠与小亮画圆的过程,你认为圆上任意一点到圆心的距离相等吗?
探索新知
结论
平面上,到定点的距离等于定长的所有点组成的图形,叫做圆(circle),这个定点叫做圆心(center of a circle),这条定长叫做圆的半径(radius) . 如下图,它是以点O为圆心,OA的长为半径的圆,记作“⊙O”,读作 “圆O”. 线段OA也称为⊙ O的半径 .
探索新知
(1)确定一个圆需要两个要素,一是圆心,二是半径.圆心定其位置,半径定其大小.
(2)圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
(3)“圆上的点”指圆周上的点.
探索新知
下列说法中,错误的有( )
①经过点P的圆有无数个;②以点P为圆心的圆有无数个;③半径为3 cm且经过点P的圆有无数个;④以点P为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
例1
导引:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知①②正确;③半径确定,但圆心不确定,仍有无数个圆;④圆心和半径都确定的圆有且只有一个(唯一) .
A
探索新知
总 结
(1)确定圆的条件即圆心和半径,两者缺一不可;(2)“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上;(3)圆将平面划分为三部分:圆上、圆内、圆外.
典题精讲
1.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
D
典题精讲
2 . 矩形ABCD的对角线AC,BD相交于点O . 求证:A,B,C,D四个
点在以点O为圆心的同一个圆上 .
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,
AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的
圆上.(如图)
探索新知
2
知识点
圆的对称性
圆是轴对称图形,过圆心的每一条直线都是它的对称轴.圆也是中心对称图形,圆心是它的对称中心.
探索新知
1.圆是轴对称图形,过圆心的每一条直线都是它的对称轴.
(1)圆的对称轴有无数条;
(2)不能说“圆的对称轴是直径”,而应该说“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”.
2.圆是中心对称图形,圆心是它的对称中心.不仅如此,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合,即圆还具备旋转不变性.
探索新知
例2 如图所示,在⊙O中,将△AOB绕圆心O顺时针旋转150°,得
到△COD,指出图中相等的量.
导引:题中涉及的量有:弧、角、线段,按圆的旋转不变性这一规律找相等的量.
解:相等的弧有:
相等的角有:∠AOB=∠COD,∠AOC=∠BOD,
∠A=∠B=∠C=∠D;
相等的线段有:AB=CD,OA=OB=OC=OD .
探索新知
圆既是轴对称图形又是中心对称图形,而且绕圆心旋转任何一个角度都能与原图形重合,即圆具有旋转不变性.
总 结
1 下列图形中,对称轴条数最多的是( )
A.线段 B.正方形
C.正三角形 D.圆
典题精讲
在线段、平行四边形、矩形、等腰三角形、圆这几个图形中,
既是轴对称图形又是中心对称图形的有( )
A.2个 B.3个 C.4个 D.5个
D
B
典题精讲
3 下列图案中,是轴对称图形但不是中心对称图形的是( )
A
探索新知
3
知识点
与圆有关的概念
实际上,圆绕圆心旋转任意角度后都与自身重合 .
为进一步认识圆的有关性质,我们先了解关于圆的一些概念 .
圆上任意两点间的线段叫做这个圆的一条弦(chord) . 过圆心的弦叫做这个圆的直径(diameter) .
圆上任意两点间的部分叫做圆弧(circular arc),简称弧 . 圆的直径将这个圆分成能够完全重合的两条弧,这样的一条弧叫做半圆(semicircle) .
探索新知
大于半圆的弧叫做优弧(major arc),小于半圆的弧叫做劣弧(minorarc) .
如图,点A,B,C,D在⊙O上. 线段
AB为⊙O的一条弦,AC为⊙O的直径 . 直
径AC所分的两个半圆分别为半圆ADC和半圆ABC . 以AB为端点的弧有两条,其中劣弧用 来表示,读作“弧AB”,优弧用 来表示,读作“弧ADB”.
能够完全重合的两个圆叫做等圆.能够完全重合的两条弧叫做等弧 .
探索新知
例3 [易错题] 以下命题:①半圆是弧,但弧不一定是半圆;②过圆上任意一点只能作一条弦,且这条弦是直径;③弦是直径;④直径是圆中最长的弦;⑤直径不是弦;⑥优弧大于劣弧; ⑦以O为圆心可以画无数个圆 . 正确的个数为( )
A.1 B.2 C.3 D.4
导引:①半圆是弧的一种,弧可以分为劣弧、半圆、优弧三种,故正确;②过圆上任意一点可以作无数条弦,故错误;③直径是过圆心的特殊弦,但弦不一定是直径,故错误;④圆有无数条弦,过圆心的弦最长,即直径是圆中最长的弦,故正确;⑤直径是圆中最长的弦,故错误;⑥在同圆或等圆中,优弧大于劣弧,故错误;⑦以一个点为圆心,若不指明半径,可画出无数个大小不等的同心圆,故正确 .
C
探索新知
在圆的有关概念中有两个误区:
一是“半圆”和“弧”这两个概念之间的误区,半圆属于弧;
二是“弦”和“直径”之间的误区,直径是最长的弦.
总 结
典题精讲
如图所示 ,已知⊙O上有A,B,C三个点,以其中两个点为端
点的弧共有___条.
2 下列说法中,错误的是( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能相等
B
6
典题精讲
3 下列说法中,正确的是( )
①弦是直径; ②半圆是弧; ③过圆心的线段是直径;
④半圆是最长的弧; ⑤直径是圆中最长的弦.
A.②③ B.③⑤
C.④⑤ D.②⑤
D
探索新知
4
知识点
同圆的半径相等
(1)圆上各点到定点(圆心O)的距离都等于定长
(半径r),即同圆的半径相等.
(2)到定点O的距离等于定长r的点都在同一个
圆上,即到圆心的距离等于半径的点在圆上.
探索新知
例4 如图所示,BD,CE是△ABC的高.求证:E,
B,C,D四点在同一个圆上.
导引:要证E,B,C,D四点在同一个圆上,即需找出一个点,使这个点到E,B,C,D的距离相等,联想BC的中点F到B,C的距离相等,因此连接DF,EF,需证DF=EF= BC,利用直角三角形的性质易证.
探索新知
证明:如图所示,取BC的中点F,连接DF,EF .
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF= BC=BF=CF .
∴E,B,C,D四点在以F点为圆心, BC为
半径的圆上 .
已知,如图,OA,OB为⊙O的半径,C,D分别为OA,OB的两点,且AC=BD,求证:AD=BC .
典题精讲
导引:要证AD=BC,需证其所在的三角形全等,即需证△ADO≌△BCO .
证明:∵OA,OB是半径,∴OA=OB .
又∵AC=BD,∴OC=OD .
在△ADO和△BCO中,
∴△ADO≌△BCO . ∴AD=BC .
典题精讲
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B
是( )
A.100° B.72° C.64° D.36°
C
学以致用
小试牛刀
1.圆的形成定义:在一个平面内,线段绕它固定的一个端点旋转
________,另一个端点所形成的图形叫做圆.
2.圆的集合定义:圆心为O、半径为r的圆可以看成是所有到定点O
的距离等于________的点的集合.
一周
定长r
3.若圆的半径为3,则弦AB的长度的取值范围是______________.
0<AB≤6
小试牛刀
4.如图,在⊙O中,点A,O,D以及点B,O,C分别在一条直线
上,图中弦的条数是( )
A.2
B.3
C.5
D.6
B
小试牛刀
5.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;
②圆的任意一条弦把圆分成优弧和劣弧两部分;
③长度相等的弧是等弧;
④半径相等的圆是等圆;
⑤直径是圆中最长的弦.
A.2个 B.3个 C.4个 D.5个
A
小试牛刀
6.如图,AB是⊙O的直径,点D,C在⊙O上,AD//OC,∠DAB=60°,
连接AC,则∠DAC等于( )
A. 15° B. 30°
C. 45° D. 60°
B
小试牛刀
7. 如图,点A,B,C在⊙O上,点O在线段AC上,点D在线段AB上,
下列说法正确的是( )
A.线段AB,AC,CD,OB都是弦
B.与线段OB相等的线段有OA,OC,CD
C.图中的优弧有2条
D.AC是弦,AC又是⊙O的直径,所以弦是直径
C
小试牛刀
8 . 已知:如图,OA,OB为⊙O的半径,C,D分别为OA,
OB的中点.求证:AD=BC .
证明:∵OA,OB为⊙O的半径,
∴OA=OB.
∵C,D分别为OA,OB的中点, ∴OC=OD.
在△AOD和△BOC中,
∵OA=OB,∠O=∠O,OD=OC,
∴△AOD≌△BOC(SAS),∴AD=BC.
课堂小结
课堂小结
理解圆的定义要注意两层含义:
(1)圆上各点到圆心的距离都相等.在圆所在的平面内,到圆心距离等于半径的点必定在圆上;
(2)当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的运动轨迹就是一个圆.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
