冀教版(新)九上-28.3 圆心角与圆周角 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)九上-28.3 圆心角与圆周角 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:53:47 | ||
图片预览







文档简介
(共30张PPT)
28.3 圆心角与圆周角
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
什么是圆心角?它具有哪些性质?
新课精讲
探索新知
1
知识点
圆周角的定义
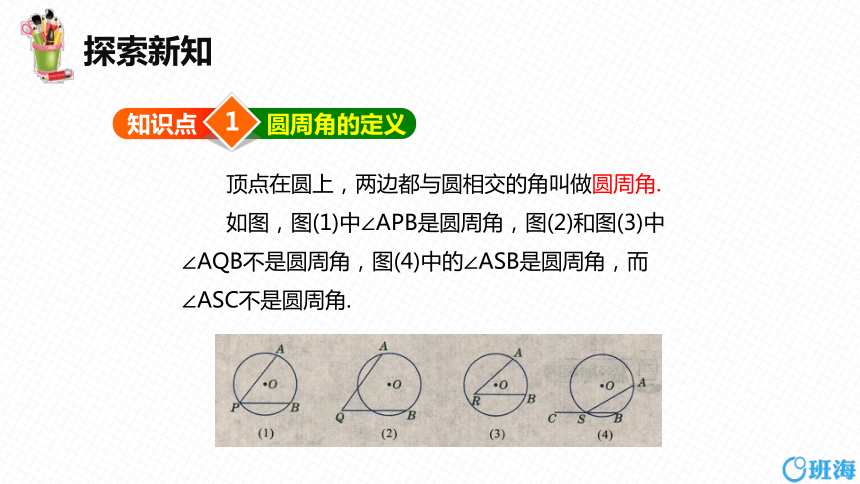
顶点在圆上,两边都与圆相交的角叫做圆周角.
如图,图(1)中∠APB是圆周角,图(2)和图(3)中 ∠AQB不是圆周角,图(4)中的∠ASB是圆周角,而∠ASC不是圆周角.
探索新知
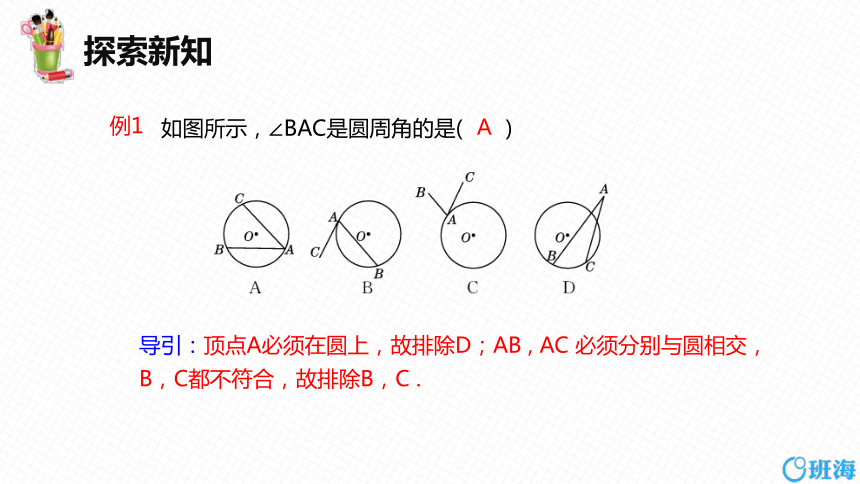
如图所示,∠BAC是圆周角的是( )
例1
导引:顶点A必须在圆上,故排除D;AB , AC 必须分别与圆相交,B,C都不符合,故排除B,C .
A
探索新知
总 结
本题运用定义法和排除法,判断一个角是不是圆周角,必须抓住圆周角定义中的两个特征:
(1)角的顶点在圆周上;(2)角的两边都与圆相交.
典题精讲
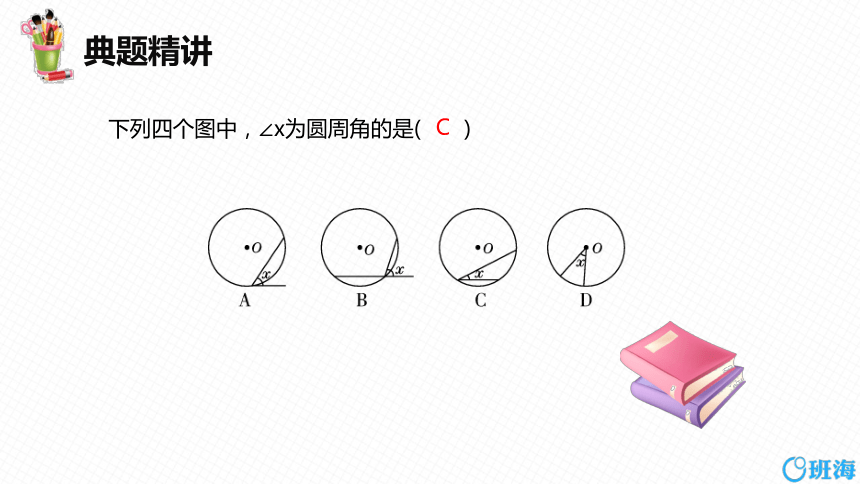
下列四个图中,∠x为圆周角的是( )
C
探索新知
2
知识点
圆周角和圆心角的关系
如图,∠AOB和∠APB分别是 所对的圆心角和圆周角 .
(1)当点P在圆上按顺时针方向移动时(点P与点B不
重合),按照圆心O和圆周角的位置关系,可以分为几
种不同的情形?说出你的判断并画出相应的图形 .
(2)当圆心O落在∠APB的一条边上时,∠AOB与∠APB具有怎样的大小关系?说明理由 .
(3)当圆心O在的内部和外部时,(2)中的结论还成立吗?和同学进行交流 .
探索新知
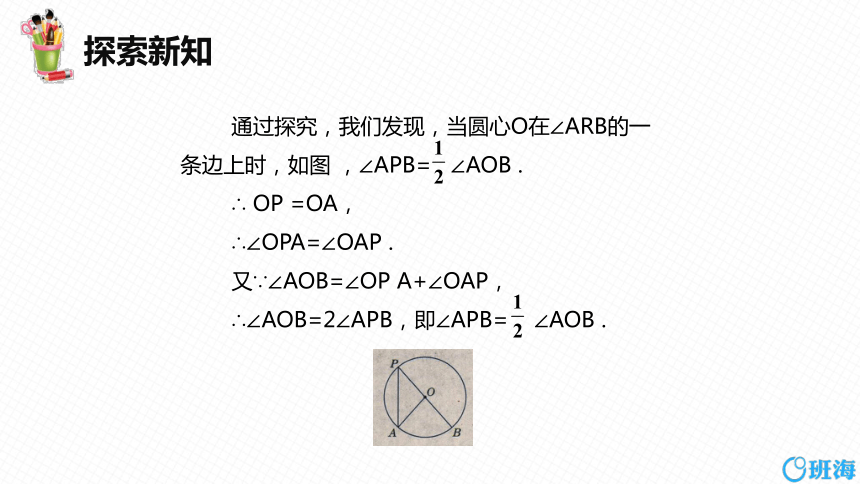
通过探究,我们发现,当圆心O在∠ARB的一条边上时,如图 ,∠APB= ∠AOB .
∴ OP =OA,
∴∠OPA=∠OAP .
又∵∠AOB=∠OP A+∠OAP,
∴∠AOB=2∠APB,即∠APB= ∠AOB .
探索新知
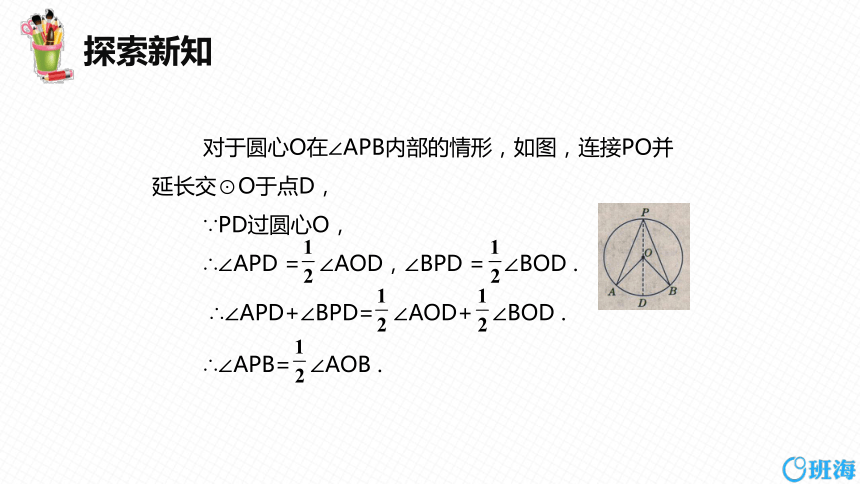
对于圆心O在∠APB内部的情形,如图,连接PO并延长交⊙O于点D,
∵PD过圆心O,
∴∠APD = ∠AOD,∠BPD = ∠BOD .
∴∠APD+∠BPD= ∠AOD+ ∠BOD .
∴∠APB= ∠AOB .
探索新知
如图,对于圆心O在圆周角∠APB外部的情形,证明∠APB= ∠AOB .
做一做
结论
圆上一条弧所对的圆周角等于它所对的圆心角的一半 .
探索新知
例2 如图 ,点 A,B,C 均在⊙O 上,∠OAB = 46°. 求
∠ACB的度数 .
解:如图,连接OB .
∵OA=OB,
∴∠OAB=∠OBA .
∵∠OAB =46°,
∴∠AOB= 180°-2∠OAB=180°-2×46°= 88°.
∴∠ACB= ∠AOB= 44°.
探索新知
在同一个圆中,根据相等的弧所对的圆心角相等和圆上一条弧所对的圆周角等于它所对的圆心角的一半可知,若两条弧相等,则其中一条弧所对的圆心角等于另一条弧所对的圆周角的2倍.
总 结
典题精讲
1 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
A.60°
B.48°
C.30°
D.24°
D
典题精讲
将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB=______.
如图,BD是⊙O的直径,点A,C在⊙O上, ,∠AOB=60°,则∠BDC的度数是( )
A.60° B.45° C.35° D.30°
(第2题)
(第3题)
25°
D
探索新知
3
知识点
同弧或等弧与所对圆周角的关系
结合弧、弦、圆心角之间的关系定理和圆周角定理的推论可知:在同圆或等圆中,相等的圆周角所对的弧相等,所对的弦也相等,进而相等的弧所对的圆心角也相等.即在同圆或等圆中,圆周角、圆心角、弧、弦这四个量中有一组量相等,则可推出其他三组量相等,也称之为“四量关系定理”.
探索新知
例3 如图,在⊙O中, ,∠BAC=50°,则∠AEC的度数
为( )
A.65° B.75° C.50° D.55°
A
导引:由 ,可知∠ABC=∠ACB,已知
∠BAC=50°,故根据三角形内角和定理,可求出
∠ABC的度数,再根据“同弧所对的圆周角相等”,可得结果.
∵ ,∴∠ABC=∠ACB .
∵∠BAC=50°,∴∠ABC= ×(180°-50°)=65°.
∴∠AEC=∠ABC=65°,故选A .
探索新知
在一个圆中求一个圆周角的度数,可以从三个方面转化:
(1)转化为求该圆周角所对的弧所对的圆心角的度数;
(2)转化为求该圆周角所对的弧所对的其他圆周角的度数;
(3)转化为求与该圆周角所对的弧相等的弧所对的圆心角或圆周角的度数.
总 结
典题精讲
如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是 上一点,则∠APB的度数为( )
A.45° B.30° C.75° D.60°
D
典题精讲
如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=
75°,则∠B的度数是( )
A.15° B.25°
C.30° D.75°
如图,在⊙O中, ,∠AOB=40°,则∠ADC的度数是( )
A.40° B.30°
C.20° D.15°
C
C
学以致用
小试牛刀
如图所示,图中的圆周角共有______个,其中AB所对的圆周角是
___________,CD所对的圆周角是__________.
⌒
⌒
4
∠C, ∠D
∠A, ∠B
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,
∠B=30°,则∠ADC的度数为_______.
110°
小试牛刀
如图,等边三角形ABC内接于⊙O,连接OB,OC,那么∠BOC
的度数是( )
A.150° B.120°
C.90° D.60°
B
如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,
则∠B等于_____.
40°
小试牛刀
如图,AB是⊙O的弦,P在AB上,AB=10cm,PA=4cm,OP=
5cm,则⊙O的半径为( )
A.5 B.6 C.7 D.8
C
如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,
则∠BCD的度数为( )
A.40° B.50° C.60° D.70°
C
小试牛刀
如图: ,D、E分别是半径OA和OB的中点,求证:
CD=CE.
证明:连接OC.
在⊙O中,∵
∴∠AOC=∠BOC,
∵OA=OB,D、E分别是半径OA和OB的中点,∴OD=OE,
∵OC=OC(公共边),∴△COD≌△COE(SAS),
∴CD=CE(全等三角形的对应边相等).
课堂小结
课堂小结
“圆周角定理”是圆中的又一个重要定理,其作用在于转化同弧所对的圆心角与圆周角、同弧或等弧所对的圆周角之间的数量关系.在应用这一定理时,要注意“同弧、等弧”的前提条件,只有准确识别图形中角的位置关系,才能得到角之间的数量关系.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.3 圆心角与圆周角
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
什么是圆心角?它具有哪些性质?
新课精讲
探索新知
1
知识点
圆周角的定义
顶点在圆上,两边都与圆相交的角叫做圆周角.
如图,图(1)中∠APB是圆周角,图(2)和图(3)中 ∠AQB不是圆周角,图(4)中的∠ASB是圆周角,而∠ASC不是圆周角.
探索新知
如图所示,∠BAC是圆周角的是( )
例1
导引:顶点A必须在圆上,故排除D;AB , AC 必须分别与圆相交,B,C都不符合,故排除B,C .
A
探索新知
总 结
本题运用定义法和排除法,判断一个角是不是圆周角,必须抓住圆周角定义中的两个特征:
(1)角的顶点在圆周上;(2)角的两边都与圆相交.
典题精讲
下列四个图中,∠x为圆周角的是( )
C
探索新知
2
知识点
圆周角和圆心角的关系
如图,∠AOB和∠APB分别是 所对的圆心角和圆周角 .
(1)当点P在圆上按顺时针方向移动时(点P与点B不
重合),按照圆心O和圆周角的位置关系,可以分为几
种不同的情形?说出你的判断并画出相应的图形 .
(2)当圆心O落在∠APB的一条边上时,∠AOB与∠APB具有怎样的大小关系?说明理由 .
(3)当圆心O在的内部和外部时,(2)中的结论还成立吗?和同学进行交流 .
探索新知
通过探究,我们发现,当圆心O在∠ARB的一条边上时,如图 ,∠APB= ∠AOB .
∴ OP =OA,
∴∠OPA=∠OAP .
又∵∠AOB=∠OP A+∠OAP,
∴∠AOB=2∠APB,即∠APB= ∠AOB .
探索新知
对于圆心O在∠APB内部的情形,如图,连接PO并延长交⊙O于点D,
∵PD过圆心O,
∴∠APD = ∠AOD,∠BPD = ∠BOD .
∴∠APD+∠BPD= ∠AOD+ ∠BOD .
∴∠APB= ∠AOB .
探索新知
如图,对于圆心O在圆周角∠APB外部的情形,证明∠APB= ∠AOB .
做一做
结论
圆上一条弧所对的圆周角等于它所对的圆心角的一半 .
探索新知
例2 如图 ,点 A,B,C 均在⊙O 上,∠OAB = 46°. 求
∠ACB的度数 .
解:如图,连接OB .
∵OA=OB,
∴∠OAB=∠OBA .
∵∠OAB =46°,
∴∠AOB= 180°-2∠OAB=180°-2×46°= 88°.
∴∠ACB= ∠AOB= 44°.
探索新知
在同一个圆中,根据相等的弧所对的圆心角相等和圆上一条弧所对的圆周角等于它所对的圆心角的一半可知,若两条弧相等,则其中一条弧所对的圆心角等于另一条弧所对的圆周角的2倍.
总 结
典题精讲
1 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
A.60°
B.48°
C.30°
D.24°
D
典题精讲
将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB=______.
如图,BD是⊙O的直径,点A,C在⊙O上, ,∠AOB=60°,则∠BDC的度数是( )
A.60° B.45° C.35° D.30°
(第2题)
(第3题)
25°
D
探索新知
3
知识点
同弧或等弧与所对圆周角的关系
结合弧、弦、圆心角之间的关系定理和圆周角定理的推论可知:在同圆或等圆中,相等的圆周角所对的弧相等,所对的弦也相等,进而相等的弧所对的圆心角也相等.即在同圆或等圆中,圆周角、圆心角、弧、弦这四个量中有一组量相等,则可推出其他三组量相等,也称之为“四量关系定理”.
探索新知
例3 如图,在⊙O中, ,∠BAC=50°,则∠AEC的度数
为( )
A.65° B.75° C.50° D.55°
A
导引:由 ,可知∠ABC=∠ACB,已知
∠BAC=50°,故根据三角形内角和定理,可求出
∠ABC的度数,再根据“同弧所对的圆周角相等”,可得结果.
∵ ,∴∠ABC=∠ACB .
∵∠BAC=50°,∴∠ABC= ×(180°-50°)=65°.
∴∠AEC=∠ABC=65°,故选A .
探索新知
在一个圆中求一个圆周角的度数,可以从三个方面转化:
(1)转化为求该圆周角所对的弧所对的圆心角的度数;
(2)转化为求该圆周角所对的弧所对的其他圆周角的度数;
(3)转化为求与该圆周角所对的弧相等的弧所对的圆心角或圆周角的度数.
总 结
典题精讲
如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是 上一点,则∠APB的度数为( )
A.45° B.30° C.75° D.60°
D
典题精讲
如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=
75°,则∠B的度数是( )
A.15° B.25°
C.30° D.75°
如图,在⊙O中, ,∠AOB=40°,则∠ADC的度数是( )
A.40° B.30°
C.20° D.15°
C
C
学以致用
小试牛刀
如图所示,图中的圆周角共有______个,其中AB所对的圆周角是
___________,CD所对的圆周角是__________.
⌒
⌒
4
∠C, ∠D
∠A, ∠B
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,
∠B=30°,则∠ADC的度数为_______.
110°
小试牛刀
如图,等边三角形ABC内接于⊙O,连接OB,OC,那么∠BOC
的度数是( )
A.150° B.120°
C.90° D.60°
B
如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,
则∠B等于_____.
40°
小试牛刀
如图,AB是⊙O的弦,P在AB上,AB=10cm,PA=4cm,OP=
5cm,则⊙O的半径为( )
A.5 B.6 C.7 D.8
C
如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,
则∠BCD的度数为( )
A.40° B.50° C.60° D.70°
C
小试牛刀
如图: ,D、E分别是半径OA和OB的中点,求证:
CD=CE.
证明:连接OC.
在⊙O中,∵
∴∠AOC=∠BOC,
∵OA=OB,D、E分别是半径OA和OB的中点,∴OD=OE,
∵OC=OC(公共边),∴△COD≌△COE(SAS),
∴CD=CE(全等三角形的对应边相等).
课堂小结
课堂小结
“圆周角定理”是圆中的又一个重要定理,其作用在于转化同弧所对的圆心角与圆周角、同弧或等弧所对的圆周角之间的数量关系.在应用这一定理时,要注意“同弧、等弧”的前提条件,只有准确识别图形中角的位置关系,才能得到角之间的数量关系.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
